ДЕФИЦИТНАЯ МОДЕЛЬ ФИНАНСОВОГО ВЗАИМОДЕЙСТВИЯ ПРЕДПРИЯТИЙ В РЕГИОНАХ

Вступление. Социально-экономическое развитие регионов является основой для повышения жизненного уровня населения. Необходимым условием реализации программы социально-экономического развития является эффективное и прозрачное использование бюджетных средств, возможность контроля процесса расходов, особенно при выполнении региональных бюджетных и совместимых с инвесторами проектов. Последнее создает условия для привлечения инвестиций в регионы. Поэтому исследования экономико-математической модели поэтапного распределения средств между соисполнителями региональных проектов и контроля за их выполнением является актуальным и представляет существенный интерес, особенно для органов местного самоуправления при планировании основных расходов в пределах регионов.

Анализ последних исследований и публикаций. Финансовая взаимодействие структурных единиц предприятий, корпораций, регионов рассматривалась многими учеными [2-9]. Их исследования были сосредоточены на определении эффективных методов планирования и управления денежными потоками, их оптимизации и согласованности, что должно обеспечить финансовую стабильность, рост финансового потенциала предприятий, дальнейшее их развитие, созданию привлекательных условий для инвестиций. Математические методы и модели, применяемые в исследованиях денежных потоков предприятий и между ними, освещены в работах [10-14].

Нерешенные части проблемы. В работах [10-11,14] на основе вероятностного подхода – использование теории цепей Маркова было проведено исследование по финансовой взаимодействия между организациями (региональными структурами, торговыми партнерами). Во-первых, рассматривалась бездефицитная замкнутая модель, без определения условий взаимодействия с другими системами. Во-вторых, формула, которая описывает состояние системы на каждом шагу дефицитной модели, имеет сложный вид, который не позволяет проведение быстрого аналитического анализа.

Постановка задачи. Целью исследования является нахождение (при использовании метода z – преобразование) аналитического вида дефицитной модели денежно-товарных потоков между структурными единицами выбранной системы а также выявление условий для открытости системы и текущих величин денежных потоков между выбранной и другими внешними системами.

Основные результаты исследования. Для городских бюджетов выгодным является расходование всех средств на реализацию инвестиционных проектов, региональных программ на территории региона или в виде поддержки отечественного регионального производителя путем целевых закупок. Бездефицитное для исполнителей завершения проекта не всегда возможно, если все средства остаются в пределах региона. Рассмотрим региональную систему, которая состоит из структурных единиц, между которыми проходят финансовые операции (денежно-товарные потоки). Общий процесс товарно-денежного обмена между единицами через определенный промежуток времени (шаг) может быть представлен следующим модельным рекуррентным уравнением с матрицей переходных вероятностей для эргодической цепей Маркова:

(1)

где - вектор распределения финансовых ресурсов между единицами после k шага, -начальный вектор распределения финансовых ресурсов.

Матрицы  и и будем называть матрицами получения и расходования средств соответственно [10], которые определяют векторы распределения получения и расходования финансовых ресурсов между единицами после шага .

Для аналитического изучения поведения цепей Маркова к переходу в стационарное состояние применяем метод z-преобразований к уравнению (1), при котором  переходит к

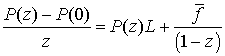(2)

После очевидных преобразований уравнение (2) принимает вид:

(3)

где - единичная матрица размера , а - обратная матрица к матрице

Обозначим через обратное преобразование матрицы и представим эту матрицу в виде суммы слагаемых:

(4)

где стохастическая матрица, которая соответствует члену матрицы с множителем

Утверждение о стохастичность эквивалентно тому, что определитель матрицы равна нулю при . Стохастическая матрица всегда имеет хотя бы одно собственное значение, равное единице. Более того, строки матрицы будут равны друг другу и составлять компоненты вектора предельных (стационарных) вероятностей состояния системы. Матрицу называют стационарной матрицей.

Составляющие матрицы , которые остались и обозначены через  , определяют переходную ее составляющую, так как описывают поведение цепи Маркова в переходный период из состояния в состояние.

Диагональные элементы матриц  и пропорциональны долям финансовых ресурсов, структурные единицы оставляют у себя при переходе из одного состояния в другое на соответствующие операции. Абсолютной величине этих ресурсов, которую можно планировать -единицы для взаимодействия с внешними структурами, можно определить по формулам:

(5)

где , – -компоненты векторов ,ответ, – диагональные элементы стационарных матриц .

Рассмотрим на конкретном примере, как при помощи z-преобразования получить аналитический вид распределения финансовыми потоками (получения, расходы) между региональными структурными единицами.

Пусть матрицы  и и их произведения имеют вид:

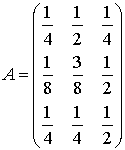(6)

(7)

(8)

Построим для матрицы матрицу

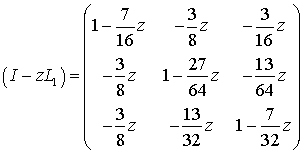(9)

Определитель этой матрицы равен:

(10)

а обратная к ней матрица имеет вид:

Обратное преобразования матрицы – определяет произведение матриц

где

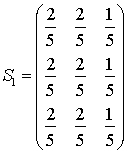(11)

Построим для матрицы матрицу

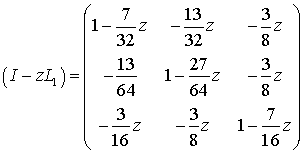(12)

Определитель этой матрицы и обратная к ней матрица имеют вид:

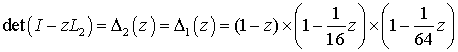(13)

Обратное z преобразования матрицы определяет произведение матриц

где
Таким образом, методом z-преобразования определенные матрицы получения и расходования средств исполнителями проекта на каждом этапе (шаге) исполнения. Матрицы и показывают соответствующие предельные состояния распределения средств. С помощью произведений векторов начальных состояний и диагональных элементов матриц и определяются финансовые ресурсы, которые исполнители могут использовать в течение шага с внешними партнерами при сохранении значений произведений перед следующим шагом.

Выводы. Таким образом, предложенный метод z-преобразований позволяет благодаря установленной аналитический форме без использования компьютерной техники знать распределение общего бюджета между партнерами на каждом шагу эргодического цепи Маркова и определить время совпадения процесса к стационарному состоянию. Это позволяет контролировать процесс выполнения проекта, в частности процесс его финансирования, на каждом этапе и при необходимости, когда возникают проблемы, менять правила распределения, то есть матрицы .

1. Полтерович В. М. Институты догоняющего развития (к проекту новой модели экономического развития России) // Экономические и социальные перемены: факты, тенденции, прогноз. № 5. С. 34—56.
2. Бланк И. А. Финансовый менеджмент: учебник / И. А. Бланк. – М.: Ника-Центр, Эльга, 2002. – 512 с.
3. Бочаров В. В. Управление денежным оборотом предприятий и корпораций / В. Бочаров. – М.: Финансы и статистика, 2002. – 144 с.
4. Синцова Е.А. Формирование денежных потоков промышленного предприятия в условиях инфляции : Дис. … канд. экон. наук. — СПб., 2002.
5. Бланк И.А. Управление финансовыми ресурсами / М.: Издательство «Омега-Л»: ООО «Эльга», 2011. – 786 с
6. Покровский Ю. Н. Методика анализа чистого денежного потока в условиях дефицита денежных средств / А. С. Кокин, Н. Ю. Покровский // Аудит и финансовый анализ. – 2010. – № 3. – С. 144-148.
7. Ермасова И.Б. Управление денежными потоками компании. / И.Б. Ермасова. – М.: БДЦ-пресс, 2013. – с.52.
8. Тимофеева Т. В. Анализ денежных потоков предприятия / Т. В. Тимофеева. – М.: Финансы и статистика; ИНФРА-М, 2010. – 368 с.
9. Коновалова А.В. Анализ денежных потоков /учебное пособие / Ярославский государственный университет им. П. Г. Демидова. Ярославль, 2015. – 108 с.
10. Хэлдман Ким Управление проектами. Быстрый старт / Ким Хелдман; Пер. с англ. Шпаковой Ю.; Под ред. Неизвестного С. И. – М.: ДМК Пресс; Академия АйТи, 2008. – 352 с.
11. Турманидзе Т.У. Анализ и оценка эффективности инвестиций : учебник / Т.У. Турманидзе. Москва : ЮНИТИ-ДАНА, 2015. 247 с.
12. Корнийчук М.Т. Риск и надежность. Экономико-стохастические методы и алгоритмы построения и оптимизации систем: Монография. / М. Т. Корнийчук, И. К. Совтус – М .: Финансы, 2000.- 212 с.
13. Витлинський В.В. Риск в менеджменте. / В. Витлинський, С. И. Наконечный – М .: Борисфен, 1996. – 330 с.
14. Жлуктенко В.И., Наконечный С.И., Савина С.С. стохастические процессы и модели в экономике, социологии, экологии: Учеб. пособие. / В. И. Жлуктенко, С. И. Наконечный, С. С. Савина – М .: Финансы, 2002. – 226 с.
15. Ховард Р. А. Динамическое программирование и марковские процессы / Р.А. Ховард. – М .: «Советское радио», 1964. – 195с.

Все статьи автора «Бадекин Максим Юрьевич»