Постановка проблемы. Вероятностное моделирование совокупностей объектов является одним из важных направлений использования теории марковских процессов. Она включает, в частности, такие области экономики, как управление воспроизведением парков производственного оборудования [1, 2], распространение инноваций [3], теорию конкуренции [3]. Также вероятностное моделирование может быть полезным для руководства в процессе перспективного планирования замены устаревшего оборудования предприятия.
Анализ последних исследований и публикаций. Сегодня проблемы, связанные с моделированием и оптимизацией управления заменой производственного оборудования с учетом только его физического износа, исследованы достаточно полно [1, 2]. Об учете возможности замены морально устаревшего оборудования вместе с физически изношенным, то преимущественно используются детерминированные нелинейные динамические модели, заимствованные из математической биологии. Однако указанный математический аппарат не является достаточно гибким для того, чтобы учесть важные детали процесса воспроизводства реальных парков производственного оборудования. В частности, с его помощью очень трудно (если вообще возможно) описать совместную динамику воспроизводства парка оборудования и результатов его работы, включая реализацию продукции на рынке.
Указанных недостатков в значительной мере лишен подход, основанный на использовании различных типов марковских случайных процессов.
Постановка целей. Эта работа рассматривает построение и анализ стохастической модели воспроизводства парка машин производственного назначения, которая учитывает одновременно их физический и моральный износ, а также использования аппарата марковских случайных процессов.
Изложение основного материала. Рассмотрим парк машин одного производственного назначения в составе какого-то предприятия, причем все машины принадлежат только к одной из двух категорий: старого образца (старая модель) и нового образца (новая модель). Парк может пополняться группами машин обеих моделей, при этом в моменты поступления групп машин новой модели могут списываться несколько машин старого образца. Кроме того, машины обеих моделей могут списываться в случайные моменты времени в результате их физического износа.
Обозначим через 
количество машин старой (новой) модели, находящихся в эксплуатации в парке в момент времени 
. Примем следующие допущения о возможности изменения состояния процесса 
в малом интервале времени 
:
а) за время 
парк пополнится 
машинами старой модели с вероятностью
где 
- интенсивность потока групп машин, прибывающих; 
- вероятность того, что прибыла группа состоит ровно из 
машин;
б) за время 
парк пополнится 
машинами новой модели и одновременно будут списаны 
машин старой модели с вероятностью
где 
- интенсивность потока машин новой модели, прибывающих; 
- вероятность того, что группа машин новой модели, пополняет парк состоит из 
единиц машин, и одновременно с пополнением списывается ровно 
машин старой модели;
в) время 
будет списана одна машина старой (новой) модели в связи с его физическим износом из числа 
(соответственно 
), находящихся в парке в момент 
, с вероятностью
где 
- средний срок службы одной машины старой (новой) модели до полного физического износа)
г) вероятность того, что за время 
не произойдет изменения состояний процесса 
, равно
Через допущения (а-г) процесс 
является однородным, марковским.
Обозначим
Обычным методом для нахождения этих вероятностей можно вывести такую бесконечную систему прямых дифференциальных уравнений Колмогорова:
 |
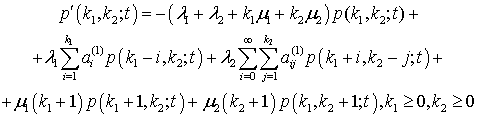(1) |
Введенные вероятности должны также удовлетворять условию нормирования:
 |
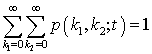(2) |
В частности, если машины старой модели поступают, то они образуют постоянную группу размера n, а машины новой модели – группу размера m, причем во время ее поступления списывается всегда 
машин старой модели, то в (1) следует положить
Для практического использования уравнений (1), (2) удобнее ограничить их количество, сделав систему (1) конечной. Можно считать, например, что она справедлива только тех значений 
и 
, которые удовлетворяют условию
где 
- производительность одной машины старой (новой) модели; 
- общая производительность парка машин (она определяется рыночным спросом на производимую продукцию парком).
Пусть 
означает суточные эксплуатационные расходы для одной машины старой (новой) модели. Естественно считать, что выполняются следующие условия:
причем хотя бы одно из них выполнялось как строгое неравенство.
В то же время стоимость одной новой машины новой модели
и должна быть больше стоимости новой машины старой модели 
, т. е.
С помощью этих рассуждений можно сформулировать задачу оптимального управления воспроизведением парке: нужно найти такие значения целочисленных параметров 
которые максимизируют средний доход за единицу времени, получается предприятием от продажи производимой парком продукции, то есть выражение
где 
- цена единицы продукции, вырабатываемой парком; 
- продажная цена списанной в результате физического износа одной машины старой (новой) модели; 
- стационарное математическое ожидание числа машин старой (новой) модели, находящихся в эксплуатации, то есть
, 
предельные вероятности состояний процесса 
, определяемые путем решения системы алгебраических уравнений, следует из (1), (2) по 
. Для нахождения вероятностного распределения 
можно использовать матричный метод, вроде того, который использовался в [2].
Выводы. Итак, аппарат марковских процессов позволяет формализовать достаточно сложные реальные процессы, связанные с учетом замены производственного оборудования (в долгосрочном планировании), не только его физического износа, но и возможности замены оборудования совершенной техникой.
Перспективы дальнейших исследований представляет интерес обобщение приведенной стохастической модели в нескольких направлениях, например, в случае:
- детального описания процесса физического старения машин (см. [1]);
- переменных режимов работы парка;
- случайного колебания рыночного спроса на производимую продукцию и соответствующего колебания численности парка машин.
Библиографический список
- Баранов Д.А. Сроки амортизации и обновления основных производственных фондов: вопросы теории и методологии. М.: Наука, 1977. 157 с.
- Ширяева Л.В. Методы и модели управления воспроизводством парков оборудования. Вероятностный подход / Л.В. Ширяева. – Одесса: Астропринт, 2008. – 256 с.
- Сахал Д. Технический прогресс: концепции, модели, оценки / пер. с англ. / Д. Сахал. – М.: Финансы и статистика, 1985. – 360 с. 4. Баруча-Рид А.Т. Элементы теории марковских процессов и их приложения / пер. с англ. / А.Т. Баруча-Рид. – М.: Наука, 1969. – 511 с.
Количество просмотров публикации: Please wait