ЭМПИРИЧЕСКАЯ МОДЕЛЬ ПОВЕРХНОСТИ ТВЕРДЫХ ТЕЛ

Введение

Важной особенностью развития современных технологий является учет влияния поверхностей и приповерхностных слоев на различные свойства материалов. Это особенно важно для объектов с характерными размерами нанометрового масштаба [1-3]. Для изучения структуры и свойств поверхности твердых тел используется множество разнообразных методов. Каждый метод характеризуется глубиной исследуемого слоя и характером получаемых сведений. Методы в соответствии с монографией [2] можно разделить на следующие группы:
- дифракционные, где информацию о структуре поверхности получают, анализируя электроны или кванты упруго рассеянные кристаллом. Наиболее распространенными методами из этой группы являются: дифракция медленных электронов (ДМЭ), рентгеновская дифракция под скользящими углами. В основе ДМЭ лежит анализ углового распределения упруго отраженных электронов при энергии первичного пучка E_p<300 эВ. Высокая чувствительность метода ДМЭ к структуре поверхности обусловлена в первую очередь тем, что длина свободного пробега медленных электронов до неупругого рассеяния мала (λ=10 Е), т.е. электрон, проникший на глубину более 5 Еот поверхности имеет мало шансов возвратиться в вакуум без потерь энергии и дать вклад в дифракционную картину. Следовательно, в формировании картины ДМЭ принимают участие только ближайшие к поверхности слои атомов [4]. Основная идея второго метода заключается в том, что оптимальное соотношение «сигнал-шум» достигается при скользящем падении рентгеновского излучения, когда угол падения равен или меньше критического угла полного внутреннего отражения. Когда угол падения становится меньше критического, преломленная волна экспоненциально затухает в объеме на характерной глубине порядка нескольких десятков ангстрем (например, для кремния эта глубина 32 Е, а для золота 12 Е). В результате формируется, так называемая, исчезающая волна, которая распространяется параллельно поверхности. Поэтому дифракция таких волн дает информацию о структуре поверхностного слоя [2];
- методы электронной спектроскопии. К методам из этой группы относятся: электронная оже-спектроскопия (ЭОС), спектроскопия характеристических потерь энергии электронами (СПЭ), фотоэлектронная спектроскопия (РФЭС). Толщина слоя, состав которого определяется методом ЭОС, соответствует средней длине свободного пробега (глубина выхода) оже-электронов. Глубина меняется от ~0,5 нм (при энергии 50 эВ) до ~2 нм (при энергии оже-электронов 500 эВ) [5]. Глубина разрешения метода СПЭ примерно составляет 1 нм [6]. РФЭС характеризует поверхностный слой образца толщиной до 10 нм. Толщина анализируемого слоя определяется длиной свободного пробега электронов и составляет (0.5-2.5) нм для металлов и (4-10) нм – для органических и некоторых полимерных материалов [6];
- методы, основанные на зондировании исследуемой поверхности ионами различных энергий. Это спектроскопия ионного рассеяния (СИР) и вторичная ионная масс-спектрометрия (ВИМС). Чувствительность метода СИР к поверхностным слоям обусловлена большим сечением рассеяния (порядка 1 Е), поэтому ионы не могут проникать на глубину большую нескольких атомных слоев. Метод СИР применяется в основном для определения состава и структуры поверхности [7]. При методе ВИМС анализируется не поверхность образца, как при других методах, а распыленное вещество. Толщина анализируемого слоя в методе ВИМС зависит от энергии первичных ионов и достигает ~5 нм [7];
- методы, которые служат для получения увеличенных изображений поверхности: метод нарушенного полного внутреннего отражения (НПВО), просвечивающая электронная микроскопия (ПЭМ), сканирующая электронная микроскопия (СЭМ), сканирующая туннельная микроскопия (СТМ), атомно-силовая микроскопия (АСМ). Глубина метода НПВО зависит от коэффициента поглощения исследуемого материала и составляет для высокомолекулярных твердых тел примерно ~1 мкм [8]. Существенным ограничением для наблюдения в ПЭМ является толщина объекта, которая не может превышать 100 нм, а обычно составляет от 20 нм до 30 нм [9]. СЭМ применяется для изучения морфологии надмолекулярных образований в кристаллических и аморфных полимерах [10]. В методе СТМ острие подводится к поверхности на расстояние 10 Е, то при приложении между острием и образцом небольшого (от 0,01 В до 10 В) напряжения смещения через вакуумный промежуток начинает протекать туннельный ток порядка 10^-9 А и картина поверхностной структуры получается на атомном уровне [11]. В методе АСМ рельеф исследуемой поверхности формируется, как правило, либо в режиме постоянной высоты, либо в режиме постоянной силы. В первом случае кантилевер передвигается в горизонтальной плоскости, и регистрируется его отклонение в каждой точке. Во втором случае, с помощью системы обратных связей постоянным поддерживается отклонение (прогиб) кантилевера, т.е. сила взаимодействия его с образцом [12].
Эмпирическая модель поверхности твердых тел
В работах [13, 14] обобщена предложенная нами модель поверхностного слоя атомарно-гладких металлов. Схематически эта модель представлена на рисунке 1.

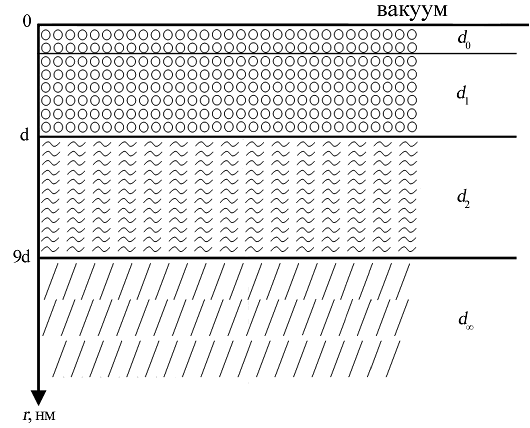
d₀ - слой де Бройля; d₁ - слой d(I); d₂ – слой d(II); d₈ - слой массивного образца
Рисунок 1 – Схематическое изображение поверхностного слоя

Слой де Бройля d₀=λ_дБ=h/p для металлов составляет от 0,01 нм до 0,1 нм. В этом слое проявляются размерные эффекты в квантовом случае, к которым причисляют электронный двумерный газ (пленки, гетероструктуры и т.д.); квантовые проволоки или квантовые нити, которые относятся к одномерному электронному газу; квантовые точки, которые относятся к нульмерному электронному газу [15]. Для определения толщины поверхностного слоя различных соединений нами использовалась зависимость физического свойства от размера A(r). Слой d(I)=d описывается зависимостью: (1)В слое d(I) с атомами чистых металлов происходит реконструкция и релаксация, связанная с перестройкой поверхности [16]. Для золота постоянная решетки равна d(I) = 0.41 нм и поверхность перестраивается на расстоянии (d(I)_Au=1.2/0.41˜3) трех атомных монослоев. Размерные эффекты в слое d(I) определяются всем коллективом атомов в системе (коллективные процессы). Такие «квазиклассические» размерные эффекты наблюдаются только в наночастицах и наноструктурах [17].
Слой d(II) описывается зависимостью:
 (2)
Параметр d связан с поверхностным натяжением s формулой:
. (3)
Здесь s – поверхностное натяжение массивного образца; υ – объем одного моля; R – газовая постоянная; T – температура. В [13], показано, что с точностью до 3% выполняется:
. (4)
где T_m – температура плавления твердого тела (К). Соотношение выполняется для всех металлов и для других кристаллических соединений. При T=T_m получим:
. (5)
Уравнение (5) показывает, что толщина поверхностного слоя d(I) определяется одним фундаментальным параметром – молярным (атомным) объемом элемента (υ=M/ρ, M – молярная масса (г/моль), ρ– плотность (г/см³)), который периодически изменяется в соответствие с таблицей Д.И. Менделеева.
Слой d(II) простирается примерно до размера d(II)˜10d=d₈, где начинается объемная фаза. С этого размера начинаются размерные свойства. Под наноматериалами принято понимать материалы, основные структурные элементы которых не превышают нанотехнологической границы ~100 нм, по крайней мере, в одном направлении [18]. Многие исследователи считают, что наноструктуры обладают критической величиной, которая связана с характерным размером их элемента – или это длинна свободного пробега носителей заряда, или это длина доменных стенок и тому подобное [17]. Это означает, что в слое d(II) наблюдаются многочисленные размерные свойства, обусловленные оптикой, электричеством, магнетизмом, механикой и другими свойствами в соответствии с уравнением (2).
Атомарно-гладкие металлы
Переходные элементы в таблице Менделеева разделяют на d-элементы, 4f-элементы (лантаноиды) и 5f-элементы (актиноиды) [19]. Все эти три группы химических элементов различаются по заполнению nd-орбиталей. Например, d-орбитали простираются за пределы атома слишком далеко и потому их электроны существенно взаимодействуют с электронами окружения. Это приводит к тому, что np-орбитали электронов атома образуют c ns- и (n-1)d- орбиталями прочные химические связи. Эти химические связи образуют особую природу переходных элементов.
В таблице 1 приведена толщина поверхностного слоя d–металлов, рассчитанная по уравнению (5) около температуры плавления (за исключением атомов 7 периода).

Таблица 1 – Толщина поверхностного слоя d – металлов (Ме-металл)

Все размеры d(I) имеют значения около 2 нм (исключая иттрий и скандий). Толщина поверхностного слоя для золота, определенная методом скользящих рентгеновских лучей, оказалась равной 1.2 нм [2]. С учетом коэффициента теплового расширения золота эта величина совпадает с таблицей 1. В таблице 2 толщина слоя d(I) приведена для лантаноидов.

Таблица 2 – Толщина поверхностного слоя d(I) лантаноидов

Здесь наблюдаются значения от 4 нм до 5,5 нм, что в два раза больше толщин слоя для d-элементов. Именно поэтому f–элементы не образуют высокоэнтропийных сплавов.
Толщина поверхностного слоя типичных полупроводников
В таблице 3 представлены слои d(I) полупроводников.

Таблица 3 – Толщина поверхностного слоя полупроводников (ПП)

В слое d(I) происходит реконструкция поверхности [2, 20], меняется на обратный эффект Холла-Петча [21] и другие физические эффекты. Монокристаллический кремний имеет атомную (молярную) массу М = 28.086 (г/моль), плотность ρ = 2.33 (г/см³) и параметр решетки (кубическая, алмазная) а = 0.54307 нм. Тогда из уравнении (5) следует:
 (6)
Эту толщину экспериментально можно определить с помощью скользящих рентгеновских лучей в режиме полного внутреннего отражения. В работе [22] это величина составила ~2 нм, что почти совпадает с (6). Это подтверждает уравнение (5). Итак, слой d(I)_Si атомарно-гладкого монокристаллического кремния представляет собой наноструктуру. Число частиц кремния в монослое равно n=d(I)_Si/a˜4 (a – постоянная решетки). То есть слой d(I)_Si содержит 4 атомные плоскости кремния. А d(II)_Si ˜ 21 нм представляет наноструктуру по Глейтеру [23]. Толщина де Бройля кремния равна d₀ = 0.116 нм.
Международный союз по химии IUPAC принял номенклатуру, согласно которой диаметр размер пор подразделяется на: микропористый <2 нм, мезопористый (2-50) нм и макропористый >50 нм [24].
Важной характеристикой p-Si является степень его пористости P, определяемая как:  (7)
где ρ_ПК – плотность пористого кремния (ПК), ρ_Si – плотность монокристалла.
Если подставить уравнение (7) в уравнение (5), то получим:

 (8)

Типичное значение пористости кремния имеет значение (40-70)%, а при сверхкритическом высушивании [25] достигает 95%. Из уравнения (8) вытекает следующая таблица 4.

Таблица 4 – Толщина поверхностного слоя кремния при различных значениях пористости

Таблица 4 показывает, что пористость кремния существенно влияет на свойства наноструктур. Это было также показано в работе [22], но там не приводились количественные данные (как в таблице 4) из-за сложности проведения экспериментов.
Таблица 4 показывает, что, начиная с пористости 80%, кремний по своим свойствам слоя d(II)_Si выходит за наноструктуру по Глейтеру [23]. Для большинства чистых металлов толщина поверхностного слоя d(I) не превышает 3 нм (для d(II)~30 нм). В таблице 5 приведены значения толщин соединений кремния, определенные по формуле (5). Из таблицы 5 следует, что толщина поверхностного слоя d(I) не превышает (3-6) нм (за исключением 4 силицидов).

Таблица 5 – Толщина поверхностного слоя соединений кремния [26]

В работе [27] проведены расчеты из первых принципов силицидов Cr₅Si₃. Показана их значительная химическая стойкость к окислению при высоких температурах. Нанопроволоки  перспективны для фотоэлектрических и полевых эмиттеров. В работе [28] проведены расчеты . Показана очень высокая твердость этих силицидов. В работе [29] показано, что силициды  обладают необычайными физико-механическими свойствами и демонстрируют большие возможности применения их в качестве высокотемпературных легких материалов для турбинных лопаток, теплозащитных плит для камер сгорания и ракетных форсунок. Модуль Юнга и температура Дебая тоже оказываются значительными.
Ниобий-силицидные сплавы на основе Nb₅Si₃ обладают высоким возможностями из-за высокой температуры плавления (2527 К) и низкой плотности (7.1 г/см³). Поэтому эти сплавы могут быть хорошими кандидатами для использования их при температурах выше 1473 К в качестве замены Ni-суперсплавов с максимальной температурой около 1273 K [30].
В таблице 5 приводятся 4 сложных силицида, имеющих толщину слоя d(II) >100 нм, как и у пористого кремния. Эти силициды обладают необычайными свойствами, как и пористый кремний. Это наталкивает на мысль, что получение наноструктур с заданной пористостью открывает перспективу создания новых солнечных батарей, микротопливных элементов, суперконденсаторов, эффективных мембран и новых применений в медицине.

Толщина поверхностного слоя сложных кристаллических структур
По данным ряда исследователей стелс-покрытие – это слои оксидов металлов толщиной (70-90) нм. Кроме того, что покрытие делает самолет менее заметным, оно защищает летчиков от воздействия ультрафиолета. В таблице 6 приведен пример стелс-покрытия.

Таблица 6 – Толщина поверхностного слоя оксида металла

Из таблицы 6 видно, что слои оксидов металлов в виде минералов толщиной (70-90) нм наблюдаются довольно редко (хлормайенит). Но возможно синтезировать такие соединения. При r=d в поверхностном слое происходит фазовый переход, что и приводит к стелс-эффекту.
Толщина поверхностного слоя полимеров
Из полимеров мы рассмотрим арены или ароматические углеводороды –соединения, молекулы которых содержат устойчивые циклические группы атомов (бензольные ядра) с замкнутой системой сопряженных связей с симметрией D_2h (нафталин, антрацен, тетрацен, пентацен) и другой молекулярной симметрией (кононены, фуллерены). Толщина поверхностного слоя этих полимеров представлена в таблице 7.

Таблица 7 – Толщина поверхностного слоя полимеров

Сравнение таблицы 7 с таблицей 1 показывает, что толщина поверхностного слоя большей части металлов на один или два порядка меньше, чем у полимеров. Именно поэтому, полимеры с наночастицами железа сферической формы используют в качестве присадок моторных масел двигателей внутреннего сгорания [31]. Многие нанопорошки в полимерах стали использоваться в нано- и микроэлектронике [32].

Толщина поверхностного слоя аморфных твердых тел
Как можно рассматривать аморфные твердые тела с присущим им беспорядком? Как систему атомов с вероятностным их распределением, которое оказывается не произвольным. На эту атомную систему есть свои ограничения [33]. Из-за того, что эти системы являются конденсированными системами, то аморфные тела имеют структуры, которые близки к плотной упаковке. У них нет симметрии Вороного, но ячейка Вигнера-Зейтца имеет приблизительно тот же объем и число ближайших соседей такое же, как и у упорядоченных кристаллов. Плотность аморфных тел примерно такая же, как у конденсированных сред.
Было обнаружено, что неупорядоченные вещества проявляют линейную зависимость удельной теплоемкости и квадратичную зависимость теплопроводности от температуры, в отличие от кубической зависимости для обеих характеристик в кристаллах (см., напр., [33]). Позже в исследованиях, проведенных при очень низких температурах, были обнаружены аномалии в поглощении ультразвука и электромагнитного излучения, нелинейные эффекты типа насыщения поглощения и многие другие необычные явления в поведении неупорядоченных веществ (см., напр., [33]). Оказалось также, что указанные аномальные свойства носят универсальный характер и практически не зависят от конкретного состава и структуры вещества. Эти наблюдения явно указывали на то, что наблюдаемые аномальные свойства неупорядоченных сред обусловлены не конкретным строением изучаемого вещества, а самим фактом наличия беспорядка во внутренней структуре таких сред.
В таблице 8 показана толщина поверхностного слоя аморфного сплава. Аморфные магнитомягкие металлические сплавы обладают такими уникальными свойствами, как высокая магнитная проницаемость, низкая коэрцитивная сила и не зависящая от температуры электропроводность [34].

Таблица 8 – Толщина поверхностного слоя аморфного сплава

Из таблицы 8 следует (и для других сплавов тоже), что толщина поверхностного слоя аморфного сплава не превышает 2 нм.

Толщина поверхностного слоя металлических стекол
Металлические стекла обычно получают при закалке из жидкого состояния со скоростями охлаждения ~5·10⁴-10⁷ К/c, поэтому образуются изотропные, однородные системы из атомов [35]. Этим они отличатся от полимеров и оксидных стекол. В полимерах структура состоит из длинных молекул. В оксидных стеклах металлические и кислородные атомы связаны настолько жестко, что образуется ограниченная структура.
Таблица 9 – Толщина поверхностного слоя металлических стекол

В таблице 9 приведена толщина поверхностного слоя металлических стекол. Данные, перечисленные в столбцах 1-3, взяты из работы [35].
Из таблицы 9 следует, что толщина поверхностного слоя металлических стекол не превышает 1 нм. Этим они не сильно отличаются от аморфных сплавов.
Заключение
В заключение подчеркнем, что толщина поверхностного слоя d(I) атомно-гладких тел определяется одним фундаментальным параметром – молекулярным (атомным) объемом твердого тела, который отличен для металлов, аморфных твердых тел, стекол, полимеров и т.д. Глубокая причина такой закономерности не вполне понятна и требует дальнейших исследований.

1. А.И. Гусев, А.А. Ремпель. Нанокристаллические материалы. – М.: Физматлит. 2000. – 224 с.
2. К. Оура, В.Г. Лифшиц, А.А. Саранин, А.В. Зотов, М. Катаяма. Введение в физику поверхности. М.: Наука. 2006. – 490 с.
3. М.В. Мамонова, В.В. Прудников, И.А Прудникова. Физика поверхности. Теоретические модели и экспериментальные методы. – М.: Физматлит. 2011. – 400 с.
4. В.Ф. Киселев, С.Н. Козлов, А.В. Зотеев. Основы физики поверхности твердого тела. – М.: изд-во Московского университета. 1999. – 284 с.
5. Л. Фелдман, Д. Майер. Основы анализа поверхности и тонких пленок. – М.: Мир. 1989. – 344 с.
6. Д.Д. Карамов, В.М. Корнилов, А.Н. Лачинов, В.А. Крайкин, И.А. Ионов. // ЖТФ, 2016. -Т.86. -В.7. -С. 124-129.
7. М. Праттон. Введение в физику поверхности. – Ижевск: НИЦ «Регулярная и хаотическая динамика». 2000. – 256 с.
8. П. Пейтнер, М. Коулмен, Дж. Кениг. Теория колебательной спектроскопии. Приложение к полимерным материалам. – М.: Мир. 1986. – 580 с.
9. Д. Брандон, У. Каплан. Микроструктура материалов. Методы исследования и контроля. – М.: Техносфера. 2004. – 384 с.
10. Москвина М.А., Трофимчук Е.С. Получение и свойства гибридных полимер-неорганических нанокомпозитов. – Москва, МГУ им. М.В. Ломоносова, 2017. – 118 с.
11. В. Л. Миронов. Основы сканирующей зондовой микроскопии. Российская академия наук, Институт физики микроструктур. г. Нижний Новгород, 2004 г. – 110 с.
12. Витязь П.А., Свидунович Н.А., Куис Д.В. Наноматериаловедение. – Минск: Вышэйшая школа, 2015. – 512 с.
13. Юров В.М., Гученко С.А., Лауринас В.Ч. // Физико-химические аспекты изучения кластеров, наноструктур и наноматериалов. 2018.? Вып. 10. – С. 691-699.
14. Юров В.М., Лауринас В.Ч., Гученко С.А. // Нано- и микросистемная техника, 2019, №6. – С. 347-352.
15. Арутюнов К.Ю. // ДАН ВШ РАН. 2015. №3(28). – С. 7-16.
16. Владимиров Г.Г. Физика поверхности твердых тел. – СПб.: Лань, 2016. – 352 с.
17. Уваров Н.Ф., Болдырев В.В. // Успехи химии. 2001. Т. 70(4).–С. 307-329.
18. Гусев А.И., Ремпель А.А. Нанокристаллические материалы. – М.: Физматлит, 2000. – 224 с.
19. Голованова О.А. Химия металлов. – Омск: Изд-во Ом. гос. ун-та, 2015. – 552 с.
20. Ищенко А.А., Фетисов Г.В., Асланов Л.А. Нанокремний: свойства, получение, применение, методы исследования и контроля. – М.: Физматлит, 2011. – 648 с.
21. Юров В.М. // Вестник КарГУ. Физика, 2013, № 3 (71). – С. 56-61.
22. Балагуров Л.А., Павлов В.Ф., Петрова Е.А., Боронина Г.П.. // ФТП, 1997, том 31, № 8. – С. 957-960.
23. Gleiter H. Nanostructured materials: basic concepts and microstructure // Acta mater., 2000. V.48. – P. 1-29
24. Korotcenkov G. Porous Silicon: From Formation to Application: Formation and Properties, Vol. 1, CRC Press, 2015. – 423 p.
25. Lehmann V., Ronnebeck S. // Journal of The Electrochemical Society, 1999, V. 146, №. 8. – P. 2968-2975.
26. Yurov V.M., Eremin E.N., Guchenko S.A., Laurinas V.Ch. // Cite as: AIP Conference Proceedings 2141, 040023 (2019); https://doi.org/10.1063/1.5122142
27. Ren B., Lu D.H., Zhou R., Ji D.P., Hu M.Y. and Feng J. // Chin. Phys. B. 2018, Vol. 27, No. 10. – P. 107102-1 – 107102-11
28. Wan B., Xiao F., Y. Zhang et al. // Journal of Alloys and Compounds, 2016, Vol. 681. – P. 412-420.
29. Kishida K., Fujiwara M., Adach H. et al. // Acta Materialia, 2010, Vol. 58, № 3. – P. 846-857.
30. Kim W.Y., Yeo I.D., Kim M.S. and Hanada S. // Materials Transactions, 2002, Vol. 43, No. 12. – P. 3254-326
31. Белевитин В.А. Материаловедение: неметаллические материалы. – Челябинск: Изд-во Юж.-Урал. гос. гуман.-пед. ун-та, 2017. – 143 с.
32. Мусихин С.Ф., Ильин В.И.. Гибридные полимер-полупроводниковые наноструктуры, технология, приборы. Научно-технические ведомости СПбГПУ, 2007, Т.4(10). – С. 105-112.
33. Дегтяренко Н.Н. Введение в физику неупорядоченных конденсированных систем. – М.: НИЯУ МИФИ, 2011. – 228 c.
34. Стародубцев Ю.H., Безозеров В.Я. Магнитные свойства аморфных и нанокристаллических сплавов. – Екатеринбург: Изд-во УрГУ, 2002. – 384 с.
35. Абросимова Г.Е. Эволюция структуры металлических стекол при внешних воздействиях. – Дисс. доктора физ.-мат. наук, Черноголовка, 2012. – 296 с.

Все статьи автора «Юров Виктор Михайлович»