Введение. Глобализация мировой экономики является одной из основных черт современного времени. Развитие международной торговли является существенной составляющей этого процесса на протяжении последних лет. Интеграционные экономические отношения влияют на характер международной торговли, принимает глобальные и региональные черты. Исследование моделей международной торговли, описывающие региональные и транснациональные отношения и смогут помочь контролировать и прогнозировать во времени взаимодействие между торговыми партнерами, безусловно актуальны.
В последние годы в исследованиях ученых рассмотрены глобальные и региональные направления экономической интеграции, в мировой экономике вызваны, с одной стороны, активной деятельностью транснациональных компаний (ТНК), а с другой – экономическим сближением государств в территориально-пространственном аспекте. Регионализация меняет конфигурацию составляющих экономики, вследствие чего мировое хозяйство становится уже не просто совокупностью всех стран мира, а определяется как единая система в которой взаимодействуют национальные и региональные секторы. Определяется триада международных регионов: европейский, североамериканский и азиатско-тихоокеанский. Отмечается, что торговля внутри региона превалирует [1,2]. В работах [3,4] определяется, что главной силой рыночного производства и международного разделения труда выступают ТНК, доля которых составляет 2/3 всей мировой торговли, 2/3 объема экспорта и такая же часть импорта приходится на развитые страны, а 1/3 – на развивающиеся страны и страны переходной экономикой. Развивающиеся страны, играют заметную роль в мировой торговле благодаря росту их экспортного капитала. Анализ количественных показателей международных торговых отношений, состояние России в этом процессе проведения в работах [5-8]. Подчеркнута необходимость развития экономического и торгового взаимодействия России как со странами запада, так и востока, особенно со странами-соседями.
Однако, в проведенных исследованиях мало обращались к экономико-математическим моделям международной торговли. В [9] рекомендуется использование и развитие международных логистических систем в обеспечении всех аспектов управления системой материальных потоков. Вероятностный подход к линейной модели международной торговли был предложен в [10-13], но динамика торгового процесса исследовалась только численными методами.
Постановка задачи. В связи с необходимостью развития и совершенствования экономико-математических моделей целью данной работы является получение в аналитической форме решений для линейной модели международной торговли за счет использования z-преобразований к аппарату цепей Маркова, который позволит определять пошаговое распределение общего бюджета между торговыми партнерами и скорость сближения процесса к стационарному состоянию.
Методология. Рассмотрим торговлю между ![]() странами с торговыми бюджетами
странами с торговыми бюджетами ![]() , которые используются на закупку товаров как на внутреннем рынке, так и в других
, которые используются на закупку товаров как на внутреннем рынке, так и в других ![]() стран.
стран.
Пусть ![]() - часть бюджета
- часть бюджета ![]()
![]() - й страны, используемая для закупки товаров
- й страны, используемая для закупки товаров ![]() -й страны, при этом
-й страны, при этом
.gif) , , |
(1)
|
Для любой ![]() -й страны общая сумма полученных денег равна
-й страны общая сумма полученных денег равна
.gif) , , |
(2)
|
Выражение (2) является условием сбалансированной бездефицитной торговли, модель которой представлена во многих учебниках, например, в [14].
Систему уравнений (2) можно представить в матричном виде:
|
|
(3)
|
из которого следует, что вектор-столбец ![]() является собственным вектором структурной матрицы
является собственным вектором структурной матрицы ![]()
![]() с собственным значением
с собственным значением ![]() . Таким образом, при заданной матрицы перехода между состояниями
. Таким образом, при заданной матрицы перехода между состояниями ![]() можно найти распределение бюджетов стран после значительного количества шагов-переходов между состояниями этой торговой системы.
можно найти распределение бюджетов стран после значительного количества шагов-переходов между состояниями этой торговой системы.
Применение теории цепей Маркова дает возможность получения динамических характеристик системы на пути к состоянию, когда распределение бюджетов между странами не меняется при дальнейшем развитии торгового процесса.
Рассмотрим матрицу ![]()
![]() , для которой выполняется условие (1):
, для которой выполняется условие (1):
.gif) |
(4)
|
Для транспонированной матрицы ![]() ее элементы удовлетворяют условиям:
ее элементы удовлетворяют условиям:
.gif) , , |
(5)
|
соответствующие определению элементов стохастической матрицы. Поэтому матрица ![]() определяет матрицу перехода (за один шаг) из состояния
определяет матрицу перехода (за один шаг) из состояния ![]() в состояние
в состояние ![]() цепи Маркова [15-17]. Таким образом, элементы
цепи Маркова [15-17]. Таким образом, элементы ![]() можно рассматривать как условные вероятности переходов из состояния
можно рассматривать как условные вероятности переходов из состояния ![]() в состояние
в состояние
.gif)
Для полного определения цепей Маркова еще необходимо задать начальное распределение ![]() :
:
.gif) |
(6)
|
Цепь Маркова называется эргодической, если с каждого состояния можно попасть в любой другой состояние.
Регулярной называется цепь Маркова, если какая-либо степень матрицы вероятностного перехода не имеет нулевых элементов, то есть в некоторый момент времени можно оказаться в любом из состояний этой цепи независимо от начального состояния процесса. Регулярная цепь Маркова всегда эргодическая.
Для цепей Маркова можно найти вероятность перехода из состояния ![]() в состояние
в состояние ![]() за
за ![]() шагов
шагов ![]() . Эта вероятность определяется величиной
. Эта вероятность определяется величиной ![]() , где
, где ![]() является элементом матрицы
является элементом матрицы ![]() , которая равна произведению
, которая равна произведению ![]() матриц
матриц ![]() , при этом вероятностный вектор
, при этом вероятностный вектор ![]() (распределение бюджетов стран через
(распределение бюджетов стран через ![]() шаг) является решением уравнения:
шаг) является решением уравнения:
|
|
(7)
|
Матрица ![]() регулярной цепи Маркова сходится
регулярной цепи Маркова сходится ![]() к некоторой матрицы
к некоторой матрицы ![]() , то есть ее элементы стремятся к соответствующим элементам матрицы
, то есть ее элементы стремятся к соответствующим элементам матрицы ![]() . Строки матрицы
. Строки матрицы ![]() создают одинаковый вероятностный вектор
создают одинаковый вероятностный вектор ![]() , все составляющие которого положительные. Этот вектор является единственным вектором, который удовлетворяет уравнению:
, все составляющие которого положительные. Этот вектор является единственным вектором, который удовлетворяет уравнению:
|
|
(8)
|
Система (8) является однородной и дает решение с точностью до константы. эта неопределенность ликвидируется за счет нормирования: .gif)
Таким образом, для больших значений ![]() долгосрочный прогноз распределения бюджетов стран (вероятностный вектор
долгосрочный прогноз распределения бюджетов стран (вероятностный вектор ![]() ) может быть определенным и неизменны. При этом он не зависит от начального распределения бюджетов.
) может быть определенным и неизменны. При этом он не зависит от начального распределения бюджетов.
Для изучения поведения цепи Маркова до перехода в предельное состояние воспользуемся z- преобразованием [18].
Пусть последовательность ![]() , которая не растет с ростом
, которая не растет с ростом ![]() быстрее геометрическая прогрессия, тогда
быстрее геометрическая прогрессия, тогда ![]() - преобразования
- преобразования ![]() последовательности
последовательности ![]() определим следующим образом:
определим следующим образом:
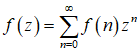
То есть, ![]() и ее преобразования
и ее преобразования ![]() связаны между собой взаимно-однозначное соответствие.
связаны между собой взаимно-однозначное соответствие.
Например, найдем z- преобразования для следующих последовательностей:
.gif)
.gif)
.gif)
![]()

.gif)
![]()
![]()
![]()
![]()
![]()
Заметим, что если последовательность ![]() с преобразованием
с преобразованием ![]() сдвигается вправо на единицу, то
сдвигается вправо на единицу, то
.gif)
Используем ![]() - преобразования уравнению (7) положив
- преобразования уравнению (7) положив ![]() :
:![]()
После преобразований получим
|
|
(9)
|
где ![]() - единичная матрица.
- единичная матрица.
Пусть ![]() является обратное преобразование к матрице
является обратное преобразование к матрице ![]() , которая является обратной к матрице
, которая является обратной к матрице ![]() , тогда из уравнения (9) имеем аналитическое решение нашей задачи:
, тогда из уравнения (9) имеем аналитическое решение нашей задачи:
|
|
(10)
|
Результаты исследований. Рассмотрим предложенную методику на примере. Пусть мы имеем линейную модель международной торговли между тремя странами. Структурная матрица торговли ![]() которой имеет вид:
которой имеет вид:
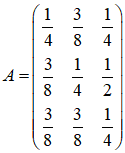
Транспонированная матрица ![]() является стохастической, а потому эту матрицу можно рассматривать как матрицу перехода цепи Маркова.
является стохастической, а потому эту матрицу можно рассматривать как матрицу перехода цепи Маркова.
Исследуем данную задачу с помощью![]() - преобразования. В нашем случае:
- преобразования. В нашем случае:
.gif)
так что 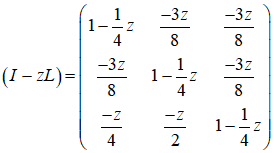 и
и
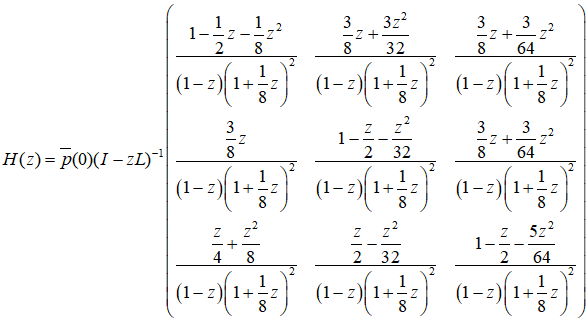
Каждый элемент матрицы ![]() представим в виде суммы двух слагаемых со знаменателями
представим в виде суммы двух слагаемых со знаменателями ![]() и
и .gif) :
:
.gif)
Поскольку ![]() является обратным преобразованием
является обратным преобразованием ![]() , тогда
, тогда
.gif)
где  ,
,
а .gif)
Относительно матриц ![]() и
и ![]() можно сделать где несколько замечаний.
можно сделать где несколько замечаний.
Замечание 1. Матрица ![]() для эргодического процесса всегда является стохастической матрицей финальных распределений цепи Маркова. Эту матрицу называют стационарной, так как она не зависит от
для эргодического процесса всегда является стохастической матрицей финальных распределений цепи Маркова. Эту матрицу называют стационарной, так как она не зависит от ![]() .
.
Замечание 2. Матрица ![]() совпадает с матрицей L (8).
совпадает с матрицей L (8).
Замечание 3. Для эргодического процесса матрица ![]() является бесконечно малой величиной с ростом
является бесконечно малой величиной с ростом ![]() . Эти матрицы интересны еще и тем, что сумма ее элементов по каждому ряду равна нулю. Матрицы с такими свойствами называют дифференциальными.
. Эти матрицы интересны еще и тем, что сумма ее элементов по каждому ряду равна нулю. Матрицы с такими свойствами называют дифференциальными.
Выводы. Таким образом предложенный метод z – преобразований позволяет благодаря установленной аналитический форме без использования компьютерной техники знать распределение общего бюджета между торговыми партнерами на каждом шагу эргодического цепи Маркова и определить время совпадения процесса к стационарному состоянию. Это позволит своевременно контролировать и корректировать процесс торговых отношений.
Библиографический список
- Садоян М. М. Национальная экономика в глобальном экономическом пространстве//Автореф. дисс. на соиск. уч. ст. канд. экономич. наук. М., 2008.
- Фролова Н.С. Современные тенденции развития международной торговли в условиях глобализации // Интернет-журнал «НАУКОВЕДЕНИЕ» Том 9, №3 (2017) http://naukovedenie.ru/PDF/108EVN317.pdf.
- Дюмулен, И.И. Международная торговля. Экономика, политика, практика: Монография / И.И. Дюмулен. – М.: ВАВТ, 2015. – 462 c..
- Аганбегян. Фундаментальный труд о мировом развитии. // Журнал МЭиМЭО. М., 2012. №2.
- Международные экономические отношения / Под ред. Е.Ф. Жукова. – М.: ЮНИТИ, 2011. – 860с.
- Амирова Д.Р., Гудкова В.С. Современные особенности внешнеэкономической деятельности Российской Федерации // Гуманитарные научные исследования. – 2014. – № 12
- Бойкова, И. П. Развитие трудового потенциала в условиях трансформации внешнеторговых отношений / И. П. Бойкова // Проблемы прогнозирования и государственного регулирования социально-экономического развития : материалы XVII Междунар. науч. конф., Минск, 20–21 окт. 2016 г. : в 2 т. / Науч.-исслед. экон. ин-т М-ва экономики Респ. Беларусь ; редкол.: А. В. Червяков [и др.]. — Минск, 2016 — Т. 2 — С. 103–104.
- Новиков В.В. Присоединение России к ВТО и ее участие в интеграции. Экономическая литература. – М.: Наука. МЭ и МО. 2011. -226 с.
- Гордей, К. Г. Логистические стратегии инновационного развития складской макроэкономической инфраструктуры: дис. … канд. экон. наук. – СПб., 2015. – 170 с.
- Г. Файоль, А. де Ля Фортель, “Энтропия и принцип больших уклонений для цепей Маркова с дискретным временем”, Пробл. передачи информ., 38:4 (2002), 121–135; Problems Inform. Transmission, 38:4 (2002), 354–367
- Довбенко М.В. Современные экономические теории в трудах нобелиантов: учебное пособие для студентов высших учебных заведений. / М. В. Довбенко, Ю.И. Осик. – М.: Акад. естествознания, 2011. – 305 с.: ил.: 20. ISBN 978-5-91327-155-6.
- Кундышева, Е.С. Экономико-математическое моделирование : учебник [Текст] / Е.С. Кундышева; под науч. ред. проф. Б.А. Суслакова. — М. : Дашков и К, 2008 — 424 с.
- Самаров К.Л., Шапкин А.С. Задачи с решениями по высшей математике и математическим методам в экономике: Учебное пособие – М.: Издательско-торговая корпорация «Дашков и Ко», 2007.
- Гармаш, А.Н. Экономико-математические методы и прикладные модели: Учебник для бакалавриата и магистратуры / А.Н. Гармаш, И.В. Орлова, В.В. Федосеев. – Люберцы: Юрайт, 2016. – 328 c..
- Большакова, Л.В. Теория вероятностей для экономистов: Учебное пособие / Л.В. Большакова. – М.: Финансы и статистика, 2009. – 208 c.
- Вентцель, Е.С. Теория случайных процессов и ее инженерные приложения / Е.С. Вентцель, Л.А. Овчаров. – М.: Высшая школа, 2007. – 479 c.
- А.Т. Баруча-Рид. Элементы теории Марковских процессов и их приложения. М.:Наука, 1969
- Ховард Р.А. Динамическое программирование и марковские процессы/ Р.А. Ховард. – М.: «Советское радио», 1964. – 195 с.
