АНАЛИЗ МОДЕЛИ ФИНАНСОВОГО ВЗАИМОДЕЙСТВИЯ ПРЕДПРИЯТИЙ В РЕГИОНАХ МЕТОДАМИ МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ

Постановка проблемы. Со времени принятия Бюджетного кодекса РФ в России проводится реформа межбюджетных отношений, в основу которой положен принципиально новую систему взаимоотношений между государством и регионами, имеет целью создание благоприятных условий для эффективного распределения бюджетных ресурсов в стране.
Основным направлением проведения реформы в России должно стать перераспределение финансовых ресурсов между бюджетом государства и соответствующего региона, урегулирования передачи бюджетных полномочий местным органам власти. В современных условиях государство должно обеспечивать эффективное перераспределение финансовых ресурсов между различными уровнями бюджетной системы, стабилизацию экономических и социальных процессов в обществе и тому подобное.
Рядом законодательных документов была утверждена стратегия регионального развития, в которой подчеркнуты необходимость оптимизации нормативно-правовой базы, которая предопределяет систему стратегических плановых и прогнозных документов, процедуры их разработки и реализации на всех уровнях территориальной организации власти и передача органам местного самоуправления полномочий и возложение ответственности за предоставление услуг населению.
Программа экономических реформ, предполагает перераспределение доходов между государственным и местными бюджетами.
Таким образом, моделирование товарно-денежной взаимодействия между структурными единицами регионов в условиях административно-территориальной реформы является актуальным.

Анализ последних исследований и публикаций. Денежные потоки между структурными единицами изучались многими учеными. В их исследованиях рассмотрены теоретические аспекты управления денежными потоками на предприятии, методы оптимизации денежных потоков организаций в процессе разработки бюджетов за счет ускорения привлечения денежных ресурсов, сдерживания выплат денежных ресурсов, т.е. внедрение действий на увеличение срока возврата средств и тому подобное. В ряде работ обсуждался метод уменьшения риска дефицита денежных ресурсов при использовании самострахования.
Ученые на основе вероятностного подхода обобщили исследования по управлению денежными потоками между организациями (региональными структурами) за счет введения дополнительного устойчивого вектора, который описывает действие власти для корректировки этого процесса. Во-первых, предложенная ими модель оказывается замкнутой, то есть сумма денег остается постоянной в системе, а действие власти только на каждом шаге процесса частично перераспределяет средства. Во-вторых, формула, которая описывает состояние системы на каждом шаге, имеет сложный вид и использует постоянный вектор корректировки финансовых ресурсов структурных единиц. Целью исследования является упрощение (при использовании метода z – преобразований) аналитического вида модели с управлением денежно-товарных потоков между структурными единицами выбранной системы, которая позволяет выравнивать финансовые ресурсы единиц в любом шаге за счет возможности определения вектора управления, а также выявление условий для открытости системы и текущих величин денежных потоков между выбранной и другими внешними системами.
Основные результаты исследования. Рассмотрим региональную систему, которая состоит из  структурных единиц, между которыми проходят финансовые операции (денежно-товарные потоки).
Пусть вектор  - начальное распределение финансовых ресурсов между структурными единицами, компоненты которого определяются государственными и региональными нормативными документами. Общий процесс товарно-денежного обмена между единицами через определенный промежуток времени (шаг) может быть представлен следующим модельным рекуррентным уравнением с матрицей L переходных вероятностей для эргодической цепей Маркова: 

(1)

- где  - вектор распределения финансовых ресурсов между единицами после  -того шага,  - вектор властного перераспределения (выравнивание) их ресурсов.
Матрица , которая определяется запланированными финансовыми действиями структурных единиц, имеет вид:

(2)

где  - величина финансовых ресурсов,  структурная единица передает  - той структурной единицы региона, а  - условная вероятность перехода системы из состояния и в состояние . Заметим, что модель (1) может быть применена для государственного регулирования финансовых ресурсов регионов.
Для аналитического изучения поведения цепей Маркова к переходу в стационарное состояние применяем метод  - преобразований в уравнение (1), при котором  переходит к  :

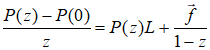(3)

После очевидных преобразований уравнение (3) принимает вид:

(4)

где - единичная матрица размером , а обратная матрца к матрицы 

Обозначим через  обратное преобразование матрицы  и представим эту матрицу в виде суммы слагаемых:

(5)

где  - стохастическая матрица, которая соответствует члену матрицы  со множителем .

Утверждение о стохастичности эквивалентно тому, что определитель матрицы  равен нулю при . Стохастичная матрица  всегда имеет хотя бы одно собственное значение, равное единице. Более того, строки матрицы  будут равны друг другу и составлять компоненты вектора предельных (стационарных) вероятностей состояния системы при . Матрицу  называют стационарной матрицей.
Составляющие матрицы , которые остались и обозначены через , определяют переходную ее составляющую, так как описывают поведение цепи Маркова в переходный период из состояния в состояние. Матрица в  интересна тем, что сумма элементов в каждой строке данной матрицы равна нулю. Такие матрицы получили название дифференциальных матриц.
Обратное преобразование в уравнении (4) определит выражение для вектора  состояния системы после  шагов, который включает через составляющие, пропорциональные , действие властных структур по перераспределению финансовых ресурсов между единицами и в котором произведение  определяет вектор стационарного состояния системы при . При запланированном состояния системы (вектор ), на который надо выйти через  шагов, уравнение  определит вектор перераспределения .
Получение выражения  при использовании  - преобразование позволяет аналитически анализировать и рассчитывать состояние системы на каждом шагу в отличие от выражения, приведенном в работе через произведение матриц .
Уравнение (1) описывает замкнутую систему взаимоотношений, так как при  денежно-товарное перераспределение между единицами проходит в рамках системы. Условие  необходимо для того, чтобы процесс перераспределения был сходящимся.
Проведенный анализ предложенной модели позволяет утверждать, что она не исключает взаимодействия структурных единиц за пределами замкнутой системы (определенных матрицы  и вектора )
Диагональные элементы матрицы  пропорциональны долям финансовых ресурсов, структурные единицы оставляют у себя при переходе из одного состояния в другое. Абсолютной величине этих ресурсов, которую можно планировать  -единицы для взаимодействия с внешними структурами, можно определить по формуле:

(6)

где  - -компонента вектора ,  - диагональные элементы стационарной матрицы , - -компонента вектора перераспределения. Если , то -единица взаимодействует только в замкнутой системе, а расчеты с партнерами проводит после продвижения к ней финансовых ресурсов из других единиц.
Рассмотрим на конкретном примере, как при помощи  - преобразования получить аналитический вид решении задачи управления финансовыми потоками между региональными структурными единицами.
Пусть стохастическая матрица , структура которой определяется запланированными бюджетами, описывает взаимодействие (потоки финансовых ресурсов) между структурными единицами региона и имеет вид:

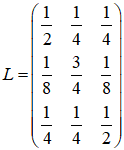(7)

Составим матрицу 

Найдем обратную матрицу к матрицы 

(8)

Полученное выражение подставляем в уравнение (4):

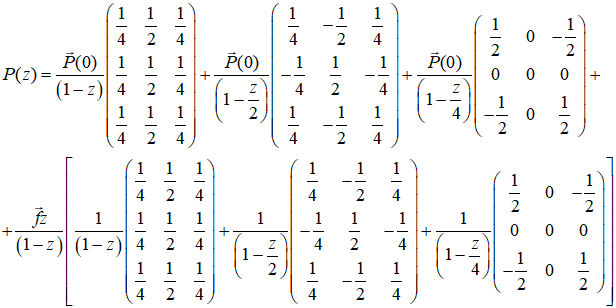(9)

Приводим все составляющие выражения (9) к виду, в котором они множителями простые дроби относительно , где  - постоянная величина:

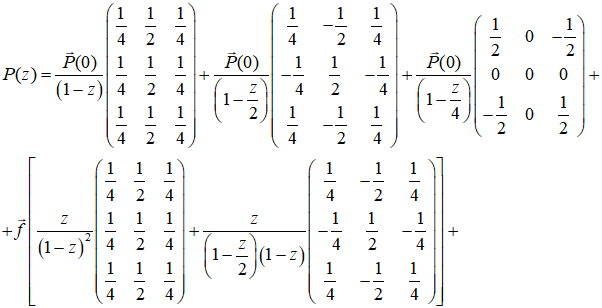	(10)
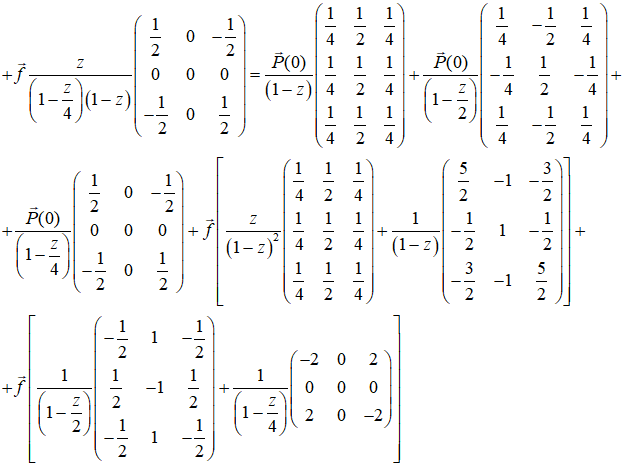	(10)

Выполним обратное преобразование в выражении (10)

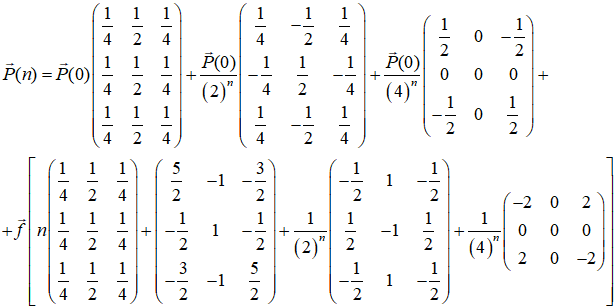(11)

Напомним, что для того, чтобы процесс распределения финансовых ресурсов между структурными единицами был сходящимся, необходимо и достаточно, чтобы сумма компонент вектора управления равна нулю:

(12)

При заданном векторе  формула (11) определяет вектор состояния системы после  шагов. При планировании граничного состояния системы в виде вектора  и заданного начального распределения необходимо приравнять его к вектору  при 

(13)

Из матричного уравнения (13), которое переходит в систему линейных уравнений и условия сходимости процесса (12), находим необходимое для этого значения вектора управления  :

(14)

Решение системы (14) имеет вид .
Материальные ресурсы, которые могут использовать структурные единицы для взаимодействия с внешними системами, равны  , , 
Значение  и  при планировании можно было бы увеличивать за счет  и , если бы перераспределение проходил в фиксированное время перехода системы из состояния в состояние.

Выводы. Анализируя вышеизложенное можно сделать следующие выводы: Усовершенствованная модель потоков материальных ресурсов в системе структурных единиц замкнутого пространства (регион, район и т.д.) благодаря использованию метода z – преобразований, который позволил упростить вид модели для проведения аналитического анализа и расчетов с большей точностью.
Проведенные исследования привели к определению путей взаимодействия структурных единиц с внешними системами и величин финансовых ресурсов, которые можно планировать для обмена на каждом шаге процесса.

1. Федеральный закон от 08.05.2010 № 83-ФЗ «О внесении изменений в отдельные законодательные акты Российской Федерации в связи с совершенствованием правового положения государственных (муниципальных) учреждений»;.
2. О Стратегии национальной безопасности Российской Федерации: Указ Президента Российской Федерации от 31.12.2015 г. № 683 // Собрание законодательства Российской Федерации (СЗРФ). 2015. № 1. Ч. 2. Ст. 212.
3. Прогноз социально-экономического развития Российской Федерации на 2012 год и плановый период 2013-2014 годов (разработан Минэкономразвития РФ)
4. Бланк И. А. Финансовый менеджмент: учебник / И. А. Бланк. – М.: Ника-центр, Эльга, 2002. -512 с.
5. Финансовый менеджмент. Управление денежным оборотом предприятия / под ред. Л.Н. Павловой. М.: Банки и биржи; ЮНИТИ, 2003.
6. Бочаров В. В. Управление денежным оборотом предприятий и корпораций / В. В. Бочаров. – М.:Финансы и статистика, 2002. – 144 с.
7. Барченко Н.Н. Управление денежными потоками промышленного предприятия: автореф. дис. … канд. экон. наук. СПб., 2000
8. Покровский Ю. Н. Методика анализа чистого денежного потока в условиях дефицита денежных средств / А. С. Кокин, Н. Ю. Покровский // Аудит и финансовый анализ. – 2010. – № 3. – С. 144-148.
9. Афанасьева Т.А. Проблемы и тенденции денежного обращения в России. URL: http://sisupr.mrsu.ru/2012-1/PDF/8_kds/Afanasyeva_Evstifeikina.pdf.
10. Тимофеева Т. В. Анализ денежных потоков предприятия / Т. В. Тимофеева. – М.: Финансы и Статистика; Инфра-М, 2010. – 368 с.
11. Балабанов И.Т. Финансовый менеджмент. М.: Финансы и статистика, 2008.
12. Витлинський В. В. Риск в менеджменте / В. Витлинський, С. И. Наконечный. – М.: Борисфен, 1996. – 330 с.
13. Корнейчук Н. Т. Риск и надежность. Экономико-стохастические методы и алгоритмы построения и оптимизации систем: монография / М. Т. Корнийчук, И. К. Совтус. – М.: КНЭУ, 2000. – 212 с.
14. Жлуктенко В. И. Стохастические процессы и модели в экономике, социологии, экологии: учеб. пособие / В. И. Жлуктенко, С. И. Наконечный, С. С. Савина – М.: КНЭУ, 2002. – 226 с.
15. Ховард Р. А. Динамическое программирование и марковские процессы / Г. А. Ховард. – М.: Советское радио, 1964. – 195 с.

Все статьи автора «Бадекин Максим Юрьевич»