Введение
Имеющаяся в нашем распоряжении информация об объектах микромира ограничена. Это затрудняет создание единой непротиворечивой теории и вынуждает использовать различные модели для объяснения различных явлений и свойств объектов. Академик Л.Д. Фадеев считал, что: «Основные законы квантовой механики не удаётся сформулировать как логическое следствие результатов некоторой совокупности фундаментальных физических экспериментов. Иными словами, до сих пор неизвестна формулировка квантовой механики, основанная на системе проверенных на опыте аксиом. Более того, некоторые из основных положений квантовой механики не допускают опытной проверки. Наша уверенность в справедливости квантовой механики основана на том, что все физические результаты теории согласуются с экспериментом. Таким образом, на опыте проверяются только следствия из основных положений квантовой механики, а не её основные законы» [1].
Рассмотрим простейшую ситуацию: основное состояние атома гелия (1s2) и его первое возбуждённое состояние (1s2s, 2 3S1). Разница энергий этих состояний составляет 159856 см-1 (0,7284 Ha (Eh)) [2]. Энергия ионизации атома гелия равна 2372,3 кДж/моль (0,9036 Ha), энергия ионизации иона He+ – 5250,4 кДж/моль (1,9998 Ha) [3]. Энергия ионизации гелия в состоянии 1s2s оценивается величиной 0,1752 Ha [4]. Отсюда следует, что энергия 1s-электрона в этом состоянии равна -1,9998 Ha. Если исходить из того, что каждый из электронов в 1s2 состоянии имеет равную энергию – по -1,4517 Ha, то получается, что процесс перехода атома гелия из возбуждённого состояния 1s2s в основное (1s2) доложен сопровождаться не только излучением с длиной волны 62,56 нм, но и поглощением излучения с длиной волны 83,04 нм, что необходимо для увеличения энергии 1s-электрона. Аналогично, процесс возбуждения атома гелия должен сопровождаться интенсивным излучением с длиной волны 83,04 нм, вызванным уменьшением энергии остающегося 1s-электрона. В противном случае, должен существовать некий безъизлучательный процесс перераспределения энергии между электронами.
Но есть и третий вариант, который состоит в том, что электроны в основном состоянии атома гелия имеют различную энергию: -0,9036 и -1,9998 Ha соответственно. Целью данной работы является проверка предложенной в [5] модели атома гелия, имеющего орбиты с различной энергией, путём расчета его спектра. Разработанная модель основана на постулатах Н. Бора и использовании модифицированного уравнения электростатического взаимодействия.
Модель атома гелия
Предложенная в 1913 г. Н. Бором планетарная модель атома включает три постулата [6]:
Электроны движутся вокруг ядра по круговым орбитам, так что сила электростатического притяжения FE равна центробежной силе:
где m, u и r – соответственно масса электрона, его орбитальная скорость и радиус орбиты.
Электрон в атоме может занимать ряд стационарных орбит (В действительности стационарной является только орбита с n = 1. Другие орбиты следует называть квазистационарными, поскольку время пребывания электрона на них очень мало), отличающихся величиной углового момента (angular moment). Причём величина углового момента электрона пропорциональна постоянной Планка h:
Частота излучения νba, при переходе электрона с орбиты номер b на орбиту номер a определяется разницей в энергиях данных орбит:
Этот подход позволяет с высокой точностью рассчитать спектр атома водорода и одноэлектронных ионов. Но в случае атома гелия Бор столкнулся с двумя проблемами.
Первая проблема состояла в том, как разместить два электрона относительно ядра. Бор, исходя из того, что оба электрона имеют одинаковое значение углового момента, поместил их на одной орбите, проигнорировав отталкивание между электронами.
Вторая проблема состояла в расчёте силы электростатического притяжения к ядру. Бор предложил собственное уравнение для взаимодействия между ядром с зарядом N и n электронами, находящимися на одной орбите:
.gif) , где е – заряд электрона. (4)
, где е – заряд электрона. (4)Вычисленная при этом энергия ионизации атома гелия оказалась равной 0,994 Ha, что всего на 10% больше экспериментальной величины [7].
Между тем известно, что круговая орбита обладает некоторыми гироскопическими свойствами, и мы вправе предположить, что отталкивание между электронами может привести к смещению плоскостей их орбит относительно ядра. На этой основе и с использованием модифицированного уравнения электростатического взаимодействия была разработана модель атома гелия и изоэлектронных ионов, в которой электроны движутся по равновеликим орбитам [8]. Ошибка в вычислении суммарной энергии электронов составила от -1% отн. для гидрид-иона до +1.5% отн. для иона О+6. Но, как было указано во введении, мы вынуждены отказаться от идеи равновеликих орбит и искать решение для системы с электронами, имеющими различную энергию.
Схема, описывающая данную систему, представлена на рис. 1. Модификация уравнения электростатического притяжения состоит в том, что к уравнению Кулона, описывающему взаимодействие электрона с ядром, добавляется поправка, учитывающая взаимодействие между электронами:
.gif) , (5)
, (5).gif) . (6)
. (6) 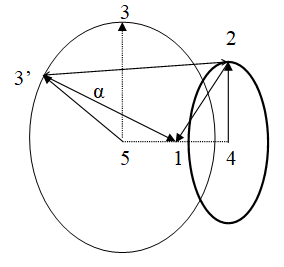
В модели принято равномерное распределение заряда по окружности орбиты в соответствии с концепцией А. Комптона о кольцевом электроне [9], так что элемент заряда:
Взаимодействие между элементами заряда на орбитах рассчитывается с использованием интеграла:
.gif) . (8)
. (8)При этом cosβ(α) и r(α)23 рассматриваются как функции от α. Int1(2,3) отличается от Int2(2,3) алгоритмом вычисления угла β. В первом случае это угол между r21 и r23, а во втором – между r31 и r32.
Силы электростатического притяжения электронов к ядру F21 и F31 имеют две проекции: на плоскость орбиты и на ось, на которой находятся центры орбит и ядро.
Проекция силы притяжения на плоскость орбиты уравновешивается центробежной силой:
.gif) , где ε1 – угол между r21 и r24. (9)
, где ε1 – угол между r21 и r24. (9)Выразив величину скорости движения из уравнения (2) и приняв во внимание, что радиус орбиты электрона в атоме водорода равен:
получим следующий эквивалент уравнения (1) [8]:
.gif) . (11)
. (11)В расчётах при подборе величины радиуса орбиты электрона r24 (соответственно r35), удовлетворяющего условию квантования (11), используется функция φ1 (φ2):
Проекции сил электростатического притяжения на ось, соединяющую центры орбит электронов, направлены в сторону ядра. Было найдено, что равновесие в системе можно описать следующим образом:
Полная энергия электрона складывается из потенциальной и кинетической энергии. Потенциальная энергия по определению есть величина отрицательная и равна произведению силы на расстояние. Кинетическая энергия электрона в модели Бора равна по модулю половине от его потенциальной энергии. Таким образом, энергии электронов равны:
Реализация модели сводится к тому, что бы найти значения r24, r14, r35 и r15 удовлетворяющие следующим условиям:
выполнение условия горизонтального равновесия по уравнению (13),
выполнение условия вертикального равновесия по уравнению (11) для каждого из электронов,
соответствие энергии каждого из электронов экспериментальной величине.
В возбуждённом состоянии структура атома может быть как аналогичной описанной выше, т.е. с орбитами электронов, сдвинутыми относительно ядра, так и с орбитами, лежащими в одной плоскости, включающей ядро (см. рис. 2). В последнем случае вид поправки к уравнению электростатического притяжения меняется:
.gif) , (15)
, (15)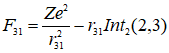 . (16)
. (16)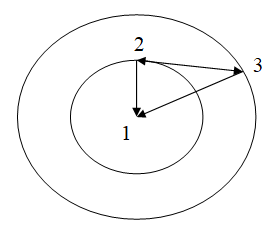
Наконец, возможен промежуточный вариант, когда плоскость одной орбиты (меньшего радиуса) проходит через ядро, а плоскость второй (большего радиуса) – сдвинута. В этом случае сила электростатического притяжения нижнего электрона (F21) вычисляется по уравнению (15), а верхнего электрона (F31) – по уравнению (6). Горизонтальное равновесие определяется по уравнению (13).
Для описания электронных состояний в статье используются следующие обозначения. Орбиты, лежащие в плоскости ядра, обозначаются как s, орбиты, сдвинутые относительно ядра – как p. Если две p-орбиты имеют одинаковый номер, то им присваивается дополнительный индекс. Таким образом, основное состояние атома гелия обозначено как 1p11p2.
Магнитные взаимодействия в модели не учитываются.
Результаты расчётов и обсуждение
В расчётах были использованы атомные единицы [10]: m = 9,1094·10-28 г, e = 4,8018·10-10 ![]() , с = 2,9979•1010 см/с, h = 6,6261 ·10-27 эрг·с, радиуса – равного радиусу орбиты электрона в атоме водорода (a0 = 5,2918·10-9 см), силы – равной силе электростатического притяжения, действующий на электрон в атоме водорода (F0 = 8,2339·10-3 дин), энергии – равной потенциальной энергии электрона в атоме водорода (1 Ha = 4,3597·10-11 эрг). Расчёты выполнены с шагом интегрирования π/1800. Точность вычисления энергии электронов – 0,0001 Ha.
, с = 2,9979•1010 см/с, h = 6,6261 ·10-27 эрг·с, радиуса – равного радиусу орбиты электрона в атоме водорода (a0 = 5,2918·10-9 см), силы – равной силе электростатического притяжения, действующий на электрон в атоме водорода (F0 = 8,2339·10-3 дин), энергии – равной потенциальной энергии электрона в атоме водорода (1 Ha = 4,3597·10-11 эрг). Расчёты выполнены с шагом интегрирования π/1800. Точность вычисления энергии электронов – 0,0001 Ha.
Структура, найденная для основного состояния атома гелия и соответствующая по энергетическим параметрам литературным данным (см. табл. 1, строка 1), не соответствует условию горизонтального равновесия. Результирующая сила притяжения между электронами составляет около 0,01 F0. Стабилизация структуры ведёт к уменьшению расстояния между электронами с уменьшением энергии системы. Действительно, величина энергии ионизации иона He+, равная 1,9998 Ha [3], превышает величину боровской энергии электрона (-2,0000 Ha). В атоме гелия энергия нижнего электрона должна быть ещё меньше за счёт воздействия верхнего электрона. Величина энергии нижнего электрона, найденная для относительно стабильной структуры (ΔFHor = 0,0003 F0), дающей совпадение с энергией ионизации атома гелия, составила 2,0006 Ha.
|
r24
|
r14
|
r35
|
r15
|
φ1
|
φ2
|
ΔFHor
|
E1
|
E2
|
|
1p11p2
|
||||||||
|
0,5000
|
0,0285
|
0,7438
|
0,2118
|
-6·10-5
|
2·10-4
|
1·10-2
|
-1,9998
|
-0,9036
|
|
0,4999
|
0,0279
|
0,7439
|
0,2112
|
2·10-5
|
-4·10-5
|
3·10-4
|
-2,0006
|
-0,9036
|
|
0,4999
|
0,0279
|
0,7439
|
0,2114
|
2·10-5
|
2·10-4
|
-9·10-6
|
-2,0006
|
-0,9033
|
|
0,5000
|
0,0271
|
0,7467
|
0,2139
|
-7·10-5
|
7·10-4
|
7·10-4
|
-2,0005
|
-0,8974
|
|
0,4999
|
0,0259
|
0,7503
|
0,2184
|
-3·10-6
|
-5·10-5
|
4·10-4
|
-2,0008
|
-0,8881
|
|
1p2p
|
||||||||
|
0,5000
|
0,0001
|
2,0003
|
0,0005
|
-4·10-7
|
-3·10-5
|
2·10-3
|
-2,0000
|
-0,4999
|
|
1p3p
|
||||||||
|
0,5000
|
0,0001
|
4,0005
|
0,0010
|
4·10-8
|
3·10-5
|
2·10-3
|
-2,0000
|
-0,2222
|
|
0,5000
|
0,0001
|
4,5164
|
0,0313
|
4·10-8
|
-8·10-5
|
2·10-3
|
-2,0000
|
-0,2206
|
|
1p4p
|
||||||||
|
0,5000
|
0,0001
|
8,0143
|
0,0280
|
6·10-8
|
-9·10-5
|
2·10-3
|
-2,0000
|
-0,1246
|
|
0,5000
|
0,0001
|
8,0989
|
0,1840
|
6·10-8
|
-9·10-5
|
2·10-3
|
-2,0000
|
-0,1220
|
|
1p7p
|
||||||||
|
0,5000
|
0,0001
|
24,5000
|
0,0001
|
6·10-8
|
1·10-4
|
2·10-3
|
-2,0000
|
-0,0408
|
|
0,5000
|
0,0001
|
24,6025
|
0,2000
|
6·10-8
|
-2·10-5
|
2·10-3
|
-2,0000
|
-0,0405
|
|
1p17p
|
||||||||
|
0,5000
|
0,0001
|
144,600
|
0,2000
|
6·10-8
|
-4·10-6
|
2·10-3
|
-2,0000
|
-0,0069
|
|
2p12p2
|
||||||||
|
1,8625
|
0,1020
|
2,2865
|
0,0800
|
-3·10-4
|
-9·10-4
|
7·10-4
|
-0,5766
|
-0,3826
|
|
1,8787
|
0,0921
|
2,3159
|
0,0898
|
9·10-5
|
-2·10-5
|
-1·10-4
|
-0,5666
|
-0,3729
|
|
1,8821
|
0,0882
|
2,3201
|
0,0902
|
-2·10-5
|
-1·10-4
|
-9·10-4
|
-0,5646
|
-0,3716
|
|
2p3p
|
||||||||
|
2,0000
|
0,0010
|
4,5034
|
0,0048
|
-6·10-5
|
5·10-4
|
3·10-4
|
-0,5000
|
-0,2219
|
|
2,0000
|
0,0010
|
4,5364
|
0,0462
|
-6·10-5
|
-3·10-4
|
1·10-3
|
-0,5000
|
-0,2187
|
|
2,0000
|
0,0010
|
4,5892
|
0,1120
|
5·10-5
|
5·10-5
|
2·10-3
|
-0,5000
|
-0,2137
|
|
2p10p
|
||||||||
|
2,0000
|
0,0030
|
50,0020
|
0,0040
|
1·10-5
|
1·10-5
|
8·10-4
|
-0,5000
|
-0,0200
|
|
2,0000
|
0,0030
|
50,1015
|
0,2000
|
-1·10-5
|
1·10-5
|
8·10-4
|
-0,5000
|
-0,0199
|
|
3p13p2
|
||||||||
|
4,4725
|
0,0116
|
5,3730
|
0,1720
|
-2·10-4
|
-1·10-5
|
-1·10-4
|
-0,2250
|
-0,1559
|
В табл. 2 приведены результаты расчётов для возбуждённых состояний типа 1sNs. Переходы из данных возбуждённых состояний в основное состояние приведены в табл. 3.
|
Состояние
|
r21
|
r31
|
E1
|
E2
|
|
1s2s
|
0,4998
|
4,1230
|
-2,0010
|
-0,1177
|
|
1s3s
|
0,4998
|
9,0537
|
-2,0008
|
-0,0549
|
|
1s4s
|
0,4998
|
16,0285
|
-2,0008
|
-0,0311
|
|
1s5s
|
0,4998
|
25,0150
|
-2,0008
|
-0,0200
|
|
1s6s
|
0,4998
|
36,0070
|
-2,0008
|
-0,0139
|
|
1s7s
|
0,4998
|
49,0010
|
-2,0008
|
-0,0102
|
|
1s8s
|
0,4998
|
63,9862
|
-2,0008
|
-0,0078
|
|
1s9s
|
0,4998
|
80,9910
|
-2,0008
|
-0,0062
|
|
1s10s
|
0,4998
|
99,9862
|
-2,0008
|
-0,0050
|
|
1s11s
|
0,4998
|
120,9814
|
-2,0008
|
0,0041
|
|
1s12s
|
0,4998
|
143,9764
|
-2,0008
|
0,0035
|
|
1s13s
|
0,4998
|
168,9710
|
-2,0008
|
0,0030
|
|
1s14s
|
0,4998
|
195,9655
|
-2,0008
|
0,0026
|
|
1s15s
|
0,4998
|
224,9597
|
-2,0008
|
0,0022
|
|
λ, нм [11]
|
ΔE, Ha
|
Переход
|
λ, нм
|
ΔE, Ha
|
Переход
|
|
50,55
|
0,9021
|
1s15s→1p11p2
|
50,86
|
0,8965
|
1s8s→1p11p2 |
|
50,57
|
0,9017
|
1s14s→1p11p2
|
51,00
|
0,8941
|
1s7s→1p11p2 |
|
50,59
|
0,9013
|
1s13s→1p11p2
|
51,21
|
0,8904
|
1s6s→1p11p2 |
|
50,62
|
0,9008
|
1s12s→1p11p2
|
51,56
|
0,8844
|
1s5s→1p11p2 |
|
50,66
|
0,9001
|
1s11s→1p11p2
|
52,22
|
0,8732
|
1s4s→1p11p2 |
|
50,71
|
0,8993
|
1s10s→1p11p2
|
53,70
|
0,8491
|
1s3s→1p11p2 (2) |
|
50,77
|
0,8981
|
1s9s→1p11p2
|
58,43
|
0,7804
|
1s2s→1p11p2 (3) |
|
59,14
|
0,7710
|
1s2s→1p11p2 (4) |
Для переходов от 1s15s→1p11p2 до 1s4s→1p11p2 включительно получено точное (в рамках принятой в работе погрешности) совпадение расчётных и экспериментальных значений длин волн. Но для переходов 1s3s→1p11p2 и 1s2s→1p11p2 обнаружилось определённое расхождение. Оно может быть объяснено следующим образом.
Особенностью состояний типа MpNp является их множественность, связанная с различными соотношениями радиусов орбит и их положений относительно ядра. Среди них есть более и менее устойчивые, более и менее соответствующие условиям квантования радиуса орбиты. Тем не менее, отклонения от равновесия в тысячных долях навряд ли можно считать условием, препятствующим возникновению таких состояний. Их образование может быть связано с динамикой процессов электронных переходов, т.к. одновременно с изменением радиусов орбит электронов происходит и смещение плоскостей орбит.
В табл. 1 приведены вариаций состояния 1p11p2. Основное состояние (строка 2) возникает при переходах с орбит 15s÷4s. При переходе электрона с орбиты 3s возникает состояние с энергией на 0,0003 Ha выше. Переход электрона с орбиты 2s может приводить к возникновению двух вариаций состояния 1p11p2 с энергиями верхнего электрона -0,8974 и -0,8981 Нa соответственно. Дальнейшая стабилизация этих вариаций связана с тепловым излучением.
Время электронного перехода определяется частотой излучения – ![]() . За этот промежуток времени плоскости орбит могут не успеть сдвинуться в равновесное состояние. По завершении процесса изменения радиуса орбиты электрона перемещения плоскостей орбит оказываются невозможными из-за того, что это приведёт к нарушению условия квантования радиуса (см. уравнение (11)). Так что на первой стадии возбуждения следует ожидать образования неравновесных вариаций состояний типа NpMp (преимущественно 1pMp). В табл. 1 приведены параметры некоторых из возможных структур этого типа.
. За этот промежуток времени плоскости орбит могут не успеть сдвинуться в равновесное состояние. По завершении процесса изменения радиуса орбиты электрона перемещения плоскостей орбит оказываются невозможными из-за того, что это приведёт к нарушению условия квантования радиуса (см. уравнение (11)). Так что на первой стадии возбуждения следует ожидать образования неравновесных вариаций состояний типа NpMp (преимущественно 1pMp). В табл. 1 приведены параметры некоторых из возможных структур этого типа.
Дезактивация состояний 1pMp может сопровождаться как образованием аналогичных структур, так и структур типа 1sMp. Вторичное возбуждение состояний 1sMp ведёт к образованию состояний 1sMs.
В спектре излучения гелия отсутствуют линии, соответствующие переходам 1sNs→1s2s, Это связано с тем, что при уменьшении радиуса орбиты внешнего электрона отталкивание между электронами ведёт к образованию состояний 1sMp и 1pMp, которые могут иметь близкие значения энергий электронов.
Возможность реализации различных видов переходов и наличие вариаций для одинаковых квантовых состояний обуславливает богатство спектра излучения атома гелия. В табл. 4 приведены переходы из состояний 1pNp. Как видно из таблицы они включают серии для нижних уровней 1s6p, 1s4p, 1p6p, 1p5p, 1p4p. Поскольку каждому из состояний соответствует множество вариаций, то переход из одного состояния в другое, гипотетически, может быть связан с несколькими линиями в спектре излучения. Например, переход 1p6p→1p5p может приводить к излучению в диапазоне от 1855 до 1954 nm. Это ведёт к тому, что по результатам расчёта энергии перехода сложно сделать отнесение конкретной линии к конкретному переходу. Например, линия при 1908,9 нм (0,0239 Ha) может быть вызвана переходами 1p6p→1s5p, 1p6p→1p5p, 1s6p→1p5p, 1s6p→1s5p, 1s8p→1p6p, 2p8p→2p6p, 2p6p→2p5p,. Использованная точность расчётов не позволяет осуществить выбор по длине волны излучения, но его, вероятно, можно будет сделать в дальнейшем на основе анализа геометрии состояний и динамики их образования.
|
Верхний уровень |
Нижний уровень |
|||||
|
Переходы 1pNp→1sMp |
||||||
|
1p17p |
1s4p |
|||||
|
1p16p |
1s8p |
1s6p |
1s4p |
|||
|
1p15p |
1s4p |
|||||
|
1p14p |
1s4p |
|||||
|
1p13p |
1s4p |
|||||
|
1p12p |
1s7p |
1s6p |
1s4p |
|||
|
1p11p |
1s7p |
|||||
|
1p10p |
1s6p |
1s4p |
||||
|
1p9p |
Переходы не идентифицированы | |||||
|
1p8p |
1s6p |
1s5p |
1s4p |
|||
|
1p7p |
Переходы не идентифицированы | |||||
|
1p6p |
1s5p |
1s4p |
1s3p |
|||
|
1p5p |
1s4p |
1s3p |
||||
|
1p4p |
1s3p |
|||||
|
1p3p |
Переходы не идентифицированы | |||||
|
1p2p |
Переходы не идентифицированы | |||||
|
Переходы 1pNp→1pMp |
||||||
|
1p17p |
1p4p |
|||||
|
1p16p |
1p8p |
1p6p |
1p4p |
|||
|
1p15p |
1p8p |
1p4p |
||||
|
1p14p |
1p6p |
1p4p |
||||
|
1p13p |
1p4p |
|||||
|
1p12p |
1p7p |
1p6p |
1p4p |
|||
|
1p11p |
1p5p |
|||||
|
1p10p |
1p8p |
1p6p |
1p4p |
|||
|
1p9p |
1p6p |
1p5p |
||||
|
1p8p |
1p6p |
1p5p |
1p4p |
|||
|
1p7p |
1p5p |
|||||
|
1p6p |
1p5p |
1p4p |
||||
|
1p5p |
1p4p |
1p3p |
||||
|
1p4p |
1p3p |
|||||
|
1p3p |
Переходы не идентифицированы | |||||
|
1p2p |
Переходы не идентифицированы | |||||
Анализ спектра даёт основания полагать, что при возбуждении атома гелия также образуются состояния типа 2pNp. Переходов, соответствующих дезактивации состояний типа 2sNs, 3sNs, 3pNp, выявлено не было.
Каталог NIST относит линию 32,03 нм (1,4226 Нa) к переходу 2p2→1s2p. В рамках данной модели мы имеем схожее отнесение перехода: 2p12p2→1p2p. Состояние 2p12p2 имеет множество вариаций с различными радиусами орбит электронов и их положением относительно ядра. В наибольшей степени рассматриваемому процессу подходит вариация (см. табл. 1), в которой электрон на нижней орбите 2p1 имеет энергию -0,5766 Ha, а на верхней орбите 2p2 – -0,3826 Ha. В состоянии 1p2p электрон на нижней орбите 1p имеет энергию -2,0000 Ha а на верхней орбите 2p – -0,4999 Ha. Следовательно, связанный переход должен сопровождаться двумя линиями излучения: при 32,01 нм (1,4234 Ha) и 388,70 нм (0.1172 Ha). Данный двулучевой переход иллюстрирует рис. 3. Мы получили расхождение с табличным значением для линии в ультрафиолетовой области в 0,02 нм (0,06% отн.) и в 0,16 нм (0,04% отн.) для линии в видимой области, которая относится к устойчивым [12].
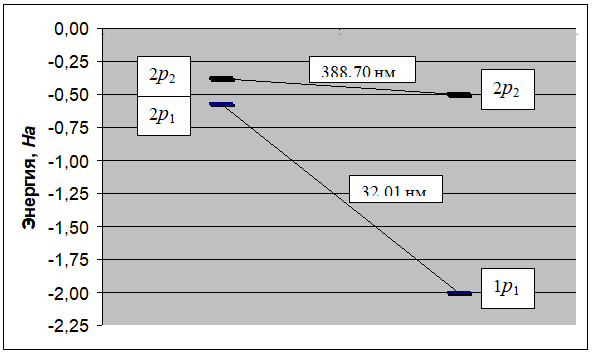
Аналогичные переходы, сопровождающиеся излучением двух фотонов, возможны ещё в нескольких случаях.
Линии при 294,5 нм (0,1547 Ha) и при 301,4 нм (0,1512 Ha) могут быть связаны с уменьшением энергии верхнего электрона (3p→2p2) при переходе 2p3p→2p12p2 для различных вариаций состояния 2p3p. При этом также уменьшается энергия нижнего электрона с -0,5000 до -0,5646 Ha. Линии соответствующие этому переходу присутствует в спектре (706,5 и 706,6 нм).
При возбуждении нижнего электрона из состояния 2p12p2 с образованием состояний 2pNp энергия верхнего электрона уменьшается до -0,5000 Нa. С этими процессами может быть связано образование линий 358,7 нм (0,1270 Ha), 361,3 нм (0,1261 Ha), 363,4 нм (0,1254 Ha), 370,5 нм (0,1230 Ha). Иного отнесения для перечисленных выше линий выявить не удалось.
Не удалось выявить и линий, соответствующих переходам 1p3p→1p2p, 1p3p→1p11p2, 1p2p→1p11p2. Дезактивация данных состояний может происходить через образование состояний 1sNs. Вероятно, наличие относительно устойчивых возбуждённых состояний обуславливает высокую светимость гелия, поскольку вторичное возбуждение требует меньших затрат энергии.
Заключение
Проведённое исследование показало, что модификация уравнения электростатического взаимодействия позволяет распространить теорию строения атома Н. Бора на двухэлектронные системы. Апробированная модель атома гелия, включающая лишь фундаментальные постоянные, позволяет без использования вариационных коэффициентов с высокой точностью рассчитать энергию электронов в основном и возбуждённых состояниях атома.
На основе проведённых расчётов удалось провести отнесение всех устойчивых линий в спектре атома гелия к переходам электронов между различными энергетическими уровнями исходы из положения о том, что образование излучения с конкретной частотой определяется изменением энергии конкретного электрона, а не всей системы в целом. Этот результат является важным для изучения механизмов генерации фотонов при электронных переходах и взаимодействия фотонов с электронами.
В тоже время, была выявлена множественность решения задач отнесения электронных переходов к линиям в спектре, что связано с вариативностью геометрической структуры определённых квантовых состояний и, как следствие, их энергетических характеристик. Дальнейшие исследования должны быть направлены на исследование динамики процессов возбуждения и дезактивации различных квантовых состояний атома и установлении правил отбора электронных переходов.
Библиографический список
- Фадеев Л.Д., Якубовский О.Я. Лекции по квантовой механике для студентов-математиков. – Ленинград: Издательство ЛГУ, 1980. – 200 с., с. 18.
- Energy Levels of Neutral Helium (He I). // Internet-site of The National Institute of Standards and Technology (USA). URL: https://physics.nist.gov/PhysRefData/Handbook/Tables/heliumtable5.htm (04.06.2018).
- Эмсли Дж. Элементы. – М.: Мир, 1993. – 256 с., с. 55.
- R. van Rooij, J.S. Borbely, J. Simonet, M.D. Hoogerland, K.S.E. Eikema, R.A. Rozendaal and W. Vassen. Frequency metrology in quantum degenerate helium: Direct measurement of the 2 3S1 → 2 1S0 transition. // ArXiv: 1105.4974v1 [physics.atom-ph], 25.05/2011. URL: https://arxiv.org/pdf/1105.4974.pdf (09.08.2019).
- Островский Н.В. Перспективы развития теории строения атома на основе постулатов Нильса Бора. // Проблемы исследования Вселенной, 2018, т. 38, вып. 2, с. 67-70.
- Bohr, N. On the constitution of atoms and molecules. // Philosophical Magazine, 1913, v. 26, p. 1-25.
- Bohr, N. Systems containing only a single nucleus. // Philosophical Magazine, 1913, v. 26, p. 476-502.
- Островский Н.В. Об энергии и структуре спаренных электронов. // Современная наука: актуальные проблемы теории и практики. Серия «Естественные и технические науки», 2013, № 1-2, с. 22-29.
- Томсон Г.П. Семидесятилетний // Успехи физических наук, 1968, т. 94, № 2, с. 361–370.
- Fundamental Physical Constants. Complete Listing 2018 CODATA adjustment. // Internet-site of The National Institute of Standards and Technology (USA). URL: https://physics.nist.gov/cuu/Constants/Table/allascii.txt (07.08.2019).
- Strong Lines of Helium (He) //Internet-site of The National Institute of Standards and Technology (USA). URL: https://physics.nist.gov/PhysRefData/Handbook/Tables/heliumtable2.htm (20.08.2013).
- Persistent Lines of Neutral Helium (He I). // Internet-site of The National Institute of Standards and Technology (USA). URL: https://physics.nist.gov/PhysRefData/Handbook/Tables/heliumtable3.htm (04.06.2018).
