Обзор решений парадокса близнецов в СТО
Парадокс близнецов берёт своё начало в основополагающей работе Эйнштейна “К электродинамике движущихся тел” от 1905 года. Это первый и наиболее известный парадокс СТО, сформулированный Эйнштейном как “своеобразное следствие” из факта замедления темпа хода движущихся часов. Статус “парадокса” и название “парадокс близнецов” появились позднее в результате расширения формулировки: согласно принципу относительности с точки зрения движущихся часов отставать должны неподвижные.
Более чем за сто лет после публикации работы Эйнштейна решению парадокса было посвящено множество статей, однако дискуссии по нему не прекращаются и в наши дни (2019 год). Видимо, главной причиной продолжающихся споров является то, что ни одно из предложенных решений, по сути, не является бесспорным. Аргументы, использованные разными авторами, нередко не дополняют, а противоречат друг другу, приводя к весьма спорным решениям парадокса. Практически всегда указывается, что парадокс близнецов в специальной теории относительности, её средствами не имеет решения, что для его решения необходимо использовать формализм общей теории относительности:
“При изучении СТО указывается, что “парадокс близнецов” не может быть объяснен в рамках этой теории. … Только в рамках ОТО мы можем понять и объяснить “парадокс близнецов” естественным образом, опираясь на положения OТО” [11, c.220].
“… парадокс близнецов … ограничен специальной теорией относительности, которую можно сразу отбросить из-за абсолютного характера ускоренного движения в этой теории” [3].
Согласно ещё одному замечанию [10, с.40], мнение о возможности использования формулы Лоренца для замедления времени в ускоренных системах ошибочно, поскольку эта формула “… справедлива только для инерциалышх систем и совершенно неприменима к системе R, скорость которой изменяется от v до – v.”Найти вместо этого уравнения “… уравнение, справедливое для системы R, в рамках специальной теории относительности невозможно, так как последняя справедлива лишь для систем отсчета, движущихся с постоянной скоростью” [10, с.40].
“Эйнштейн допускает существование парадокса, если он признает, что одной специальной теории относительности достаточно для анализа ситуаций, в которых нет истинного гравитационного поля” [5, с.2011].
“… парадокс часов есть результат ошибочного применения специальной теории относительности, именно ее применения к случаю, когда следует использовать общую теорию” [7 с.346].
Следует явно отметить, что у парадокса близнецов есть весьма широко используемая собственная проблема. Считается, что для сравнивания возрастов путешествующий близнец должен обязательно вернуться к своему брату. Однако это очевидная ошибка. Для того чтобы сравнить часы C с часами A, совсем не обязательно к ним приближаться. Вполне достаточно сравнить показания часов C с показаниями других часов B, которые синхронизированы с часами A, но могут находиться от них на любом расстоянии. То же самое относится и к парадоксу близнецов. Чтобы сравнить их возраст после того, как один из них удалился на большое расстояние, вполне достаточно сравнить возраст путешественника с возрастом ровесника своего брата в конечной точке путешествия. Или же просто посмотреть в этой точке на календарь, синхронный со всеми календарями в этой ИСО, относительно которой совершено путешествие. Более того, совершенно оставлено без внимания обстоятельство, что с определённой точки зрения, в противоположность традиционным решениям парадокса, путешественник окажется старше своего брата, остававшегося неподвижным.
Рассмотрим несколько вариантов решения парадокса (перевод статей наш). Выбор статей для рассмотрения произведён буквально наугад, но при условии наличия в них хоть какого-то решения, а не распространённого простого описания парадокса.
1. Еще одна заметка о парадоксе близнецов, Eisenlohr H.
В этой короткой заметке [2] автор использует вместо часов сердцебиения участников эксперимента, приняв их в состоянии покоя равными единице. Один из участников, астронавт удаляется от Земли со скоростью β на расстояние L, где мгновенно разворачивается и движется к Земле. На Земле, после возвращения астронавта мы просматриваем журналы двух участников и обнаруживаем в них следующие записи. В журнале астронавта указано, что за время полёта, равное T’, им отправлено на Землю R’emitted = 1×T’ = T’ импульсов его сердца. При этом им было получено с Земли, от второго участника количество импульсов его сердца, равное R’. В период удаления от Земли, равный T’/2, для астронавта частота сердцебиений землянина была пониженной:
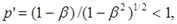
а на обратном пути – повышенной:
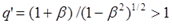
Следовательно, за весь период путешествия астронавт получил с Земли количество импульсов:
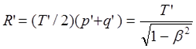 (7.1)
(7.1)
Не откладывая на потом, заметим, что пояснений к уравнениям для p’ и q’ автор заметки не приводит. Однако по виду уравнений догадываемся, что используются уравнения для релятивистского эффекта Доплера:
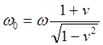
где принято, что скорость света равна единице, v – относительная скорость приёмника и источника. Если источник и приемник сближаются, то скорость имеет знак “плюс”. Если удаляются друг от друга, то скорость имеет знак “минус”. Таким образом, на этом этапе выкладки вполне корректны.
Далее в журнале земного близнеца находим схожие записи: количество отправленных астронавту импульсов равно Remitted = 1×T = T. С точки зрения землянина, частота поступающих импульсов от астронавта также меняется согласно эффекту Доплера. При удалении астронавта частота импульсов понижена:
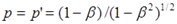
а на обратном пути – повышена:
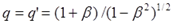
Но вот что интересно. “Половина” пути для земного близнеца в заметке оказывается смещённой. Импульсы повышенной частоты начинают поступать на Землю не ровно через половину времени в пути, а на величину времени, необходимого на приход сигнала из самой дальней точки траектории:
“Импульс, испускаемый в точке поворота, требует времени τ=L/c=(T/2)β, чтобы пройти расстояние L и достичь Земли”.
То есть, импульсы пониженной частоты приходят на Землю более длительное время, чем импульсы повышенной частоты. Исходя из этого, суммарное количество импульсов, полученных землянином равно:
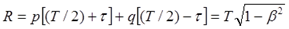 (7.2)
(7.2)
Теперь из простого сравнения полученных величин, находим, что землянин испустил T импульсов, а получил R импульсов, а астронавт, соответственно, испустил T’ импульсов, а получил R’ импульсов. Из чего делается вывод:
“Следовательно, оба близнеца приходят к одному и тому же выводу: во время путешествия сердце космонавта билось меньше в (1-β2)1/2 раза, чем сердце его брата. Кстати, формула для замедления времени получается, если положить R = T’ или R’ = T…”
Действительно, на первый взгляд всё строго сходится:
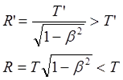
Однако обратим внимание на последнюю фразу в цитате “если положить…“. Воспользуемся указанным предположением, но в инверсном виде. Подставим в уравнение одно из этих соотношений:
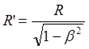
Сразу же возникает вопрос, в чём смысл этого нового, явно странного равенства? Обратимся к значениям этих же величин, полученных ранее, рассматривая их не как время, а как количества импульсов. Астронавт, как указано, испустил T’ импульсов, следовательно, землянин все их должен был получить. То есть, согласно сравнению величин, мы должны сделать несколько изменённую запись. Согласно исходным условиям задачи астронавт отправил на Землю R’ = 1×T’ = T’ импульсов своего сердца. Именно их и получил землянин, то есть, согласно уравнению (7.1):
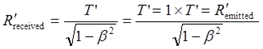
Здесь к величинам, обозначающим количества импульсов, мы добавили нижние индексы, поясняющие направление передачи, получателя и отправителя. Буквально полученное уравнение означает, что астронавт отправил на Землю R’ импульсов, а землянин получил R импульсов:
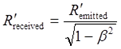 (7.3)
(7.3)
Ситуация противоречивая, невозможная: отправлено импульсов меньше, чем получено. Действительно, рассматривать ситуацию, когда получено импульсов больше, чем отправлено, не имеет никакого смысла. Как легко заметить, совпадут эти два количества только в единственном случае, когда астронавт никуда не улетал:
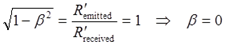
Обнаруженное противоречие не надуманное, а является следствием весьма завуалированной подмены понятий, которая произошла, очевидно, вследствие приравнивания частот сердцебиений единице. Проделаем повторно преобразования, отказавшись от этого приравнивания v0=v0‘ = 1. Тогда астронавт за время полёта, равное T’, отправил на Землю R’emitted = v0‘T’ импульсов своего сердца, где индекс emitted мы добавили выше как для уточнения отправителя, так и во избежание одинаковых обозначений, поскольку R’ обозначает количество импульсов, полученных землянином. Приняв v0‘ = 1, мы, разумеется, получим тот же результат, что и ранее. Но при отличии частот сердцебиений от единицы результат уже несколько иной. В период удаления от Земли, равный T’/2, для астронавта частота сердцебиений землянина была пониженной:
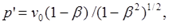
а на обратном пути – повышенной:
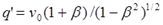
Следовательно, за весь период путешествия астронавт получил с Земли количество импульсов вместо (7.1):
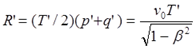 (7.4)
(7.4)
Соответственно, и для землянина при удалении астронавта частота импульсов понижена:
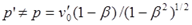
а на обратном пути – повышена:
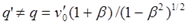
То есть, в общем случае частоты получаемых сигналов сердцебиений не равны для участников. С учётом времени получения последнего сигнала до разворота, суммарное количество импульсов, полученных землянином вместо (7.2) равно:
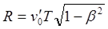 (7.5)
(7.5)
Вот теперь мы можем принять некоторые конкретные, условные значения величин и описать их физический смысл. Пусть v0 = v0‘ = v60 ≈ 60 ударов в минуту. Тогда уравнения (7.4) и (7.5) можно записать в расшифрованном виде. С Земли астронавт получил следующее количество импульсов:
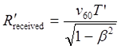 (7.6)
(7.6)
Соответственно, землянин получил от астронавта импульсы в количестве:
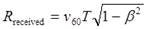 (7.7)
(7.7)
Обращаем внимание, что произведения v60T’ и v60T не просто количественно равны, соответственно, отправленным импульсам с Земли R’emitted = v60T’ и от астронавта Remitted = v60T, это и есть эти величины, которые ранее были обозначены как R’ и R. Отметим, что штрихи в уравнениях (7.6) и (7.7) и других вносят некоторую двусмысленность, которую мы снимаем окончательно нижними индексами, точно указывая получателя-отправителя:
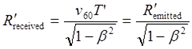
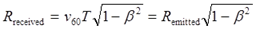
Мы пришли к выражениям, подобным выражению (7.3), и выявили источник подмены понятий. Рассматривать ситуацию, когда получено импульсов меньше, чем отправлено, не имеет никакого смысла. Таким образом, хотя метод решения парадокса, описанный в заметке, оригинален, но решить парадокс близнецов как таковой он не позволил.
2. Парадокс близнецов и принцип относительности, Grøn Ø.
Отметим, что традиционное замечание о возможности решения парадокса в специальной теории относительности приводится в самом начале, во введении к рассматриваемой статье:
“Можно сразу избавиться от парадокса близнецов, заметив, что для того, чтобы встретиться, отойти и встретиться снова, по крайней мере, один из близнецов должен ускориться. А в рамках специальной теории относительности принцип относительности не действует для ускоренного движения. Ускорение абсолютно. Следовательно, по крайней мере, один из близнецов не может считать себя в состоянии покоя. Близнец с наибольшей средней скоростью между событиями P1 и P2 будет моложе, когда близнецы встречаются в P2″ [3, с.1].
Однако далее автор всё-таки использует парадокс близнецов, как он указал, в качестве “педагогического входа в общую теорию относительности”. При этом он ссылается на Эйнштейна, который указал на необходимость расширения постулата относительности на любые виды движения, а не только инерциальные. Исходя из этого, теперь уже “оба близнеца имеют право считать себя в состоянии покоя”. В качестве примера автор рассматривает обычную версию парадокса с полётом близнеца к ближайшей звезде Альфа-Проксима. Звезда находится в 4-х световых годах от Земли. Скорость полёта туда и обратно равна v = 0.8c. Автор вычисляет с точки зрения Земли возраст близнеца A, остававшегося на Земле, и возраст близнеца-путешественника B в момент его возвращения, которые равны:
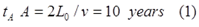
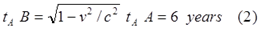
Затем, используя принцип относительности, он делает такие же расчёты, считая теперь находящимся в покое близнеца B, а движущимся – близнеца A. Поскольку теперь движущимися являются Земля и звезда, то этот интервал близнецу B виден сократившимся [3, с.3]:
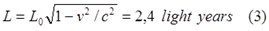
Следовательно, с его точки зрения он провёл в пути [3, с.4]:
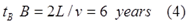
Таким образом, предсказания обоих близнецов относительно возраста близнеца B совпали:
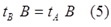
Но вот в отношении возраста близнеца A их предсказания разнятся. По мнению близнеца B его брат состарится меньше [3, с.4]:
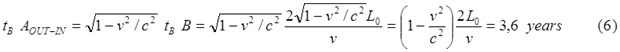
Однако это вычисление вызывает некоторое недоумение. Автор выше отметил, что близнец B “видит” трассу Земля-звезда укороченной, поскольку эта трасса является движущимся стержнем в его системе отсчёта. Следовательно, близнецу B определённо известно, что в собственной системе покоя её длина больше, чем вычисленная по уравнению (3):
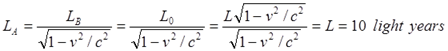
Поэтому близнец B должен определить время старения A как время, за которое он, близнец B с точки зрения A совершит своё путешествие:
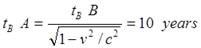
В этом случае предсказания двух близнецов совпали бы и в отношении старения близнеца A, что означает строго корректное решение парадокса близнецов в рамках специальной теории относительности. На этом дальнейшие выкладки мы могли бы опустить, поскольку нас как раз и интересовал способ решения парадокса в рамках СТО. Однако это решение автор отклонил, обосновав это в выводах тем, что в рассмотренной ситуации:
“… ускоренный близнец не имеет права говорить, что он находится в покое, потому что гравитационное поле, которое он испытывает, не имеет источника. Это специальное гравитационное поле вводится в описание, когда мы говорим, что близнец A находится в покое, а B путешествует” [3, c.12].
Это довольно странно, поскольку выше он указал, что трасса Земля-Звезда близнецу B видна сократившейся, а это является прямым следствием преобразований Лоренца, если считать близнеца B неподвижным. Тем не менее, вывод сделан и он совпадает с традиционным мнением, что СТО неприменима из ускоренных систем отсчёта, поэтому в ней парадокс не имеет решения и даже не может быть корректно сформулирован. Дальнейшие выкладки автор приводит уже без использования формализма специальной теории относительности.
3. Парадокс близнецов и принцип Маха, Lichtenegger H. and Iorio L.
Авторы статьи рассматривают различные варианты парадокса близнецов. Но мы обратимся только к разделу работы, рассматривающему парадокс в формулировке, близкой к традиционной. В этом варианте близнец-путешественник не возвращается в исходную точку, а сравнение его возраста в конечной точке пути производится с возрастом третьего участника в неподвижной системе отсчёта. Такой вариант правильнее назвать парадоксом трёх часов или парадоксом ровесников. Сами авторы назвали этот вариант “модифицированной версией стандартного парадокса близнецов“.
Основным достоинством этого варианта является то, что в процессе движения не используются ускорения, и применение формализма общей теории относительности здесь не требуется. Вариант не имеет принципиальных отличий от традиционного, поскольку возрасты двух близнецов или показания часов рядом с ними, находящихся в неподвижной системе отсчёта всегда тождественны. Поэтому сравнивать возраст путешественника можно с любыми часами в этой неподвижной системе отсчёта.
В работе учитываются текущие показания часов, то есть, в начальный момент движения они не обнулены. Следствием этого стали довольно длинные уравнения и замысловатые обозначения переменных, изобилующие “крышками” – короткой горизонтальной чертой над переменной, эквивалентами обычных штрихов. Рассматривая выкладки, мы сделаем два изменения: вместо “крышек” будем ставить традиционный штрих – неподвижные участники A и B, а путешественник – A’. Показания всех часов в начальный момент движения примем равными нулю. Уравнения станут заметно короче, но, хотя это будут, по сути, другие уравнения, мы будем давать им прежние, авторские номера.
Итак, в работе рассмотрены два состояния участников: в начальный момент времени и после перемещения в неподвижной системе K. Скорость перемещения путешествующих часов A’ и их наблюдателя в конечную точку равна V. Расстояние перемещения из положения A в положение B равно Δx = AB. В конечной точке наблюдатель A’, находящийся в движущейся ИСО K’, встречается с третьим участником B. По часам неподвижных наблюдателей A и B от начала движения и до этой встречи прошёл интервал времени [4, с.3]:

Наблюдатель A’ движется инерциально относительно K, поэтому с точки зрения этой ИСО и наблюдателей A и B часы A’ покажут время:
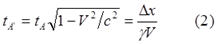
Следовательно, разница в показаниях часов B и A’ при их встрече в ИСО K равна:
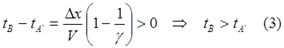
С другой стороны, с точки зрения часов A’ и наблюдателей в ИСО K’ движущейся является ИСО K и находящиеся в ней часы A и B. Однако наблюдатели в K’ видят, что интервал Δx испытал лоренцево сокращение, стал короче, поскольку движется со скоростью V относительно ИСО K’. Следовательно, с точки зрения A’ и K’ время в пути составило:
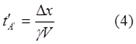
Здесь мы должны заметить, что в отличие от парадокса с ускоренным движением при развороте, в данном случае наблюдатель в движущейся ИСО K’ имеет полное право считать себя неподвижным. В этом случае для наблюдателя A’ часы, находящиеся в ИСО K теперь уже не синхронизированы, с его точки зрения, вследствие движения, они показывают разное время. В соответствии с преобразованиями Лоренца он считает, что часы B опережают часы A с коэффициентом ΔxV/c2, причём, как мы установили для начального момента, t’A = 0, т.е.:
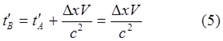
Действительно, уравнение преобразований Лоренца для времени имеет вид:
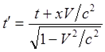
Правое слагаемое в числителе и есть это опережение (5) двух движущихся часов, разделённых интервалом x. По той же причине движения часов A и B относительно ИСО K’, интервал времени движения, отображаемый часами B, с точки зрения K’ на этом интервале движения от A к B (4) сокращается, уменьшается относительно tA = tB с коэффициентом γ−1, то есть время t’B, увиденное в K’ на часах B при встрече с A’, равно сумме сократившегося интервала (4) и опережения (5) часов B над часами A:
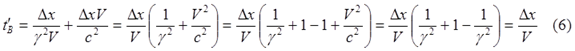
Таким образом, часы A’ с точки зрения ИСО K’ с показаниями (6) отстают от часов B с показаниями (4) на время:
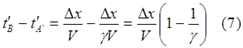
Часы A’ находятся в состоянии покоя в ИСО K’ и показывают меньший интервал времени между показаниями, полученными при последовательном, поочерёдном сравнении с парой часов A и B, синхронизированных в ИСО K. Таким образом, сравнение пар уравнений (2) с (4) и (1) с (6) показывает, что оба наблюдателя – A и B в ИСО K и наблюдатель A’ в ИСО K’ приходят к согласию о показаниях часов при одновременной проверке их в одном и том же месте. Иначе говоря, в рассмотренном варианте парадокса близнецов в формализме специальной теории относительности нет никакого парадокса и моложе при встрече оказался путешественник A’.
4. Парадокс близнецов, Witman D.M.
Рассматриваемый парадокс близнецов описан в одной из глав данного учебника, предлагаемого как курс теории относительности для неспециалистов. Парадокс рассматривается в традиционном виде, а в качестве близнецов выступают ставшие традиционными участниками в квантовой физике близнецы, ровесники Алиса и Боб. Алиса улетает на ракете в путешествие по галактике. В процессе путешествия близнецы ежегодно посылают друг другу радиосигналы с приглашениями на свои дни рождения.
В общем, представленная картина традиционна: по возвращению Алиса оказывается моложе Боба. При этом отмечено, что парадокс возникает, если применяются правила для инерциального движения к явно неинерциальному движению Алисы [6, с.117]. В этом отношении представляет особый интерес напоминание о том, что Алиса не может рассматривать движение Боба как ускоренное, поскольку у неё есть объективные тесты для определения собственного ускоренного движения. Из этого делается и традиционный вывод, что из-за релятивистского замедления времени в инерциальной системе отсчёта Боба действительно моложе именно Алиса.
Словесное решение парадокса сопровождается диаграммами Минковского и не содержит уравнений. Большое внимание уделено тому, что наблюдает путешествующая Алиса, что сопровождается множеством рисунков, правда, довольно абстрактных: круги – планеты и космолёты, на фоне которых изображены годы их текущего времени.
Следует с сожалением отметить, что такая художественная иллюстрация довольно слабо улучшила понимание, аргументацию. Например, планеты с одинаковыми датами на их фоне ничего, по существу, не добавили к тексту в подписи к рисунку 10.3:
“На мгновение остановившись на развороте, Алиса обнаруживает, что все часы планет снова синхронизированы по значению часов локальной планеты. Она прочитали на них четыре года с начала ее путешествия, несмотря на то, что прошло всего два года по ее собственным часов” [6, с.120].
Поясняется, что в этот момент Алиса ненадолго перешла в систему покоя планет. Это устранило релятивистское искажение времени, и Алиса оказалась в том же 2529 году, что и на этих планетах, несмотря на то, что была в пути только 2 года, начав его в 2025 году:
“Алиса уже моложе Боба, и обратный путь лишь увеличит эффект вдвое, повторяя процесс. Ключевым действием была смена системы отсчёта, также известная как ускорение. Ускорение фактически не повлияло ни на какие часы планеты, но оно изменило набор отдаленных событий, которые Алиса считает одновременными событию здесь и сейчас” [6, с.120].
Задаётся, можно сказать, риторический вопрос:
“Кажется, что-то волшебное произошло во время ускорений Алисы. Как, например, часы планет могли внезапно стать синхронизированными, когда она замедлилась при повороте?” [6, с.120].
Однако последующий ответ на него, рассуждения о перекосах сетки пространства-времени и о “перемотке времени” через часть жизни Боба, довольно туманны и плохо раскрывают суть возникших преобразований. Интересно замечание, что величина ускорения сама по себе не влияет на изменение возраста Алисы, не вызывает замедления её старения по сравнению с Бобом. На этом, собственно, конструктивное описание парадокса завершено. В качестве корректного научного решения парадокса близнецов принять его сложно.
5. Новый взгляд на парадокс близнецов, Бузмаков И.В.
Данную работу мы рассматриваем критически, несмотря на то, что в интернете, на форуме она была подвергнута весьма серьёзной, даже разгромной критике. Мы не будем сравнивать, совпала наша критика с критикой на форуме или нет, а просто укажем на некоторые ошибки в этой работе. Как заявил автор:
“Доказана невозможность объяснения парадокса в рамках теории относительности при движении одного из близнецов по такой траектории” [8].
Доказательство представлено с помощью схемы движения рис.1 в статье:

Рис.1. Разворот часов U2 в точке B по окружности.
Рассмотрены двое часов U1, находящиеся в неподвижной системе отсчёта K в точке A, и часы U2, в системе отсчёта K‘, движущиеся по замкнутой траектории, состоящей из двух прямолинейных, инерциальных участков, и участка разворота по дуге окружности радиуса r.
Отметим, что схема содержит неинерциальный отрезок пути, поэтому в доказательстве рассматривается эффект падения часов U1 в эквивалентном гравитационном поле. При этом утверждается, что в отличие от известных доказательств используются не приближенные, а точные формулы теории относительности, что, по мнению автора, позволило получить такие же абсолютно точные соотношения.
Тем не менее, некоторые допущения всё-таки довольно условны. Заявлено, что при развороте часы U2 не тормозят, а продолжают лететь с той же скоростью V, но по дуге радиуса r вокруг точки B, что, как считается, вроде бы исключает скачкообразное изменение направления скорости часов U2 в точках начала и конца разворота. Однако такой разворот с изменением скорости на противоположную назвать плавным можно весьма условно, поскольку радиус дуги довольно мал. Тем не менее, это допущение можно принять как вполне безобидное. Но вот следующее рассуждение выглядит весьма двусмысленно:
“Так как наблюдаемое из К изменение показаний часов U2, произошедшее при их развороте, имеет некоторую конечную величину, и так как часы U2 при движении вдоль отрезка АВ идут медленнее часов U1, то при достаточно большой длине отрезка АВ часы U2 по возвращении в точку А должны отставать от часов U1 на некоторое время ∆t1” [8].
В действительности всё то же самое можно сказать и о наблюдениях из системы K‘, если учесть, что эта система отсчёта некоторое время является неинерциальной, и часы U1 с её точки зрения на этом этапе идут ускоренно, быстрее часов U2. В результате, согласно приведённой ссылке, отстающими оказываются часы U2 и парадокс снимается сразу же.
Далее мы изменим порядок рассмотрения ситуации с точек зрения каждой системы отсчёта. Сначала традиционно рассмотрим ситуацию, как она описана в статье, с точки зрения изначально неподвижной системы K.
“В системе отсчета K часы U2 все время двигаются со скоростью V. Учитывая, что согласно специальной теории относительности с точки зрения часов U1 часы U2 идут медленнее в γ раз …, получаем, что время ΔTU2, затраченное часами U2 на путешествие, должно быть равно:
ΔTU2 = ΔTA/γ (7)
Автор использует величину лоренц-фактора γ = (1 – V2/c2)–1/2 > 1. Однако, замечаем, ΔTU2 содержит также и неинерциальную составляющую – время разворота по часам U2. На этом интервале движения медленнее часы идут согласно общей теории относительности, поэтому лоренцев коэффициент в этом случае неприменим.
Теперь рассмотрим эту же картину с точки зрения движущейся системы отсчёта K‘ с часами U2. Автор указывает, что
“Учитывая, что согласно специальной теории относительности на участках равномерного и прямолинейного движения с точки зрения часов U2 движущиеся часы U1 идут медленнее в γ раз …, имеем:
∆τ′U2 = γ∙∆τ′A (3)
Здесь допущена распространённая ошибка. Дело в том, что в этом уравнении время ∆τ′A – это не суммарное время ∆τ′A, прошедшее по часам U1 на участках равномерного и прямолинейного движения, входящее в уравнение (2):
ΔT′A = ∆τ′A + ∆t′A (2)
Для их различения уравнение (3) следует записать иначе:
∆τ′U2 = γ∙∆τ′′A (3a)
Если же использовать авторское значение ∆τ′A, то уравнение (3) должно иметь инверснвый вид:
∆τ′U2 = ∆τ′A/γ (3б)
Связано это с тем, что длина отрезка AB имеет разную величину с точки зрения систем отсчёта K и K‘. Действительно, с точки зрения движущейся системы K‘ этот отрезок движется ей навстречу, поэтому испытывает лоренцево сокращение. Время на прохождение со скоростью V часами U2 этого интервала с точки зрения часов U1 равно:
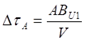
Соответственно, время на прохождение со скоростью V часами U1 этого интервала с точки зрения часов U2 равно:
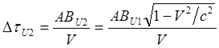
Сравнивая эти времена, находим
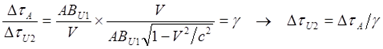
что отличается от уравнения (3) и совпадает с уравнением (3б). По этой же причине следует изменить и соотношение времени на разворот. Если использовать некорректное, лоренцево сокращение интервалов времени на неинерциальном участке и исправленное уравнение (3б), то в этом случае уравнение (5) примет следующий вид:
ΔT′U2 = ∆τ′A/γ + Δt′A/γ (5)
Воспользовавшись сформулированным в статье правом, приравниваем исправленное уравнение (5) и уравнение (8), получив в результате тождество:
∆τ′A/γ + Δt′A/γ = ∆τ′A/γ + ∆t′A/γ
Получается, что вывод автора о приходе к противоречию специальной теории относительности с ее основным постулатом ошибочен. Заявление автора о том, что все полученные им соотношения абсолютно точны, поскольку в представленных расчетах он не использовал никаких приближений, также неверно. Кроме того, рассуждения в статье содержат явную геометрическую ошибку:
“На участке разворота система К′ является вращающейся системой отсчета с центром в точке B, поэтому в ней существует гравитационное поле, в котором часы U2 неподвижны, а часы U1, вращаются с угловой скоростью ω вокруг неподвижной точки B, где находятся точно такие же часы UB” [8].
Это утверждение геометрически некорректно, ошибочно. Очевидно, что часы U1 не могут вращаться вокруг точки B по радиусу r, поскольку они попросту находятся дальше от этой точки. Можно было бы предположить, что по этому радиусу r вокруг часов U2 вращаются синхронные с U1 часы UB, находящиеся в центре вращения B. Однако и это неверно, что легко показать вычислениями. Движение часов U2 вокруг часов UB напоминает движение автомобиля по кольцу. Центр кольца всегда неподвижен относительно автомобиля. Таким же образом часы U2 всегда движутся “лицом вдоль траектории”, поэтому часы UB по отношению к ним на рисунке всегда слева. Следовательно, и падают в эквивалентном гравитационном поле вращающихся часов U2 именно неподвижные часы UB.
Таким образом, вывод о том, что рассмотренный мысленный эксперимент не может быть непротиворечиво описан в рамках теории относительности является ошибочным.
6. Парадокс часов, Мардер Л.
Парадокс в книге рассматривается в наиболее полном, сложном варианте, в котором движение путешественника разбивается на 5 этапов. Отмечается, что с точки зрения неподвижного, земного участника три участка ускоренного движения занимают непродолжительное время по сравнению с участками инерциального движения [9, с.83]. Считая, в общем, что продолжительность инерциального движения с обеих точек зрения существенно превышает продолжительность времени ускорения, разворота и торможения, которым можно пренебречь, делается очевидный вывод: время в пути по часам путешественника меньше времени по часам земного наблюдателя.
Пренебрегая временем неинерциального движения, мы приходим к традиционной формулировке парадокса близнецов. На участках инерциального движения теперь уже можно неподвижным рассматривать путешественника, вследствие чего, меньшее время должны показать часы на Земле.
Решение парадокса производится на диаграмме Минковского. Отмечается, что критерии одновременности на двух участках инерциального движения в системе отсчёта путешественника не одинаковы. Далее утверждается, что при наблюдении путешественником Земли не будет никаких разрывов, и земные часы не будут “идти в бешеном темпе”. Однако последующее пояснение имеет довольно туманный смысл:
“Быстрое изменение происходит лишь с критерием одновременности, но это не играет физической роли, так как понятие одновременности на расстоянии – дело условное. И все же это понятие прекрасно срабатывает, когда требуется рассчитать абсолютный результат вроде различия времени путешествия часов, сначала разлетающихся друг от друга, а затем вновь встречающихся. [9, с.86].
Далее приводятся достаточно детальные ссылки на взгляды разных авторов на парадокс. В заключение сторонникам мнения, что периоды ускоренного движения путешественника “могут быть последовательно рассмотрены лишь в общей теории относительности” [9, с.87] противопоставляется мнение, что “общая теория относительности мало что добавляет к истолкованию парадокса часов, если нет реальных гравитационных полей, хотя в фокусе всех споров находится именно такой случай” [9, с.202].
Собственно решение парадокса близнецов в рамках специальной теории относительности этим и ограничивается. Назвать его исчерпывающим и убедительным мы не можем.
7. Сказка о двух близнецах, Benguigui L.
В этой работе автор отмечает, что по парадоксу близнецов в специальной теории относительности: “Похоже, что во многих статьях есть ошибки” [1, с.3] и указывает, что он рассматривает, даёт общий обзор только тех решений, которые, как утверждается, находятся в рамках специальной теории относительности [1, с.25]. В частности автор схематично рассмотрел несколько вариантов применения преобразований Лоренца в контексте парадокса близнецов и получил специфические выводы. Поскольку обозначения переменных в цитатах общепринятые, их расшифровку мы не приводим. Рассматривая продолжительность некоторого процесса в двух относительно движущихся ИСО, автор приходит к классической, наивной формулировке парадокса близнецов:
“Можно считать, что τ – это истекшее время пути для каждого близнеца в его собственной системе (земле или ракете), и каждый из них измеряет время γτ для другого. Вопрос в том, какие времена измеряются в обеих системах, когда они снова встречаются?” [1, с.5].
Наивность заключается в том, что происходит отождествление времён, на самом деле качественно не связанных друг с другом, фактически это времена, относящиеся к двум парам разных событий. Правильнее говорить, что один близнец измеряет времена τ и γτ, а другой – t и γt. Именно такое отождествление и лежит в основе традиционной формулировки парадокса. Точно такое же отождествление автор производит и для расстояний:
“Третий случай интересен для расследования … Какова связь между двумя расстояниями L и L’? Поскольку существует полная симметрия между двумя точками зрения в S и в S’, времена, измеренные в S и S’, должны быть равны. Это приводит к тому, что L = L’ и, в частности, нет “сокращения длины” [1, с.6].
Здесь происходит отождествление теперь уже двух пар расстояний, обозначим их как L1 и L’1 и L2 и L’2. Каждая пара расстояний относится к одной из рассмотренных систем отсчёта и качественно они не эквивалентны, поскольку L1 и L2 – это собственные длины в своих ИСО, это два разных отрезка, два разных стержня. Возникает вопрос: это мнение автора или он приводит мнение других исследователей, с которым он не согласен? Пояснений в статье мы не увидели.
Далее в своём анализе автор демонстрирует возможность применения формализма СТО к ускоренно движущимся системам отсчёта. Для этого интервал движения такой системы разбивается на последовательность инерциальных систем отсчета, имеющих также название мгновенно сопутствующая инерциальная система отсчёта – МСИСО. Эти ИСО можно рассматривать как последовательные интервалы исходной неинерциальной системы отсчета. Для такой неинерциальной системы отсчёта собственное время определяется интегрированием коэффициента Лоренца с переменной скоростью:
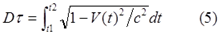
Это уравнение позволяет вычислить показания часов, движущихся с переменной скоростью, и показывает, что формализм СТО применим к ускоренно движущимся системам отсчёта с точки зрения обычной инерциальной системы. В качестве примера рассматриваются две ИСО S и S’, движущиеся навстречу, причём перед самой встречей ИСО S’ изменяет свою относительную скорость до нуля, то есть, останавливается в ИСО S. Эта ситуация описывается уравнением:
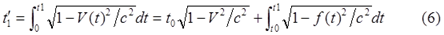
Принимается, что часы двух систем обнулены на момент начала движения. Интеграл после первого знака равенства – это общее время движения ИСО S’ с точки зрения неподвижной системы S. Первое слагаемое справа – время инерциального движения S’ с точки зрения S, второе слагаемое – время, в течение которого движущаяся система S’ замедлилась до остановки. Как утверждается, интеграл правой части (6) меньше, чем (t1 – t0), следовательно, t’1 < t1 и при их встрече часы S’ покажут меньшее время, чем часы S. При мгновенной остановке t0 = t1, и интеграл в правой части (6) обращается в ноль. Поэтому t’1 = t1/γ, что является традиционным решением парадокса при мгновенном развороте путешественника.
Описывается также и ещё один корректный вариант решения. Если дистанция между ИСО “привязана” к системе S’, то возникает противоположное решение парадокса: t’1 > t1. Иначе говоря, в этом случае путешественник оказывается старше близнеца, остававшегося неподвижным [1, с.7]. Также корректно рассмотрен последний вариант, когда обе ИСО движутся встречно с одинаковой скоростью относительно третьей, неподвижной системы отсчёта. В этом случае при встрече показания их часов будут тождественными. Отметим небольшую неточность в выкладках. При объяснении взглядов Ланжевена на парадокс близнецов автор приводит схему движения, рис.1 в статье, и поясняет:
“Штриховые линии BK и BL – это мировые линии световых сигналов, посылаемых путешественником. Сигнал BK – это последний сигнал, отправленный непосредственно перед его обратным ходом, а BL – первый сигнал, который он отправил сразу после начала своего обратного хода” [1, с.10].
Как видно на рисунке, при такой трактовке световой сигнал BK должен двигаться в прошлое. Далее делается традиционное замечание по парадоксу с ускорением:
“Поскольку система отсчета путешественника ускоряется относительно системы отсчета Земли, она не является инерциальной. Тем не менее, решение проблемы в ИСО Земли может быть достигнуто с помощью специальной теории относительности, но решение в ИСО путешественника с помощью общей теории относительности даст больше понимания” [1, с.12].
Другими словами, землянин может использовать формализм СТО, а путешественнику следует обратиться к ОТО. Рассмотрен также и вариант с тремя системами отсчёта, названный в статье решением без ускорения. От Земли близнец удаляется инерциально в одной системе, а в точке обычного разворота просто перескакивает в такую же ИСО, но движущуюся к Земле. При этом показания своих часов (возраст) он сохраняет неизменными. Этот вариант, следует заметить, отличается от своего традиционного аналога трёх ИСО, в котором никто не перескакивает, просто возвратно движущиеся часы устанавливаются в показания только что прибывших с Земли. При перескакивании близнец испытывает ускорение. Поэтому следует признать ошибочным утверждение автора статьи, что этот сценарий не использует ускорения, следовательно, совместим со специальной теорией относительности. Это неверно, поскольку ускорение просто завуалировано и соответствует мгновенному развороту.
Вместе с тем, следует признать ошибочным и другое утверждение, отрицающее указанное утверждение о совместимости в части величины ускорения. Это утверждение, высказанное при рассмотрении гравитационного решения Мёллера, что:
“… время в точке поворота, несмотря на то, что оно происходит на нулевом расстоянии, не равно нулю при измерении в системе отсчёта “остающегося дома”! Это приводит к тому, что общее время ΔT имеет разрыв в точке поворота. Это является причиной нарушения симметрии во временах двух близнецов. Меллер объясняет этот особенно удивительный результат тем, что в таком случае (g → ∞) гравитационный потенциал бесконечен. Этот результат очень важен, потому что он показывает, что, даже если времена ускорения очень короткие, существует асимметричное старение. Очень часто утверждается, что, если времена ускорения очень малы, ускорение становится несущественным для проблемы, и это неверно” [1, с.17].
Вывод о ненулевом времени получен в результате некорректных аналитических выкладок. Нулевое расстояние разворота ведёт к тождественно нулевому времени разворота. А при любом коэффициенте соотношения между временами в движущейся и покоящейся системах второе, относительное время также будет равно нулю. Это верно даже для поля гравитации Чёрной дыры: нулевые интервалы времени под горизонтом событий и над горизонтом – тождественны.
“… столь частый аргумент о том, что короткие времена ускорения делают их ненужными, является ложным. … полные расчеты показывают, что разница в возрасте обусловлена двумя факторами: ускорением и замедлением времени” [1, с.27].
При желании расчёты могут показать любой желаемый результат. Хорошо известны решения, использующие мгновенный разворот путешественника, с нулевым временем ускорения. Это, конечно же, приводит к невозможному, бесконечно большому ускорению, однако в этом гипотетическом случае парадокс решается строго в рамках специальной теории относительности и строго в соответствии с другими корректными решениями, с более молодым путешественником в конце полёта. Формально в этом случае путешественник всё время двигался инерциально, без ускорения. В этой связи следует отметить интересное замечание автора:
“В неускоренной версии близнецы никогда не находятся в одной и той же системе отсчета, и, таким образом, нет ни поездки одного из них, ни возвращения на Землю” [1, с.23].
Этот вывод, по меньшей мере, является неоправданным упрощением. Неускоренную версию можно назвать традиционной, “жёсткой” версией парадокса близнецов. Действительно, речь идёт о соотношении показаний двух относительно движущихся часов, роль которых нередко исполняют близнецы. Близнецы заметно усложняют задачу, поскольку для них в неускоренной версии общей точкой является только место их рождения. Но для часов это не проблема. В пределах бесконечно протяжённой неподвижной ИСО существует любое число синхронизированных часов. Следовательно, в варианте трёх ИСО из исходной точки могут начать путешествие часы, синхронизированные с неподвижными. А в точке условного разворота обратно могут двигаться такие же часы, синхронизированные с прибывшими в эту точки путешествующими часами. В исходной точке сравниваются неподвижные часы и эти, возвращающиеся. Никаких ускорений в этом случае не требуется и вариант формально полностью эквивалентен “жёсткому” варианту парадокса. Действительно, для того чтобы узнать время на другом конце страны, нам не обязательно ускоряться и ехать туда, поскольку все часы синхронизированы.
Рассмотренный обзор решений в статье приводит к выводу, что в классической, “жёсткой” формулировке парадокс не имеет не только решения средствами специальной тории относительности, но он даже не может быть в ней сформулирован просто по определению инерциальной системы отсчёта.
Вместе с тем, хотя и с некоторой долей неуверенности, в расширенных и, по сути, эквивалентных формулировках парадокс близнецов в специальной теории относительности имеет непротиворечивое, корректное решение. Все разногласия и разночтения относятся к разным вариантам его формулировки.
8. О решении Эйнштейна парадокса пары часов, Unnikrishnan C. S.
В данной работе автор критически анализирует решения Эйнштейна и делает вывод, что решение, использующее гравитационное замедление времени, “… страдает от логических и физических недостатков и дает неправильные ответы в общем контексте” [5, с.2009]. Буквально это можно трактовать, что решение парадокса близнецов не нуждается в использовании гравитационных полей. Анализ и выводы автор делает в отношении редко цитируемой работы Эйнштена:
“Поскольку сам документ не очень известен, и поскольку расчет не часто обсуждается в контексте парадокса близнецов, я восстанавливаю его здесь. Вывод здесь более подробный, чем приблизительный расчет, упомянутый в некоторых обсуждениях, и, возможно, более подробный, чем имел в виду Эйнштейн …” [5, с.2011].
В результате восстановления расчетов Эйнштейна, автор приходит к традиционному виду парадокса близнецов [5, с.2012], двум уравнениям, противоречию: близнец А стареет меньше, чем В и, наоборот, близнец B стареет меньше, чем A:
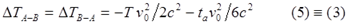
Заметим, что при выводе замедления с точки зрения движущегося близнеца ΔTA-B, автор использует некорректные предположения о равенстве ускорений при развороте с разных точек зрения. Однако ускорение само зависит от времени разворота с точки зрения каждого из близнецов. Получается, что во втором случае, с точки зрения движущегося близнеца B для вычисления времени замедления темпа хода часов A в уравнении требуется использовать (через вычисление ускорения) это самое искомое время. Далее, используя гравитационное замедление, автор приходит к следующему выводу [5, с.2012]:
“Общее замедление времени A относительно B равно
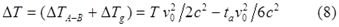 “
“
Однако выкладки выгдядят подозрительно. Проверим их. Для удобства записываем исходные уравнения, использованные в (8):
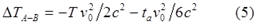
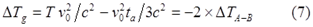
Подставляем их в первое равенство (8):
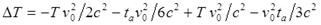
Собираем подобные члены:
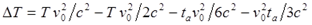
Подробные преобразования делаем, чтобы не упустить мелкие детали:
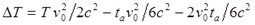
Окончательно получаем уравнение (8a) и добавляем для сравнение проверяемое уравнение (8):
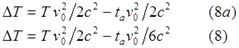
Это очень странно, но предложенное автором заключительное выражение не соответствует исходным данным, использованным при его выводе. Заодно замечаем, что и уравнение (7) явно не соответствует уравнению (5). Опечатка? Если учесть, что в статье неоднократно делается ссылка на логику, то это более чем странно.
Можно сказать, что в заключение в статье приведены два контрпримера, на основании которых делаются весьма далеко идущие выводы:
“… все стандартные решения парадокса-близнецов, использующие ускорение или эквивалентное псевдо гравитационное поле в качестве физического эффекта, ответственного за асимметричное замедление времени, ошибочны, и решение Эйнштейна не является исключением. Таким образом, решение Эйнштейна, использующее общую теорию относительности, принцип эквивалентности и гравитационное замедление времени, просто не работает, за исключением конкретного случая, состоящего только из двух часов в совершенно особой последовательности движения. Следовательно, это решение парадокса часов, равно как и любое, которое основано на каком-то физическом эффекте, связанном с ускорением, должно быть отвергнуто. … возможность выключения или остановки часов делает все стандартные решения неадекватными” [5, с.2014].
Надо отметить, что, в общем, мы разделяем позицию о чрезмерности формализма ОТО для решения парадокса близнецов. Для его решения вполне достаточно собственных средств специальной теории относительности. Однако со следующим фундаментальным заявлением, спорным заявлением автора согласиться можно лишь с большой долей осторожности:
“Утверждение … о том, что не существует физического метода измерения скорости движения в пространстве, аннулируется различными маркерами, доступными в космологии …” [5, с.2015].
В заключение отметим, что при наличии объёмной, но всё-таки определённо спорной аргументации, опровержений традиционных гравитационных решений, автор, тем не менее, не привёл хотя бы кратких аналитических доводов, уравнений в пользу решений без формализма ускорений и общей теории относительности.
Библиографический список
- Benguigui L., A tale of two twins, https://arxiv.org/abs/1212.4414
- Eisenlohr H., Another Note on the Twin Paradox, Amer. J. Phys., 36, 635 (1968)
- Grøn Ø., The twin paradox and the principle of relativity, https://arxiv.org/abs/1002.4154
- Lichtenegger H., Iorio L., The twin paradox and Mach’s principle, arXiv:0910.1929v2, 2011
- Unnikrishnan C. S., On Einstein’s resolution of the twin clock paradox. CURRENT SCIENCE, VOL. 89, NO. 12, 25 DECEMBER 2005
- Wittman D.M., The Elements of Relativity. Oxford University Press (2018)
- Борн М. Эйнштейновская теория относительности, перевод с английского Н.В. Мицкевича. – 2-е изд., испр. – М.: МИР, 1972
- Бузмаков И.В., Новый взгляд на парадокс близнецов, // Современные научные исследования и инновации. 2014. № 6. Ч.1 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2014/06/36247
- Мардер Л., “Парадокс часов”, Пер. с англ. А.А.Бейлинсона, с предисловием Н.В.Мицкевича, Изд. “МИР”, Москва, 1974.
- Мёллер К., Теория относительности, Изд. 2-е. Пер. с англ. Под ред. проф. Д. Иваненко. М.: Атомиздат, 1975, 400 с.
- Розман Г.А. Теория относительности. – Псков: ПГПУ, 2005. – 256 с.
- Путенихин П.В., Парадокс близнецов – обзор решений. Содержание, URL: http://samlib.ru/p/putenihin_p_w/twin00.shtml
