Introduction

The gravitational constant is among the fundamental physical constants associated with universal physical laws and theories. At the same time, a special feature of the gravitational constant is that its value does not follow from any mathematical relationship. That is why the accuracy feature was steadily the crucial point of each measuring of the gravitational constant [1]. The aim of this article is to show, that in regard to the accuracy achieved up-to-date, the row of values of the gravitational constant can be considered as measurement spread. This approach makes the accuracy in frames of
exponential representation of the gravitational constant considered not higher than two decimal places of the mantissa. In the fallowing we will proceed exactly from this hypothesis.

Brief history

The gravitational constant G first appeared in the law formulated by Newton in 1666 and therefore is also called Newtonian constant of gravitation. The first measurement of the gravitational constant was carried out in 1798 by Henry Cavendish (G = 6.754⋅10^-11). In its experiments the torsion balance appliance was used designed by geologist John Mitchell [2].

The complexity of the measurement of the gravitational constant bases on the fact that the force of gravity is too small to be measured with the guaranteed accuracy. Ат the same time the biggest problem is the influence of the earth’s gravity which must be eliminated when measuring. In turn, this induces the problem of the obtaining of exact value of the Earth density. Therefore, the further experiments have required more sophisticated equipment that appeared only much later.

Stochastic simulation

Lately, measurement of the gravitational constant were carried out repeatedly especially in the period of the last forty years. It seemed this made it possible to improve the accuracy of measurements, nevertheless it did not lead to the final result. Below, in the Tab. 1 the results of the measurement of the gravitational constant registered by CODATA (The Committee on Data for Science and Technology [3]) are given in the chronological order.

As these results have been obtained by different researcher teams we can assume that they are independent in statistical sense. Let us consider a hypothesis that the spread in the decimal places after the base value of 6.67 has a stochastic nature. In order to examine the spread of the measurement data, we have used the stochastic simulation approach [4]. The results of this simulation are also given in the Tab. 1.

Tab. 1 The measurement of the gravitational constant.

The data of the columns in the Tab. 1 are visualized in the Fig. 1.

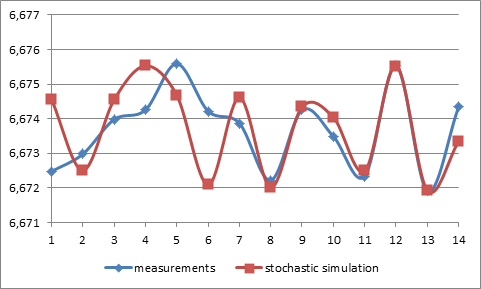
Fig. 1 The values of the gravitational constant vs. the stochastic simulation.

This chart is of interest in relation to the striking similarity of measurement data and the results of the simulation. The spread of the data in regard to the base value 6.67 is shown in the Tab. 2 and Tab. 3.

Tab. 2 The measurement data spread

Tab. 3 The stochastic simulation data spread

Now, should be the similarity of these two data series formally proved, we will have right to assume that the data spread after the second decimal place is similar to the uniform distribution.

Let choose the statistical measure of the similarity of the two sets in the form of correlation factor [5]:

        υ_x,y = Cov(X,Y)/(σ_x·σ_y)                            (1)

Then for the data in the Tab.1 (as a single simulation series) we obtain the well suited value υ_x,y ≈ 0.65. Anyway, by the multiserial simulation the average correlation factor is ῡ_x,y ≈ 0.25 that in view of the small size of the sets should be considered as a valid confirmation of our hypothesis formulated above [5].

Discussion

In regard to the Tab. 1 the gravitational constant can be also represented in the form:

G = 6.67·10^-11+ η                                 (2)

where: η < 10^-13 - the measurement spread.

Otherwise, the equality it can be rewritten in a more elegant way:

        G = σ·c^-1                                    (3)

where:

c – speed of the light in free space

0.0200129 ≤ σ ≤ 0.0222551

For example, by σ = 0.02 and c = 299.792.458 we obtain exactly:

        G = 6.671281903963·10^-11

On the other hand, the CODATA recommended value of gravitational constant is G = 6.67408⋅10⁻¹¹ [3]. In this case σ ≈ 0.0200084. In addition, the equality (3) can be used for obtaining a modified form of the Planck units [6].

Tab. 4 The modified form of the Planck units (ᵬ = (ℏ/σ)^1/2, ᵭ = (ℏ·σ)^1/2, k - the Boltzmann
constant).

The modified form of the Planck units in the Tab. 4 can be considered as more preferable because of it uses only the true universal constant which is the speed of light in free space [3].

In addition, the equality (3) leads to the fact that the gravitational constant loses its status of fundamental constant since it is expressed through the other fundamental constant i.e. the light speed in free space.

Conclusion

Above, the results of determination of the gravitational constant obtained over a long period are considered. By means of stochastic simulation it is shown that the spread of the gravitational constant data can be described with the uniform distribution. A formal statement for determination of gravitational constant and the associated modified representation of the Planck units are derived.

The author does not in any way suspect the results obtained earlier through complex and apparently expensive experiments. At the same time for such experiments in the future, it is worth to ask oneself about the really meaningful accuracy of the gravitational constant, which from our point of view is virtually limited to the second decimal place of the mantissa of exponential data record. However, the accuracy of the gravitational constant can undoubtedly be improved by increasing the accuracy of the tools used for its measurement.

1. Terry Quinn, Clive Speake. The Newtonian constant of gravitation – a constant too difficult to measure: Philos. Trans. A., Math Phys Eng Sci., 13, 2014.
2. Wolfgang Schreier (Hrsg.). Geschichte der Physik. GNT-Verlag GmbH, Berlin: 2002, 447 s.
3. Peter J. Mohr, David B. Newell, Barry N. Taylor. CODATA recommended values of the fundamental physical constants: Rev. Mod. Phys. 88, 2014.
4. Rubinstein Reuven Y., Kroese Dirk P. Simulation and the Monte Carlo Method. Wiley Series in Probability and Statistics: 2016, 432 p.
5. R.Cody, J.Smith. Applied statistics and the SAS programming Language. Pretence Hall: 1991, 600 p.
6. Wikipedia. Physical constant. URL: https://en.wikipedia.org/wiki/Physical_constant

Все статьи автора «Сучилин Владимир Александрович»