Introduction
In the paper [1], the use of the Lorentz transformation in the ordinary differential equations was considered which describe behavior and properties of time-dependent systems in inertial reference frames (IRF). The similar approach is possible with respect to the problems of mathematical physics, where, in addition to the time variable, spatial coordinates are used in which physical processes are taking place. As well-known, these processes are described by partial differential equations with initial and boundary conditions [2]. In the present paper, the substituting of Lorentz ratios (LR) in these equations is considered and the consequences resulting from this are discussed.
Lorentz transformations
The Lorentz transformations belong to the mathematical apparatus of the Special relativity and describe relationship between two IRF one of which is fixed and the other moves relative to the first with a constant speed. The core of these transformations is Lorentz factor (LF) [3]:
γ = ![]() (1)
(1)
where
v – the speed of the moving IRF
c – the speed of the light in vacuum.
In the following, two specific LR will be used:
1) In the time domain:
Δt´= γ·Δt (2)
where
Δt – the time interval in the fixed IRF
Δt´- the time interval in the moving IRF,
and
2) In the spatial domain:
Δr´= Δr / γ (3)
where
Δr – the length interval in the fixed IRF
Δr´- the length interval in the moving IRF
In the following, all the notations with acute accent (´) will be related to the moving IRF.
Equations of mathematical physics
Generally, the apparatus of mathematical physics is presented by partial differential equations with initial and/or boundary conditions. The latter is formulating in accordance with a specific area of application (oscillations, electrodynamics, etc.). In the general case, such equations can be represented specifically in two-dimensional Euclidean space as [2]:
F(x,y,u, ![]() ,…,
,…, ![]() ) = 0 (4)
) = 0 (4)
where u (x, y) is required differentiable function.
As implementation of (4), in mathematical physics distinguish hyperbolic, parabolic and elliptic types of equations. The first two types are presented accordingly with:
1. The wave equation:
![]() = a2
= a2 ![]() (5)
(5)
that describes oscillatory processes in physical agents,
2. The heat propagation equation:
![]() = b2
= b2 ![]() (6)
(6)
that describes the processes of heat propagation in physical agents.
Below, these equations are studied under using LR with displacement into the moving IRF.
Substituting of Lorentz Transformations
Note the differential entries in equations (5-6) can be taken in account as small increments. Then regarding (2-3) in accordance with the principle represented in [4] we obtain:
∂t = ∂t´/ γ (7)
∂x = γ·∂x´ (8)
∂y = γ·∂y´ (9)
So in the moving IRF, the equations (5) and (6) can be written in the following form:
1) of the wave equation:
![]() = a´ 2
= a´ 2 ![]() (10)
(10)
where
a´= a / γ2 (11)
2) of the heat propagation equation:
![]() = b´ 2
= b´ 2 ![]() (12)
(12)
where
b´ = b / γ3/2 (13)
The expressions (10-13) show the principle, which can be used for determination of coefficients of partial differential equation of any order by use of Lorentz transformation.
Heat propagation equation in the moving IRF
Consider equation (6) in connection with a classical problem of heat distribution with the initial condition [2]:
u(x,0) = δ(x) (14)
where δ(x) is the Dirac delta function.
The standard solution to this problem is given in terms of the core of the equation (6).
Φ(x,t) =![]() exp(-x2/4b2 t) (15)
exp(-x2/4b2 t) (15)
In the moving IRF, this expression will use the value b´ from (13):
Φ(x,t) =![]() exp(-x2/4b´ 2 t) (16)
exp(-x2/4b´ 2 t) (16)
It means that the core of the heat propagation equation depends parametrically on LF.
In the Fig. 1, as an indication of this dependence, the curves of the function (16) for various values of LF (specifically by t = 1 and b = 0.75) are presented.
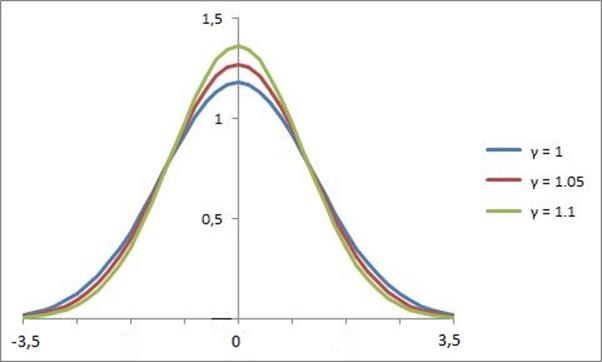
Fig. 1 The heat distribution in the rod in dependence on LF
Note the curves in Fig. 1 are similar to a Gaussian random process [5]. Under this analogy, we can assert that an increase of LF and thus the speed of the moving IRF leads to the decrease in the dispersion of heat distribution. Presumably, this statement is also valid in a more general formulation. However, proof of this is outside the scope of this article.
Wave equation in the moving IRF
As a specific case of a wave equation, consider the oscillations of a string with the fixed ends, while this string is directed along the vector of the moving IRF. Such a formulation of the problem leads to the equation (5) with boundary conditions. The solution to this equation for a string of the length r is normally represented with Fourier series, where the first element corresponds to the frequency of fundamental tone of the oscillation. This frequency is determined as:
Ω = πa / r (17)
in the fixed IRF, and
Ω` = πa`/ r` (18)
in the moving IRF.
From (18) in regard to (3) and (11) we obtain:
Ω` = (πa/γ2) / (r/γ)= πa/ γr (19)
Finally, the equations (17) and (19) imply an important ratio:
Ω` = Ω / γ (20)
Since γ > 1, it leads to the assertion that in the moving IRF the oscillation frequencies of a string decrease by a factor of γ, compared to the fixed IRF.
Some consequences, arising from this phenomenon are discussed below on specific examples.
Discussion
One of the consequences of the Special relativity is the so called “redshift” of the light spectrum [3]. In the paper [4], this effect was also stated in respect of oscillation generated by electric circuits. At the same time, in solution to the partial differential equation for a string with fixed ends, should be distinguished another interesting feature which is connected not only with the redshift only, but actually with the compression of the frequency spectrum.
Consider in the fixed IRF the set of strings with the fundamental tone frequencies Ω 1 < Ω 2 <…. <
Ωn .
Then in the moving IRF we obtain:
Ω`m - Ω`k = Ωm/γ – Ωk/γ = (Ωm – Ωk)/γ (21)
where m > k .
Thus, in the moving IRF, the intervals between fixed frequencies are reduced by the factor of γ compared with the fixed IRF. Note this kind of spectrum compression should not be confused, for example, with the psychoacoustic compression in the spectral area which is aimed to reduce the flow rate while maintaining the quality of a playback [6].
Next, we can imagine a guitar that is “tuned” in the fixed IRF in accordance with the intervals of the harmonic series [7]. Thereafter, this guitar is displacing into the moving IRF. With that action, as a result of relativistic compression of the spectrum (defined above, however with all other things being equal) the guitar will be “detuned”. The degree of such a detuning depends on LF, which in turn is connected with the speed of the moving IRF. For example, by the redshift on 1 Hz the speed of the moving IRF should be estimated as about 6.7% of the speed of light in a vacuum.
Conclusion
Above, the use of Lorentz transformations in some problems of mathematical physics was considered. Thus, with substituting of Lorentz ratios into partial differential equations, the equation coefficients will parametrically depend on the Lorentz factor value and thus on the relative speed of inertial reference frame in which physical processes are taking place. Further, this dependence is expressed in solution of partial differential equations. It is shown that for the heat propagation equation the relativistic decrease in the dispersion of heat occurs. In the case of a string oscillation equation, the oscillation fundamental frequency decreases by analogy with the redshift of the light spectrum. At the same time relativistic compression of the frequency spectrum occurs, which leads to a reduction in the intervals between the fixed frequencies, for example, in case of harmonic series.
Finally, although only second order differential equations were considered above, the represented approach can easily be extended to higher spatial order.
Ц(x,t) =![]() exp(-x2/4b2 t)
exp(-x2/4b2 t)
References
- Сучилин В. А. Relativistic Time Dilation Impact on Dynamics and Stability of Linear Systems // Современные научные исследования и инновации. 2018. № 2 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2018/02/85729
- Ильин А. Уравнения математической физики. Litres, 2017 – 193 с.
- Forshaw Jeffrey, Smith Gavin. Dynamics and relativity. John Wiley & Sons, 2014 – 344 p.
- Сучилин В.А. Relativistic Time Dilation Impact on Dynamics and Stability of Linear Systems // Современные научные исследования и инновации. 2018. № 2 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2018/02/85729
- Oliver C. Fundamentals of Applied Probability and Random Processes. Academic Press, 2005 – 456 p.
- Jayant, Nikil; Johnston, James; Safranek, Robert (October 1993). “Signal Compression Based on Models of Human Perception”. Proceedings of the IEEE. 81 (10): 1385–1422.
- Wikipedia: Harmonic series (music) [Электронный ресурс]. URL: https://en.wikipedia.org/wiki/Harmonic_series_(music)
