Маложесткие валы – ответственные элементы технологического оборудования, определяющие эффективность его эксплуатации. На основе изучения конструкций технологического оборудования текстильной отрасли машиностроения выявлен большой класс маложестких деталей широкой номенклатуры типа “вал”: валы сплошные и полые, шпиндели, валы оригинальной конструкции прядильного оборудования (вытяжные цилиндры, мотальные, плющильные валы и др.). Их количество на одну прядильную машину составляет до 170 единиц. Опыт эксплуатации и анализ отказов технологического оборудования прядильных производств показывает, что до 30 % отказов по количеству и до 60 % по времени простоя приходится на маложесткие валы [1, 2]. Замена вышедших из строя маложестких валов связана с демонтажем валов, а также сопрягаемых узлов и деталей, с полной или частичной потерей работоспособности оборудования. Наибольшее число отказов машин при этом связано с поломками узла валов малой жесткости, в частности в зоне их соединения. Обеспечение работоспособности валов малой жесткости представляет собой весьма актуальную задачу, особенно в условиях массового производства технологического оборудования.
Максимально возможные величины нагрузок в соединении соответствуют режимам пуска и останова машин, и определяют характер крутильных деформаций элементов соединения. Для анализа надежности работы соединения проведено исследование напряжений, возникающих в наиболее податливых элементах соединения камеры 1 и стержня (хвостовик) 2 (рисунок 1).
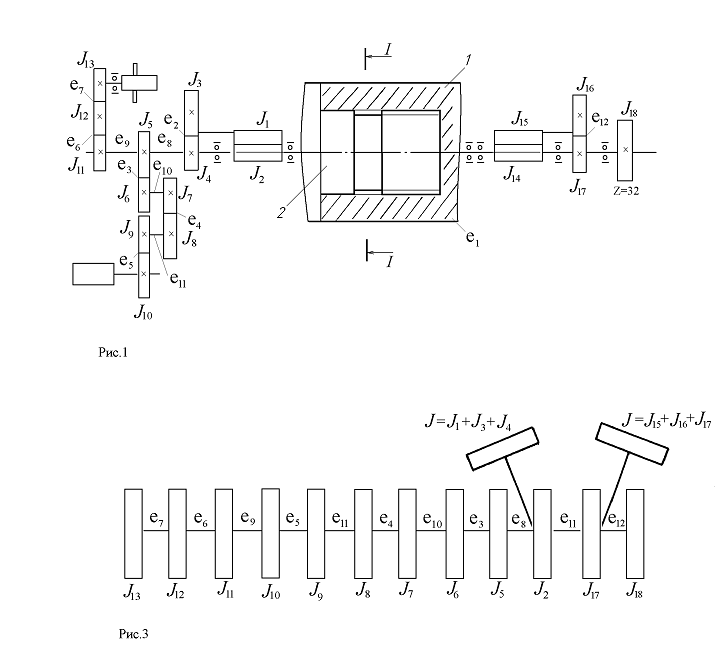
Рисунок 1. Кинематическая схема привода маложестких валов
Исследования выполнены на основе расчетной схемы в виде двухмассной модели (рисунок 2).
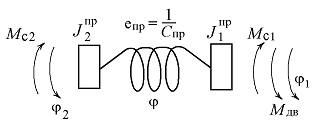
Рисунок 2. Расчетная динамическая модель узла ВМЖ
Модель получена последовательным приведением инерционных Ji и упругих еi (рисунок 3) параметров реальной кинематической цепи (рисунок 1) с сохранением значений потенциальной и кинетической энергий [2].
Рисунок 3. Эквивалентная схема замещения
Рассматриваемая модель обладает двумя степенями свободы и для ее исследования используем уравнения Лагранжа II рода
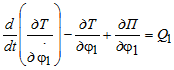
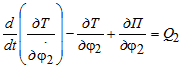
Кинетическая и потенциальная энергии системы определятся так
.gif)
![]() .
.
Беря соответствующие производные и используя уравнения Лагранжа, получим следующую систему дифференциальных уравнений
![]()
![]() , (1)
, (1)
где Мдв – момент двигателя, Н∙м; ![]() и
и ![]() – моменты сопротивления, Н∙м.
– моменты сопротивления, Н∙м.
Определим собственные частоты и формы колебаний, которые, как известно, не зависят от внешних факторов, поэтому систему уравнений (1) рассматриваем однородной, т.е.
![]()
![]() (2)
(2)
Решение полученной системы находим в форме
![]()
![]()
Подставляя это решение во (2) получим
![]()
![]() (3)
(3)
Система не будет иметь нулевого решения (при нулевом решении ![]() , что соответствует ее равновесию) в том случае, когда ее определитель равен 0.
, что соответствует ее равновесию) в том случае, когда ее определитель равен 0.
.gif)
Раскрывая его, получаем характеристическое уравнение, из которого определяем собственные частоты
![]() ;
; .gif) 4376 рад/с = 696, 82 Гц.
4376 рад/с = 696, 82 Гц.
Период свободных колебаний Тс = 1,435∙10-3 с.
Поскольку время изменения пускового и тормозного моментов (Мп, Мт), согласно исследованиям [3] составляет 0,30,4 с то исследуемая двухмассная модель может быть отнесена к числу высокочастотных.
Нулевому корню соответствует равномерное вращение системы как жесткого механизма. Корню 1 соответствуют гармонические колебания масс с моментами инерции ![]() и
и ![]() , сопровождающиеся деформацией упругого элемента. При определенных частотах система уравнений будет тождеством, то есть имеет множество решений, поэтому определитель этой системы позволяет найти отношение амплитуд (формы колебаний).
, сопровождающиеся деформацией упругого элемента. При определенных частотах система уравнений будет тождеством, то есть имеет множество решений, поэтому определитель этой системы позволяет найти отношение амплитуд (формы колебаний).
При = 0 = 0 ![]() .
.
При = 1 ![]() .
.
Отрицательное отношение ![]() означает, что при свободных колебаниях с частотой 1 массы
означает, что при свободных колебаниях с частотой 1 массы ![]() и
и ![]() колеблются в противофазах. Общее решение системы (2) будет описываться уравнениями
колеблются в противофазах. Общее решение системы (2) будет описываться уравнениями
![]()
.gif)
То есть крутильная деформация в зоне соединения будет оцениваться углом поворота сечения I-I (рисунок 1), который определяется так
.gif) .
.
Тогда скручивающий момент, воспринимаемый соединением (![]() ) будет равен
) будет равен
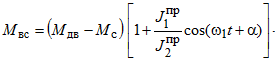
Значение моментов (![]() и
и ![]() ) были рассчитаны по известным формулам [3] для окружных скоростей маложестких валов 220 и 410 м/мин при пуске и торможении.
) были рассчитаны по известным формулам [3] для окружных скоростей маложестких валов 220 и 410 м/мин при пуске и торможении.
Установлено, что максимальное значение момента в соединении соответствует окружной скорости 220 м/мин и составляет 5,33 Н∙м.
Графики изменения скручивающих моментов изображены на рисунке 4.
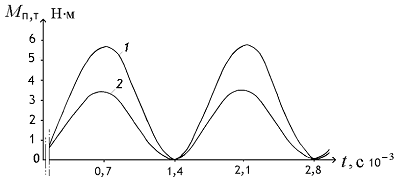
Рисунок 4 – Графики изменения момента в соединении ВМЖ
Кривые показывают, что амплитудные значения момента уменьшаются при увеличении скорости по зависимости, близкой к параболической. Цикл изменения момента соответствует собственной частоте крутильных колебаний. За время торможения машины (без учета демпфирования) соединение воспринимает до 200 крутильных колебаний. В данных условиях касательные напряжения в соединении превышают допустимые значения.
С учетом циклического характера нагрузки был определен требуемый коэффициент запаса прочности n ≈ 10 и допустимое значение касательного напряжения [] =2,07∙105 МПа.
Вывод. Для определения конструктивных параметров соединения маложестких валов на стадии проектирования целесообразно определение динамических усилий и колебаний, возникающих в соединении. Исследования крутильных колебаний в первом приближении может быть выполнено с использованием двухмассной расчетной модели.
Библиографический список
- Шорин В.А. Повышение работоспособности валов малой жесткости// Сб. V Междунар. научн. – техн. конф. «Точность и надежность технологических и транспортных систем». – Пенза, 1999.
- Шорин В.А. Комплексное обеспечение точности и работоспособности валов малой жесткости: дисс. канд. техн. н. – Пенза. – 2000. – 250 с.
- Длоугий и др. Приводы машин: справочник. – Л: Машиностроение, 1982. – 383.с.
