Introduction
In [1] it was shown that the relativistic time dilation impact on linear dynamical systems does not lead to the loss of stability, but at the same time reduces the stability margin of the system. At the same, linear systems consist of elements that are in itself an idealization of real nonlinear components. On the other hand, there are intrinsically nonlinear systems. So it is also important to consider the relativistic time dilation impact on the stability of nonlinear dynamical systems.
Recall, in accordance with special relativity the time dilation is a difference between the clock times, measured by two observers, one of which is in the moving inertial reference frame (IRF), and the other in the IRF, which is stationary relative to the first [2]. This time dilation is expressed by the Lorentz transformation:
Δt~ = γ·Δt (1)
where
Δt~ - time interval measured in the moving IRF
Δt – time interval measured in the stationary IRF
γ - Lorentz factor, γ = 1 /![]()
v – relative velocity of the moving IRF
c – light velocity in free space.
Thus, by definition the value of the Lorentz factor is equal to one for stationary IFR and greater than one for moving IRF.
Next, the notations with the upper tilde (~) will refer to the moving IRF.
Nonlinear system representation in the moving IRF
A nonlinear dynamical system may be formally described by means of nonlinear differential equation, where at least one the derivative of the calculated function (including the zero-order derivative, which actually is the calculated function itself) enters into the equation as a nonlinear factor [3]. Thus, the nonlinear differential equation has the following form:
an y(n)(t) + an-1 y(n-1)(t) + … āky(k)(t) … +aоy(t) = 0 (2)
where вk is one of the function f(y) or f(y(k)), that are relating to two types of the equation.
Under consideration of (1), i.e. in the moving IRF, equation (2) takes the form [1]:
an~y(n)(t) + an-1~y(n-1)(t) + … āk~y(k)(t) … +aо~y(t) = 0 (3)
where
an~ = гn an (4)
As for the element вk~, its representation is similar to (4) as
āk~ = гk f(y) (5)
for the first type
or
āk~ = гk f(гky(k)) (6)
for the second type, and г is Lorentz factor.
Note, that by г=1 in (3) it follows an~ = an.
Generally, for the nonlinear differential equations there are no useable analytical solution methods with exception to some particular cases [3]. Therefore, to study stability of a nonlinear dynamical system we will use numerical approach. Specifically Van der Pol’s and Rayleigh’s non harmonic oscillators [4] are considered, which are described by nonlinear second-order differential equations of the first and second type, respectively. Moreover, the estimation of stability is carried out by using the phase portrait techniques [5].
Van der Pol’s oscillator in the moving IRF
The Van der Pol’s oscillator is formally represented with the nonlinear differential equation of the second order related to the first of the types mentioned above:
y‘‘(t) + f(y) y’(t) + ?2 y(t) = 0 (7)
where ? is the oscillation frequency, and the nonlinear factor is expressed by the equality
f(y) = α (1 – y2) (8)
where α as a fixed parameter.
Further, in accordance with the quotients (4) and (5), and under consideration (8), the equation of the oscillator specifically in the moving IRF takes the form:
г2 y’’(t~) + α (1 – y(t~)2) γ y’(t~) + ?2 y(t~) = 0 (9)
or after reducing:
y’’(t~) + αо (1 – y(t~)2) y’(t~) + βо y(t~) = 0 (10)
where
αо= α/γ
βо= ?2/γ2
and γ is Lorentz factor.
Let us call (9) as Van der Pol’s equation in the generalized form, which takes into account the Lorentz factor.
By numerically study of the relativistic time dilation impact on the stability of Van der Pol’s oscillator, the following values of the fixed parameters were used: α=0.025 and ?2=1.
The results of computer simulation for different values of Lorentz-factor and under initial conditions y(0)=0 and y’(0)=1 are presented in the Table below.
Table 1. The stability of Van der Pol’s oscillator vs Lorentz factor
| Lorentz factor |
Oscillator phase portrait |
Type of bifurcation |
|
γ = 1.0 |
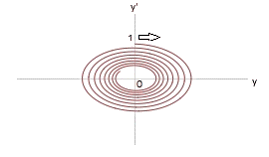 |
Steady focus (stationary IRF) |
|
γ = 2.0 |
 |
Stable limit cycle (moving IRF) |
|
γ = 2.5 |
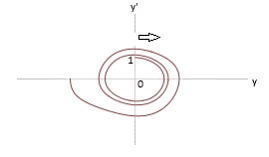 |
Unsteady focus (moving IRF) |
The Table above illustrates the feature of a nonlinear system that can be formulated as follows: upon transition to the mobile IRF, the nonlinear system, which is stable in the stationary IRF (γ=1.0), for other values of the Lorentz factor (γ>1) may go to the mode of stable limit cycle or become unstable. Moreover, this feature also depends on the initial conditions.
Rayleigh’s oscillator in the moving IRF
Similar to Van der Pol’s oscillator considered above, Rayleigh’s oscillator is represented by nonlinear differential equation of the second order related to the second the type with the nonlinear factor which contains the derivative of the calculated function:
f(y‘) = α (1 – y‘2) (11)
where α as a fixed parameter.
Thus, after reducing, the Rayleigh’s equation takes the form:
y’’(t~) + αо(1 – γ2 y‘2(t~)) y’(t~) + βоy(t~) = 0 (12)
where
αо= α/γ
βо=ꙍ2/γ2
(γ is Lorentz factor and ꙍ is the oscillation frequency) .
Let us call (12) as Rayleigh’s equation in the generalized form, which takes into account the Lorentz factor.
By numerical study of the relativistic time dilation impact on the stability of the Rayleigh’s oscillator, the following values of the fixed parameters were used: α=0.05 and ꙍ2=4.75.
The results of computer simulation for different values of Lorentz-factor and under initial conditions y(0)=0 and y’(0)=1 are presented in the Table below.
Table 2. The stability of Rayleigh’s oscillator vs Lorentz factor
| Lorentz factor |
Oscillator phase portrait |
Type of bifurcation |
|
γ = 1.0 |
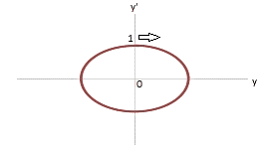 |
Stable limit cycle (stationary IRF) |
|
γ = 2.0 |
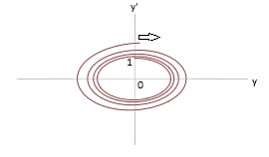 |
Unsteady focus (moving IRF) |
|
γ = 2.5 |
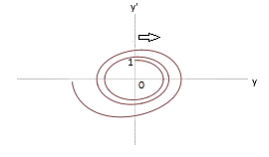 |
Unsteady focus (moving IRF) |
The Table above illustrates the feature of a nonlinear system, that can be formulated as follows: the nonlinear system, which stays in the mode of stable limit cycle in the stationary IRF (γ=1.0), may lose its stability by certain values of the Lorentz factor (γ>1) upon transition to the mobile IRF. Moreover, this feature also depends on the initial conditions.
Harmonic oscillator as a special case
As shown above, the stability of nonharmonic oscillators depends on Lorentz factor. From this point of view it is substantial to compare it to a harmonic oscillator.
Note that the nonlinear differential equation (7) may be easily reduced to the case of the harmonic oscillator while taking f(y) equal to a constant. So the numerical study here was produced with f(y)=0.05 and ꙍ2=4.75.
The results of the computer simulation under initial conditions y(0)=0 and y’(0)=1 are presented in the Table below.
Table 3. Stability of harmonic oscillator vs Lorentz factor
| Lorentz factor |
Oscillator phase portrait |
Type of bifurcation |
|
γ = 1.0 |
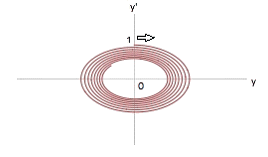 |
Steady focus (stationary IRF) |
|
γ =2.0 |
 |
Steady focus (moving IRF) |
|
γ = 2.5 |
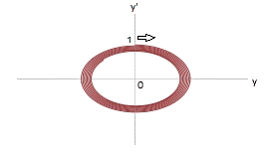 |
Steady focus (moving IRF) |
From the Table above follows that the linear system stays stable regardless of the value of Lorentz factor. Nevertheless, the stability margin is obviously diminishing as Lorentz factor increases (at the same time it is symptomatic, that the “density” of the oval pattern in the pictures above is increasing). That confirms our conclusion in [1], that stability of a linear dynamical system is invariant to the type of IRF, though the system stability margin (which is obviously related to the system response time) has a decreasing tendency.
Conclusions
It is shown above, that a nonlinear dynamical system as distinct from linear systems may become unstable in the moving inertial reference frame due to relativistic time dilation impact. On the other hand it is numerically confirmed that the linear dynamical systems stay stable regardless of the inertial reference frame, though the system stability margin is diminished. In addition, the formal representation of nonlinear dynamical systems and, in particular, Van der Pol’s and Rayleigh’s oscillators is generalized to the form which takes into account Einstein’s relativity.
References
- Soutchilin V. A. Relativistic Time Dilation Impact on Dynamics and Stability of Linear Systems // Современные научные исследования и инновации. 2018. № 2 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2018/02/85729
- Forshaw Jeffrey, Smith Gavin. Dynamics and relativity. John Wiley & Sons: 2014. 344p.
- Verhulst Ferdinand. Nonlinear differential equations and dynamical systems. Springer Science & Business Media: 2012. 306p.
- Mohazzabi Pirooz. Theory and examples of intrinsically nonharmonic oscillators. American Journal of Physics 72, 492 (2004)
- Terrell William J. Stability and Stabilization: An Introduction. Princeton University Press, 2009. 480p.
