Актуальность
С одной стороны, в своей работе [2] польский педагог Винценты Оконь озвучил и обосновал следующий тезис. Образование тем успешнее и тем больше развивает интеллект, чем больше ученик попадает на тот путь, по которому идёт учёный в ходе исследования.
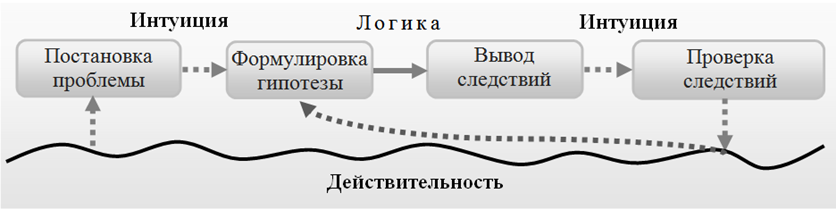
С другой стороны, эксперимент (проверка следствий) является решающим этапом полного цикла научного познания (рис.1).
Рисунок. 1. Полный цикл научного познания
Поэтому учителю следует периодически предлагать ученикам интересные и посильные задачи, решая которые, они будут экспериментировать.
Далее мы приводим пример такой задачи.
Задача о минимальном штрафе
Есть клетчатое поле. В каждой клетке указан штраф за её прохождение. Нужно пройти из левой верхней в нижнюю правую так, чтобы получить минимальный суммарный штраф. При этом из любой клетки разрешается шагать в клетку справа или снизу [3].
Напишите программу, которая считывает таблицу штрафов и находит минимальный суммарный штраф.
Точный алгоритм для задачи о минимальном штрафе. Динамическое программирование
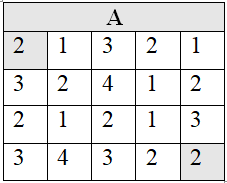
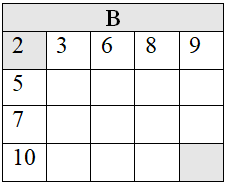
Для примера возьмём следующую таблицу штрафов.
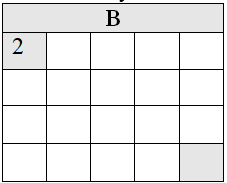
Заведём дополнительный двумерный массив B, размерами n на m. В него будем записывать решения подзадач. Пусть B[i,j] – это минимальный штраф от клетки (1,1) до (i, j).
Наша цель – найти B[n,m]. Заполняем массив постепенно.
Очевидно, есть один способ добраться до клетки (1,1). Штраф, который при этом придётся заплатить, равен числу, записанному в этой клетке. B[1,1]=A[1,1].
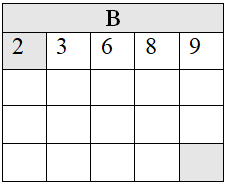
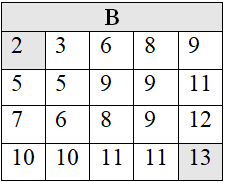
В любую клетку первой строки (1,j), кроме первой, можно прийти из клетки левее – из (1,j-1). Поэтому B[1,j]=B[1,j-1]+A[1,j]. По этой формуле вычисляем первую строку массива B.
В любую клетку первого столбца (i,1), кроме первой, можно прийти из клетки выше – из (i-1,1). То есть B[i,1]=B[i-1,1]+A[i,1]. По этой формуле находим первый столбец массива B.
В любую оставшуюся клетку можно шагнуть либо из клетки левее, либо из клетки выше – либо из (i, j-1), либо из (i-1,j). Выгоднее выбрать ту, где штраф минимален.
Значит, B[i,j]=min{B[i,j-1], B[i-1,j]}+A[i,j]. По этой формуле определяем оставшиеся элементы массива B. Строка за строкой.
Итак, минимальный штраф за весь путь хранится в клетке B[n,m] и равен 13 .
Приближенный алгоритм для задачи о минимальном штрафе. Муравьиный алгоритм
Алгоритм имитирует поведение колонии муравьёв [1, 4]. Колония муравьев легко находит кратчайший путь от муравейника к пище. Вначале муравьи двигаются произвольно. При этом оставляя за собой дорожки из особых веществ – феромонов. Нашедшие самый короткий путь к «кормушке» успевают по нему пробежать больше раз. Путь становится всё заметнее. Привлекает муравьев. Они всё чаще сворачивают на него. На остальных путях феромон постепенно испаряется и они исчезают. Через некоторое время, большинство муравьёв передвигаются по одному кратчайшему пути.
Как использовать этот факт для решения задачи? Запустим муравьев из первой клетки. И пусть они бегают по различным возможным маршрутам. На дешёвых оставляют больше феромона. На дорогих – меньше. Через некоторое время их остановим. Наилучший маршрут, который они найдут, и будем считать решением задачи.
Алгоритм.
1. Строим случайный маршрут. Считаем его наилучшим. Пусть Q – его стоимость.
2. Задаем начальный уровень феромона. Вводим ещё одну таблицу F, размерности n*m. Вначале в каждую её клетку записываем одно и то же небольшое положительное число. Поэтому при первом запуске муравьи будут двигаться произвольно, «не принюхиваясь».
3. Выбираем коэффициент испарения феромона p, из промежутка (0;1). Чем больше возьмём p, тем быстрее будет происходить испарение.
4. Повторяем k раз (k можно считать временем жизни муравьиной колонии).
4.1. Запускаем d муравьёв от стартовой клетки. Они пробегают до финиша. Для каждого находим маршрут и его стоимость.
Как муравей, путешествуя, определяет следующую клетку? По методу «рулетки». Возможным клеткам ставим в соответствие сектор рулетки. Чем больше феромона, тем больше сектор. Запускаем рулетку. Случай выбирает одну клетку. В неё и отправляется муравей.
4.2. Если какой-то муравей нашёл лучший маршрут, чем ранее, то запоминаем стоимость этого маршрута.
4.3. Увеличиваем феромон вдоль всех маршрутов, по которым прошли муравьи. Берём первого муравья, просматриваем клетки из его маршрута и на каждое добавляем феромон. По формуле F[i,j]:=F[i,j]+Q/L, где L – стоимость маршрута. Затем берём второго муравья и так далее. Тем самым, на лучших (дешёвых) маршрутах оставляем больше феромона.
4.4. Испаряем феромон во всех клетках. По формуле F[i,j]:=(1-p)*F[i,j]. Таким образом, постепенно удаляем клетки, которые меньше всего используются.
5. Выводим стоимость наилучшего маршрута.
Параметры p, k и d подбираем эмпирически.
Эксперимент
Первый муравьиный алгоритм был придуман в 1992 году. Не один десяток статей утверждает, что он достаточно быстро находит приближенное решение многих задач.
Проверьте на задаче о минимальном штрафе, насколько быстро муравьиный алгоритм находит её решение и насколько близко оно к точному.
Библиографический список
- Джонс М.Т. Программирование искусственного интеллекта в приложениях. М.:ДМК-Пресс, 2004.
- Оконь В. Основы проблемного обучения. М.: Просвещение, 1968.
- Окулов С. М. Программирование в алгоритмах. М.: БИНОМ. Лаборатория знаний, 2002.
- Штовба С.Д. Муравьиные алгоритмы // Exponenta Pro. Математика в приложениях. 2003. №4. с.70-75.