В работе рассматривается конвективный теплообмен и магнитная гидродинамика электропроводной жидкости, заключенной между двумя концентрическими сферами при отсутствии гравитационного поля. Задача описывается уравнениями теплообмена и магнитной гидродинамики: энергии, с учетом джоулевой диссипации; движения, с учетом электромагнитных, инерционных и вязких сил; магнитной индукции; неразрывности для скорости и магнитной индукции. Используется приближение Буссинеска.
Математическая постановка задачи в безразмерной форме имеет вид [1]:
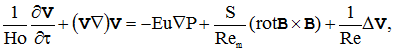 (1)
(1)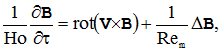
Задача (1)-(3) решалась в переменных вихрь (![]() ) функция тока (
) функция тока (![]() ) температура (
) температура (![]() ). Математическая постановка задачи в безразмерной форме в сферической системе координат с учетом симметрии по долготе имеет вид [1]:
). Математическая постановка задачи в безразмерной форме в сферической системе координат с учетом симметрии по долготе имеет вид [1]:
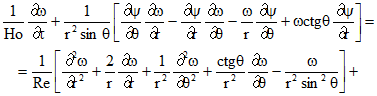
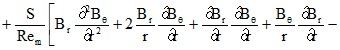 (4)
(4)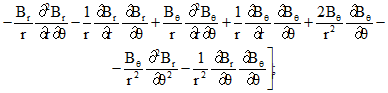
![]() ; (5)
; (5)
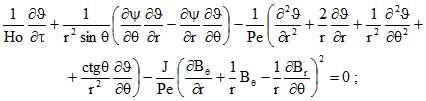 (6)
(6)
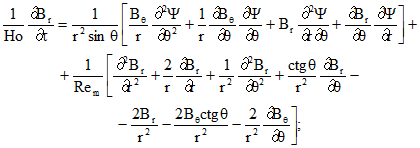 (7)
(7)
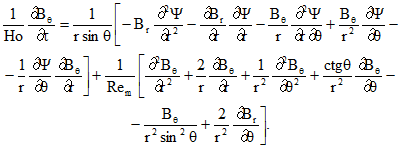 (8)
(8)
При проведении вычислительного эксперимента для температуры задавались граничные условия первого рода: значения температуры на внутренней Г1 (r = 1) и внешней Г2 (r = r2) поверхности сфер (внутренняя сфера более нагрета) ![]() .
.
Граничное условие для температуры на оси симметрии: .gif) .
.
Постоянная величина J, входящая в уравнение энергии (6), в зависимости от типа граничных условий для температуры принимает различные значения. Для граничных условий первого рода величина J определяется из выражения
Граничные условия для функции тока, напряженности вихря и магнитной индукции имели следующий вид:
.gif) ;
;Граничные условия для вихря на границах сферического слоя предполагают линейное изменение его по нормали [2].
Локальные числа Нуссельта на границе внутренней и наружной сферы рассчитывались по формулам:
.gif)
Осредненные числа Нуссельта вычислялись из соотношений:
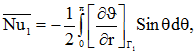
.gif)
Численное решение задачи осуществлялось с помощью метода конечных элементов. Алгоритм решения задачи представлен в [3]. В результате численного решения задачи были получены поля температуры, функции тока, напряженности вихря, радиальной и меридиональной составляющих магнитной индукции и распределения локальных чисел Нуссельта на внутренней и внешней поверхностях сферического слоя.
На рисунках 14 приведены стационарные результаты расчетов для следующих значений безразмерных критериев подобия:![]()
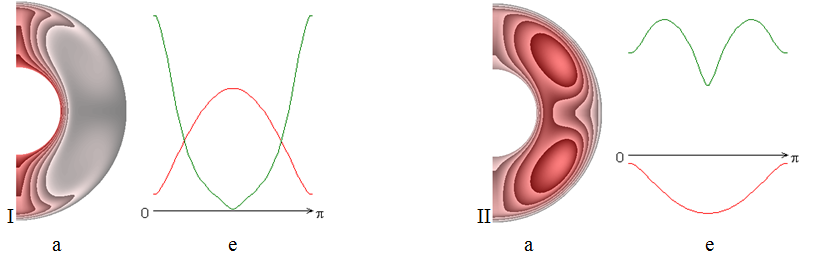
На рисунке 1 (I без учета теплоты джоулевой диссипации; II с учетом теплоты джоулевой диссипации) приведены результаты расчетов для числа Прандтля Pr=0,1.
При не учете теплоты джоулевой диссипации (рис. 1, I) теплообмен в слое осуществляется практически теплопроводностью. Значения локальных чисел Нуссельта (рис. 1, I, е; на внутренней поверхности слоя кривая красного цвета, на внешней зеленого) практически не отличаются от осредненных. Интенсивность теплообмена на внутренней поверхности слоя выше, чем на внешней. В слое образуются две конвективные ячейки (рис. 1, I, б) и четыре вихря (рис. 1, I, в).
В конвективной ячейке северного полушария жидкость движется против часовой стрелки (красный цвет, значения положительные), а южного – по часовой (синий цвет, значения отрицательные). Вихревая структура течения представлена двумя крупномасштабными вихрями вблизи внешней границы слоя и двумя мелкомасштабными вихрями вблизи внутренней границы слоя. Направления движения жидкости в крупномасштабных и мелкомасштабных вихрях противоположные. Значения радиальной составляющей магнитной индукции (рис. 1, I, г) в северном полушарии отрицательные, за исключением небольшой области у внутренней поверхности слоя (где они положительные), а в южном – положительные, за исключением небольшой области у внутренней поверхности слоя (где они отрицательные). Значения меридиональной составляющей магнитной индукции (рис. 1, I, д) положительные у внешней поверхности слоя и отрицательные у внутренней.
Учет теплоты джоулевой диссипации (рис. 1, II) приводит к значительным изменениям лишь поля температуры и распределения локальных чисел Нуссельта по сравнению с результатами, приведенными рис. 1, I. Структура течения жидкости и поле магнитной индукции практически не изменяются и поэтому не приводятся (оказалось, что такая тенденция имеет место и для других рассмотренных значений числа Прандтля Pr=1; 5; 50; 100). Механизм теплообмена в слое изменяется с кондуктивного на конвективный. Интенсивность теплообмена на внешней поверхности слоя выше, чем на внутренней. На внешней поверхности слоя значения локальных чисел Нуссельта положительные, а на внутренней отрицательные.
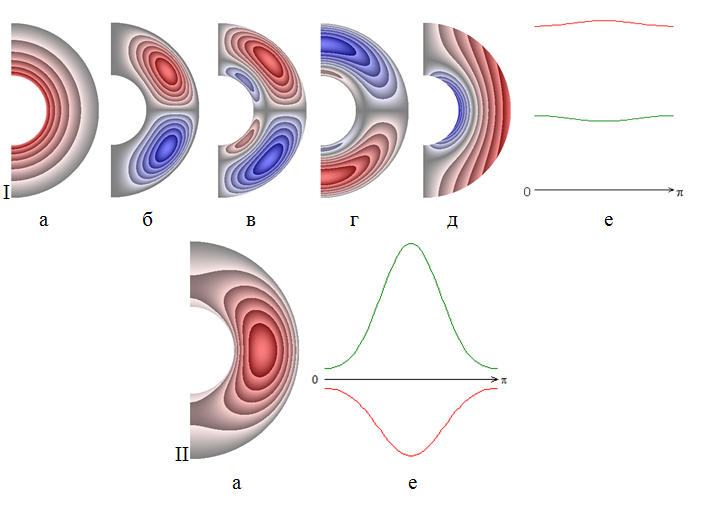
На рисунке 2 приведены результаты расчетов для числа Прандтля Pr=1.
При не учете теплоты джоулевой диссипации (рис. 2, I) теплообмен в слое уже осуществляется конвекцией (рис. 2, I, а) по сравнению с результатом, приведенным на рис. 1, I, а. Интенсивность теплообмена на внутренней поверхности слоя выше, чем на внешней.
Учет теплоты джоулевой диссипации (рис. 2, II) изменяет поле температуры (рис. 2, II, а), а интенсивность теплообмена на границах сферического слоя (рис. 2, II, е) изменяется на противоположную по сравнению с результатом рис. 2, I, е.
Интенсивность теплообмена на внешней поверхности слоя выше, чем на внутренней. На внешней поверхности слоя значения локальных чисел Нуссельта положительные, а на внутренней отрицательные (рис. 2, II, е).
Структура течения жидкости и поле магнитной индукции практически не изменяются по сравнению с результатами, представленными на рис. 1, I, б, в, г, д.
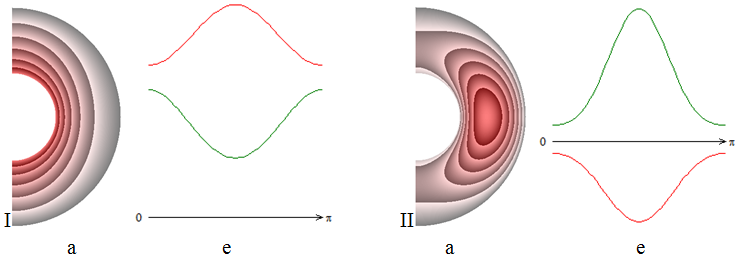
На рисунке 3 приведены результаты расчетов для числа Прандтля Pr=5.
Увеличение числа Прандтля приводит к дальнейшему изменению поля температуры и распределения чисел Нуссельта.
Как без учета теплоты джоулевой диссипации (рис. 3, I), так и с учетом (рис. 3, II) теплообмен в слое осуществляется конвекцией. Характер поведения локальных чисел Нуссельта качественно изменяется незначительно, но при не учете теплоты джоулевой диссипации (рис. 3, I, е) имеет место равенство значений локальных чисел Нуссельта на внутренней и внешней поверхностях в точках их пересечений.
Структура течения жидкости и поле магнитной индукции практически не изменяются.
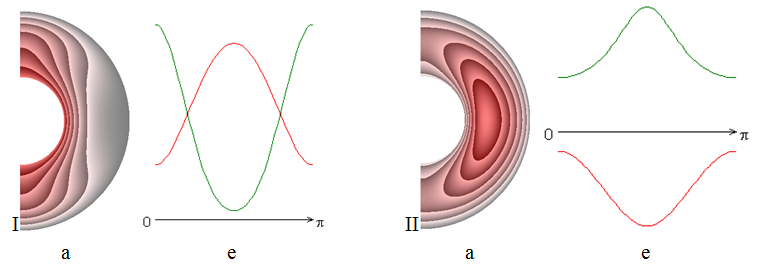
На рисунке 4 приведены результаты расчетов для числа Прандтля Pr=50.
Увеличение числа Прандтля приводит к дальнейшему значительному изменению поля температуры и распределения локальных чисел Нуссельта.
Как учет теплоты джоулевой диссипации, так и не учет ее (рис. 4, I и 4, II) значительно изменяет поле температуры и распределение локальных чисел Нуссельта при сравнении с предыдущими результатами. Особенно заметное изменение имеет место как для поля температуры (рис. 4, II, а), так и для распределения числа Нуссельта на внешней поверхности слоя (рис. 4, II, е) при учете теплоты джоулевой диссипации.
Структура течения жидкости и поле магнитной индукции практически не изменяются.
Оказалось, что увеличение числа Прандтля до 100 не приводит к изменению поля температуры, распределения локальных чисел Нуссельта, структуры течения жидкости и поля магнитной индукции.
Из анализа полученных результатов можно сделать следующие выводы:
при отсутствии гравитационного поля для всех рассмотренных режимов структура течения жидкости и поле магнитной индукции в сферическом слое сохраняются;
учет теплоты джоулевой диссипации оказывает значительное влияние на температурное поле жидкости в слое и распределение локальных чисел Нуссельта;
математическая модель и полученные результаты могут быть полезными при исследовании тепловых и магнитогидродинамических процессов в замкнутых объемах в условиях невесомости.
Библиографический список
- Булгаков В. К., Соловьев С. В. Модели тепловой конвекции в мантии и ядре земли. М.: Наука, 2001.
- Госмен А. Д., Пан В. М., Ранчел А. К., Сполдинг Д. Б., Вольфштейн М. Численные методы исследования течений вязкой жидкости, М.: Мир, 1972.
- Соловьев С. В. Моделирование конвективного теплообмена электропроводной жидкости в шаровой полости. Алгоритм решения. Инженерно-физический журнал. 2015. Т.88, № 6. С. 1370-1385.
