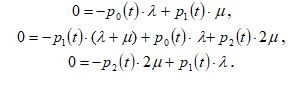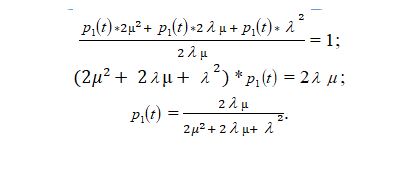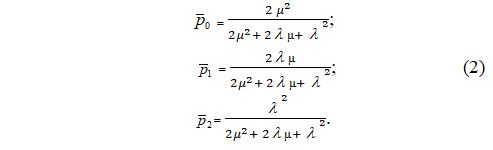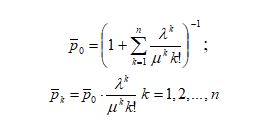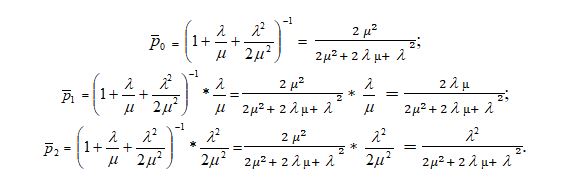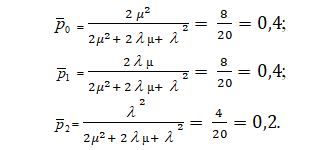Теория СМО посвящена разработке методов анализа, проектирования и рациональной организации систем, относящихся к различным областям деятельности, таким как связь, вычислительная техника, торговля, транспорт, военное дело.
Системы массового обслуживания – это такие системы, в которые в случайные моменты времени поступают заявки на обслуживание, при этом поступившие заявки обслуживаются с помощью имеющихся в распоряжении системы каналов обслуживания [1].
По числу каналов СМО подразделяют на одноканальные и многоканальные. СМО делят на два основных типа (класса): СМО с отказами и СМО с ожиданием (очередью) [2].
В данной статье рассматривается двухканальная СМО с отказами и ее вероятностные характеристики, а именно вероятности состояний как функции времени и их финальные вероятности.
Сначала построим математическую модель системы. Выделим состояния двухканальной СМО с отказами:
S₀ – в СМО все каналы свободны (нет заявок);
S₁ – в СМО занят один канал, второй канал свободен (1 заявка);
S₂ – в СМО заняты оба канала (2 заявки).
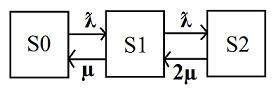
Схема двухканальной СМО с отказами приведена на рисунке 1. Поток заявок с интенсивностью λ переводит систему из состояния S0 в состояние S1, из состояния S1 в состояние S2. Перевод системы из состояния S1 в состояние S0 осуществляет поток обслуживаний с интенсивностью μ. Перевод системы из состояния S2 в состояние S1 осуществляет поток событий, который представляет собой сумму двух потоков обслуживаний обоих занятых каналов, каждый из которых имеет интенсивность μ. Сумма этих двух простейших потоков обслуживаний представляет собой также простейший поток интенсивностью 2μ.
Рис. 1. Схема двухканальной СМО с отказами
Составим математическую модель. Пользуясь графом состояний, запишем уравнения Колмогорова:
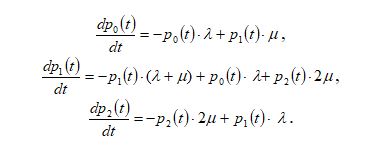Для нахождения финальных вероятностей приравняем к 0 производные в уравнениях Колмогорова:
Сложив все уравнения, получим верное равенство 0=0. Это значит, что уравнения линейно зависимы и одно из уравнений можно из системы удалить. Заменим второе уравнение уравнением нормировки:
Получим систему:
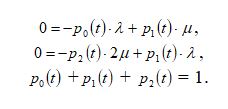Выразим из первого уравнения p0(t), из второго – p2(t) и подставим в третье уравнение:
Выразим из третьего уравнения p1(t):
И подставим в систему (1):
Для проверки полученного решения (2) воспользуемся формулами Эрланга:
Для данной системы получим:
Значения финальных вероятностей, полученных с помощью формул Эрланга, совпали со значениями (2). Следовательно, значения финальных вероятностей найдены верно.
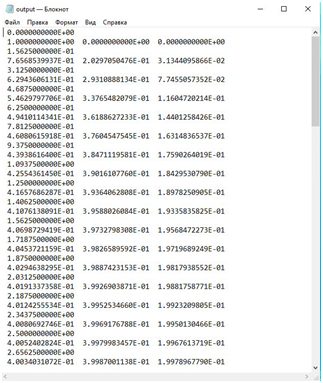
Для нахождения вероятности состояний как функции времени воспльзуемся средой Turbo Pascal. В учебнике Трубникова С.В. «Стохастические и имитационные модели» описана процедура, которая решает задачу Коши для системы из m обыкновенных дифференциальных уравнений 1 порядка на отрезке [a,b] методом Рунге-Кутта. Отрезок [a,b] разбивается на Nn равных частей и приближенное решение определяется в точках разбиения. Число Nn подбирается по правилу Рунге исходя из требуемой погрешности e. Начальные условия задаются в точке a. Исходные данные: a и b – координаты концов отрезка; e – требуемая точность; m – число уравнений в системе (1<=m<=100); значения m неизвестных функций в точке a (их необходимо поместить в файле input.pas до выполнения этой процедуры); f(p,x,u) – функция, задающая правые части дифференциальных уравнений (здесь p – номер дифференциального уравнения, x – независимая переменная, а u – массив зависимых переменных, обозначающих неизвестные функции) [3].
Результаты работы процедуры: приближенные значения неизвестных функций в последующих точках разбиения (они вычисляются и помещаются в файл output.pas); Флажок fl (он примет значение 1, если заданная точность достигнута, и 0 – в противном случае). В программе также описывается функция f(p,x,u) и вводятся значения необходимых исходных данных.
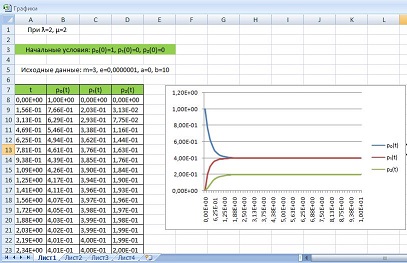
Для тестирования программы зададим интенсивности. Пусть λ= 2, µ = 2. Начальные условия: p0(t) = 1, p1(t) = 0, p2(t) = 0. Исходные данные: m=3, e=0,0000001, a=0, b=10. В файле output.pas появятся значения (рисунок 2).
Рис. 2. Тестирование программы
Проверим выполняется ли уравнение нормировки для t = 10:
p0(t) + p1(t) + p2(t) = 0,4+0,4+0,2=1 – верно.
При подстановке в формулы финальных вероятностей (2), значений λ= 2, µ = 2
Значения совпали. Тестирование программы прошло успешно.
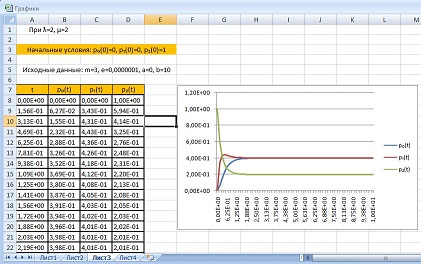
Реализуем компьютерную модель. Для этого перенесем данные, полученные в файле output.pas в табличный процессор Excel для всех возможных начальных условий:
1) p0(t) = 1, p1(t) = 0, p2(t) = 0;
2) p0(t) = 0, p1(t) = 1, p2(t) = 0;
3) p0(t) = 0, p1(t) = 0, p2(t) = 1
И построим графики по получившимся таблицам. Для каждого случая компьютерная модель изображена на рисунке 3, 4, 5 соответственно.
- Рис. 3. Компьютерная модель для начальных условий 1)
- Рис. 4. Компьютерная модель для начальных условий 2)
- Рис. 5. Компьютерная модель для начальных условий 3)
Из графиков видно, что вероятность состояния, в котором первоначально была система, с увеличением t уменьшается до определенного уровня, затем стабилизируется (вероятность становится финальной). В остальных же состояниях с увеличением t вероятности увеличиваются, затем также стабилизируются. Суммы вероятностей всех состояний на протяжении всего времени остаются равны единице.
Библиографический список
- Электронное учебное пособие «Имитационное моделирование экономических процессов» [Электронный ресурс]. URL:http://eos.ibi.spb.ru/umk/11_4/5/5_R0_T6.html (дата обращения: 7.06.2016).
- Математический форум Math Help Planet [Электронный ресурс]. URL: http://mathhelpplanet.com/static.php?p=sistema-massovogo-obsluzhivaniya (дата обращения: 5.06.2016).
- Трубников С.В. Стохастические и имитационные модели: Учебное пособие для студентов вузов. – Брянск: «Курсив», 2012. – 206 с. (129с.)