Во многих областях практической деятельности человек сталкивается с необходимостью пребывания в состоянии ожидания. Подобные ситуации возникают в очередях, в супермаркетах, в крупных аэропортах, при ожидании обслуживающим персоналом самолетов разрешение на взлет или посадку, в пенсионном фонде. Во всех перечисленных случаях имеет место массовость и обслуживание. Изучением таких ситуаций занимается теория систем массового обслуживания.
Теория массового обслуживания составляет один из разделов теории вероятностей. В этой теории рассматриваются вероятностные задачи и математические модели. 
На основе теории массового обслуживания выбирается оптимальный вариант организации торгового обслуживания населения, обеспечивающий минимальное время обслуживания при минимизации затрат и высоком качестве обслуживания населения.
Предмет теории массового обслуживания – построение математических моделей, связывающих заданные условия работы системы массового обслуживания (СМО) (число каналов, их производительность, правила работы, характер потока заявок) с показателями эффективности СМО. Эти показатели описывают способность СМО справляться с потоком заявок. Ими могут быть: среднее число заявок, обслуживаемых СМО в единицу времени; среднее число занятых каналов; среднее число заявок в очереди и т.д.
Каждая СМО состоит из какого-то количества обслуживающих единиц, которые называются каналами обслуживания (это станки, транспортные тележки, роботы, линии связи, кассиры, продавцы и т.д.). Всякая СМО предназначена для обслуживания, какого-то потока заявок (требований), поступающих в какие-то случайные моменты времени.
По данным, полученным из работы магазина, установлено среднее количество покупателей в незагруженный период времени (с 9 ч до 16 ч) – 3-5 человек на кассу со средним временем обслуживания покупателя 4-6 минут, в загруженный период времени (с 16 ч до конца работы магазина) количество покупателей на кассу увеличивается до 8-10 человек со средним временем обслуживания 5-10 минут. В загруженный период времени работы магазина к кассе подходит 1 человек за 2 минуты, а в незагруженный – 1 человек в 6 минут. Полученные данные занесены в таблицу (табл. 1).
Необходимо решить задачи, используя основы математической теории массового обслуживания и найти оптимальный вариант организации торгового обслуживания, при котором время обслуживания будет минимальным, качество высоким и затраты минимальный.

Таблица 1 – Исходные данные работы магазина

	1 касса	2 кассы	3 кассы	4 кассы	5 касс
Количество покупателей в незагруженный период времени	4 чел.	4 чел.	3 чел.	4 чел.	5 чел.
Количество покупателей в загруженный период времени	9 чел.	8 чел.	9 чел.	8 чел.	10 чел.
Среднее время обслуживания покупателя в незагруженный период времени	5 мин.	6 мин.	6 мин.	4 мин.	4 мин.
Среднее время обслуживания покупателя в загруженный период времени	8 мин.	10 мин.	10 мин.	6 мин.	5 мин.

Решение одноканальной СМО с неограниченной очередью в незагруженный период времени
Система массового обслуживания – одна касса с неограниченной очередью. Поток клиентов простейший. В среднем к кассе приходит 1 покупатель за 6 минут. Кассир в среднем обслуживает 1 покупателя за 5 мин. Необходимо вычислить среднее время пребывания заявки в системе и среднее время пребывания заявки в очереди. 
Решение. Имеется система массового обслуживания с одним каналом (одна касса) и неограниченной очередью. Интенсивность потока входящих заявок равна (1 покупатель за 6 минут) = (10 покупателей в час), то есть . Интенсивность потока обслуживания равна (1 покупатель за 5 минут) = (12 покупателей за час), то есть .
Нагрузка системы ,, поэтому предельный режим работы системы существует. Рассчитаем эффективность работы СМО в предельном режиме. 
Среднее число заявок, находящихся в очереди (покупателейв очереди) равно:
.
Среднее время ожидания в очереди равно:
.
Среднее число обслуживаемых покупателей равно: .
Среднее время обслуживания равно: .
Тогда среднее число заявок в системе: .
Среднее время пребывания заявки (покупателя) в системе:
.
Решение одноканальной СМО с неограниченной очередью в загруженный период времени
Система массового обслуживания – одна касса с неограниченной очередью. Поток клиентов простейший. В среднем к кассе приходит 1 покупатель за 2 минуты. Кассир в среднем обслуживает 1 покупателя за 7,5 мин. Необходимо вычислить среднее число заявок в системе и в очереди, среднее время пребывания заявки в системе и среднее время пребывания заявки в очереди. 
Решение. Имеется система массового обслуживания с одним каналом (одна касса) и неограниченной очередью. Интенсивность потока входящих заявок равна (1 покупатель за 2 минуты) = (30 покупателей в час), то есть . Интенсивность потока обслуживания равна (1 покупатель за 7,5 минут) = (8 покупателей за час), то есть .
Нагрузка системы . Поскольку , то очередь будет расти бесконечно, следовательно, предельных вероятностей не существуют. СМО не будет работать в стационарном режиме. Поэтому необходимо ввести еще один канал или уменьшить время обслуживания.
Решение многоканальной СМО с неограниченной очередью в незагруженный период времени
Система массового обслуживания – пять касс с неограниченной очередью. Поток клиентов простейший. В среднем к кассе приходит 1 покупатель за 6минут. Кассир в среднем обслуживает 1 покупателя за 5 минут. Необходимо вычислить среднее число заявок в системе и в очереди, среднее время пребывания заявки в системе и среднее время пребывания заявки в очереди. 
Решение. Имеется система массового обслуживания с пятью каналами (пять касс) и неограниченной очередью. Интенсивность потока входящих заявок равна (1 покупатель за 6 минут) = (10 покупателей в час), то есть . Интенсивность потока обслуживания равна (1 покупатель за 5 минут) = (12 покупателей за час), то есть .
Нагрузка системы , , поэтому предельный режим работы системы существует.
Среднее число обслуживаемых покупателей равно: .
Среднее время обслуживания равно: .
Среднее число касс, занятых обслуживанием: .
Среднее число простаивающих касс: .
Коэффициент занятости каналов обслуживанием: .
Следовательно, система на 20% занята обслуживанием.
Абсолютная пропускная способность:
.
Вероятность образования очереди: .
Среднее число заявок (покупателей), находящихся в очереди:
.
Среднее время ожидания в очереди равно: .
Тогда среднее число заявок (покупателей) в системе:
.
Среднее время пребывания заявки в системе: .
Решение многоканальной СМО с неограниченной очередью в загруженный период времени. 
Система массового обслуживания – пять касс с неограниченной очередью. В среднем к кассе приходит 1 покупатель за 2 минуты. Кассир в среднем обслуживает 1 покупателя за 7,5 мин. Необходимо вычислить среднее число заявок в системе и в очереди, среднее время пребывания заявки в системе и среднее время пребывания заявки в очереди. 
Решение. Имеется система массового обслуживания с пятью каналами (пять касс) и неограниченной очередью. Интенсивность потока входящих заявок равна (1 покупатель за 2 минуты) = (30 покупателей в час), то есть . Интенсивность потока обслуживания равна (1 покупатель за 7,5 минут) = (8 покупателей за час), то есть .
Нагрузка системы, , поэтому предельный режим работы системы существует.
Среднее число обслуживаемых покупателей равно: .
Среднее время обслуживания равно: .
Вероятностьтого, что канал свободен:
.
Среднее число касс, занятых обслуживанием: .
Среднее число простаивающих касс: .
Коэффициент занятости каналов обслуживанием: .
Следовательно, система на 20% занята обслуживанием.
Абсолютная пропускная способность:
.
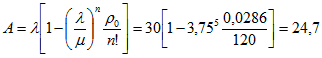Вероятность образования очереди:
.
Среднее число заявок (покупателей), находящихся в очереди:
.
Среднее время ожидания в очереди равно: .
Тогда среднее число заявок (покупателей) в системе:
.
Среднее время пребывания заявки в системе:
.
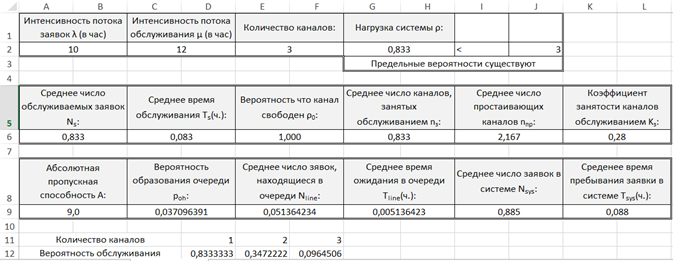
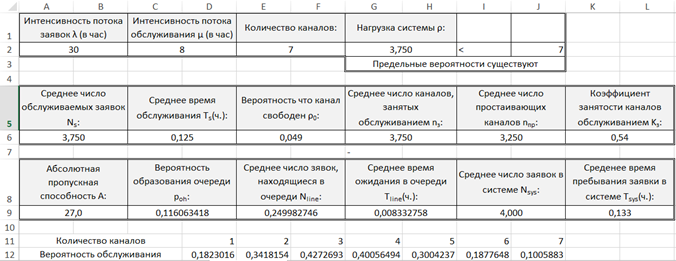
По вычисленным задачам можно сделать вывод, что оптимальное количество касс в незагруженный период времени равно 3, а минимальное время обслуживания – 5 минут (рис. 1), а в загруженный период времени – 7, минимальное время обслуживания – 7,5 минут (рис. 2).

1. Картошевский В.Г. Основы теории массового обслуживания. М., 2013.
2. Клейнрок Л.Н. Теория массового обслуживания. М, 2011.
3. Ложковский А.Г. Теория Массового обслуживания в телекоммуникациях. СПб, 2012.
4. Матвеев В.Ф.Системы массового обслуживания. М., 2012.

Все статьи автора «Якшибаев Ильдар Салаватович»