В традиционных методах моделирования объемов реализации услуг субъектов естественных монополий, факторы неопределенности либо не учитываются вообще, либо учитываются неявно, что в значительной степени приводит к неполноте и неадекватности учета этих факторов.
Как правило, природно-климатические факторы: температура воздуха, продолжительность светового дня, аномальные природные явления, являются источником неопределенности объемов реализации услуг субъектов естественных монополий [1].
Исходные данные, отражающие объемы реализации услуг и соответствующие значения природно-климатических факторов, можно описать линейной функциональной зависимостью. В процессе оценивания параметров функциональной зависимости для учета погрешности аргументов линейной функции – значений природно-климатических факторов и самой функции – объема реализации услуг можно использовать методы конфлюэнтного анализа [2].
Рассмотрим потребление электроэнергии населением региона  при изменении множества факторов. Предположим, что исходные данные, отражающие потребление электроэнергии населением Калужской области и соответствующие значения факторов, описываются многомерной линейной функциональной зависимостью [2]:

,

где  – параметры многомерной функциональной зависимости.
Модель оценивания параметров с учетом погрешностей, как значений функции , так и значений аргументов  имеет вид:

, ,

где  и  – случайные величины, характеризующие ошибки значений  и  соответственно;  – неизвестные (истинные) значения .
Предположим, что ошибки измерений  и  – нормально распределенные случайные величины с нулевыми средними значениями, с дисперсиями  и  соответственно.
Оценки параметров ,  находятся из условия минимума функционала

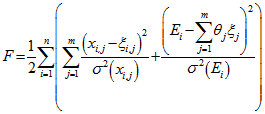. (1)

При нахождении минимума функционала (1) по параметрам  функции  неизвестны истинные значения абсцисс  экспериментальных точек, а известны лишь их доверительные интервалы. Поэтому, прежде чем проводить оценку параметров , определим . Истинные значения  определяем из условия:

, . (2)

Оценки параметров находят из следующего условия:

, .

При определении  необходимо следить за тем, чтобы значения  принадлежали области неопределенности измеренных величин . Когда случайные величины распределены по нормальному закону, требуется выполнение ограничения следующего вида:

,

где  – коэффициент, определяющийся, исходя из условия доверия.
Для линейной функциональной зависимости  из (2) получим  линейных алгебраических уравнений. Система (2) представляет  не связанных между собой систем из  линейных уравнений.
Практически сначала решается регрессионная задача нахождения оценок  при значениях , . Получают первое приближение для оценок . Затем определяют точные значения , при этом проверяется принадлежность новых значений  области возможных значений . Эти действия повторяют до тех пор, пока не выполнится одно из условий:
1) на очередном шаге значение функционала (1) меньше заданного числа ;
2) на соседних итерациях значение функционала (1) и значения оценок параметров  отличаются незначительно, т.е.

; , где  и  – заданные числа;

3) исчерпан лимит итераций.
В процессе оценивания объемов реализации услуг субъектов естественных монополий при случайном характере природно-климатических факторов необходимо получать не только точечные, но и интервальные оценки прогнозируемых показателей [3, 4], что повышает достоверность прогноза и, как следствие, снижает степень неопределенности и повышает эффективность принимаемых управленческих решений.
Исследования проведены при финансовой поддержке Российского фонда фундаментальных исследований и Правительства Калужской области (проект № 14-41-03085).

1. Гагарин Ю.Е., Гагарина С.Н., Гриценко Н.С., Зайцева Н.В., Степович М.А.Результаты моделирования объемов реализации услуг субъектов естественных монополий с учетом неопределенности информации. Труды регионального конкурса проектов фундаментальных научных исследований, 2015. Вып. 20.
2. Грешилов А.А. Математические методы принятия решений. М.: Изд-во МГТУ им. Н.Э. Баумана, 2006.
3. Гагарина С.Н., Гагарин Ю.Е. Интервальное прогнозирование объемов спроса на услуги субъектов естественных монополий с учетом неопределенности информации. Вестник университета (Государственный университет управления), 2013. № 22.
4. Гагарин Ю.Е., Гагарина С.Н., Гриценко Н.С., Зайцева Н.В., Степович М.А.Интервальные оценки как фактор повышения точности прогнозных расчетов при определении объемов реализации услуг. Труды регионального конкурса проектов фундаментальных научных исследований, 2016. Вып. 21.

Все статьи автора «Гагарин Юрий Евгеньевич»