Введение
При изучении атома водорода, с целью выявления всех тонкостей поведения электрона, одним из главных условий является применение правильных, адекватных уравнений. До последнего времени, для этого применялись уравнения Шредингера, Клейна-Гордона и Дирака. Уравнение Шредингера анализировать не будем, так как оно не релятивистское и поэтому не может претендовать на полное и точное описание в диапазоне высоких энергий и скоростей.
Далее будет показано, что и уравнение Клейна-Гордона тоже неприемлемо, по причине допущенной, глубоко замаскированной ошибки, при выводе этого уравнения.
Поскольку, в связи с поставленной целью, мы будем анализировать поведение электрона в состояниях с энергией ниже основного состояния, то будет показано, что в этой области к результатам решений уравнения Дирака тоже нужно относиться с неким подозрением.
В итоге, единственным приемлемым уравнением остается уравнение М2 [1].
Данную статью можно скачать в формате PDF по ссылке - https://portalnp.snauka.ru/wp-content/uploads/2016/06/ExoticHatom2.pdf
Анализ уравнений квантовой механики
В работе [1] приведен краткий вывод стационарного уравнения Клейна-Гордона (УКГ). Ключевой особенностью уравнения Клейна-Гордона является то обстоятельство, что оно отражает, в форме дифференциального уравнения, соотношение энергии и импульса Специальной Теории Относительности (СТО) ![]() (1.1)
(1.1)
Далее в работе [1] приводится аналитическое решение УКГ для изоэлектронного ряда водорода в основном состоянии. В результате решения получена формула для энергии основного состояния в следующем виде:
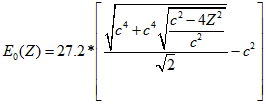 эВ (1.2) Сравнительный анализ полученных решений с экспериментальными данными показал, что по мере увеличения заряда ядра
эВ (1.2) Сравнительный анализ полученных решений с экспериментальными данными показал, что по мере увеличения заряда ядра ![]() отклонения сильно увеличиваются. Посмотрев на формулу (1.2) можно заметить, что под квадратным корнем находится выражение:
отклонения сильно увеличиваются. Посмотрев на формулу (1.2) можно заметить, что под квадратным корнем находится выражение: ![]() Следовательно можно записать
Следовательно можно записать ![]() откуда следует неравенство
откуда следует неравенство ![]() (1.3) где
(1.3) где ![]() заряд ядра водородоподобного иона,
заряд ядра водородоподобного иона, ![]() скорость света в атомных единицах Хартри. Следовательно из неравенства (1.3) получим
скорость света в атомных единицах Хартри. Следовательно из неравенства (1.3) получим ![]() . А это означает, что при превышении заряда ядра
. А это означает, что при превышении заряда ядра ![]() решения УКГ срываются и под квадратным корнем получается отрицательное значение.
решения УКГ срываются и под квадратным корнем получается отрицательное значение.
Приведенный расчет доказывает ошибочность уравнения Клейна-Гордона, так как такая ситуация должна была случиться при ![]() а не при
а не при ![]() .
.
Теперь посмотрим по какой причине возникла данная ошибочная ситуация и к чему приведет устранение этой ошибки.
Когда при выводе уравнения Клейна-Гордона, в выражение связи энергии и импульса СТО (1.1) подставляем выражение квадрата импульса через волновую функцию ![]() то думаем, что получили релятивистский квадрат импульса. То есть думаем что
то думаем, что получили релятивистский квадрат импульса. То есть думаем что 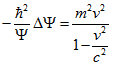 (вернее так думали Клейн и Гордон при выводе уравнения).
(вернее так думали Клейн и Гордон при выводе уравнения).
Но на самом деле, уравнение воспринимает выражение ![]() (1.4) как обычный квадрат импульса
(1.4) как обычный квадрат импульса ![]()
Почему так? Оставим этот вопрос глубоким теоретикам. А нас интересует практическая сторона вопроса. То есть устранение ошибки в уравнении Клейна-Гордона.
Одним словом, релятивистский квадрат импульса не определяется выражением ![]() . И поэтому получаем ошибочное уравнение Клейна-Гордона.
. И поэтому получаем ошибочное уравнение Клейна-Гордона.
Теперь, если переписать выражение (1.1) в развернутом виде .gif) и сделать необходимые преобразования:
и сделать необходимые преобразования: .gif) и подставить уже обычный квадрат импульса
и подставить уже обычный квадрат импульса ![]() на свое место. То получим:
на свое место. То получим: .gif) (1.5). Переписав выражение (1.5) в удобной форме получим:
(1.5). Переписав выражение (1.5) в удобной форме получим: ![]() (1.6), что соответствует выражению (2.5) в статье “Новое уравнение релятивистской квантовой механики” [1].
(1.6), что соответствует выражению (2.5) в статье “Новое уравнение релятивистской квантовой механики” [1].
Таким образом, при правильном понимании выражения для квадрата импульса (1.4), вместо ошибочного уравнения Клейна-Гордона, получаем правильное уравнение М2.
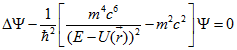 (1.7)
(1.7)
Замечания по поводу уравнения Дирака приведем позже, при сравнении решений с решениями уравнения М2.
Радиальное уравнение М2 для атома водорода
В работе [2] достаточно подробно было приведено решение угловой части уравнения М2. Поэтому сразу перейдем к решению радиального уравнения. Для нас важно, что квантовое число ![]() может принимать как целые так и полуцелые значения, включая значение
может принимать как целые так и полуцелые значения, включая значение ![]()
![]() Обоснование есть в работах [2] и [4]. Особый случай
Обоснование есть в работах [2] и [4]. Особый случай ![]() будем рассматривать отдельно.
будем рассматривать отдельно.
Запишем радиальное уравнение М2 для водородоподобных ионов с зарядом ядра ![]() :
:
.gif) (2.1)
(2.1)
Далее будем применять атомную систему единиц Хартри. ![]() .
.
Перепишем уравнение (1.1) в атомных единицах Хартри:
.gif) (2.2)
(2.2)
Для решения полученного уравнения, воспользуемся математическим интернет ресурсом WolframAlpha http://www.wolframalpha.com/
Решение уравнения (2.2) представляет из себя сумму двух линейно независимых частей. Обобщенных полиномов Лагерра и вырожденной гипергеометрической функции второго рода.
Воспользуемся вторым линейно-независимым решением. Который имеет вид:
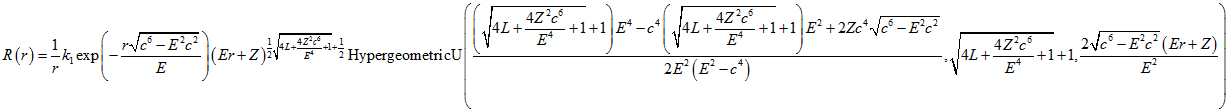
где ![]() вырожденная гипергеометрическая функция второго рода,
вырожденная гипергеометрическая функция второго рода, ![]() константа интегрирования.
константа интегрирования. ![]() где
где ![]() орбитальное квантовое число.
орбитальное квантовое число.
Как известно, первый параметр вырожденной гипергеометрической функции является радиальным квантовым числом со знаком минус ![]() .
.
Из этих соображений, получаем уравнение для определения энергии основного состояния и возбужденных состояний водородоподобных ионов в следующем виде:
.gif) (2.3)
(2.3)
Сначала найдем решения уравнения М2 для обычных водородных состояний. Решая уравнение (2.3) с параметрами ![]() и
и ![]() получим формулу энергий основного состояния водородоподобных ионов в атомных единицах Хартри в следующем виде:
получим формулу энергий основного состояния водородоподобных ионов в атомных единицах Хартри в следующем виде: ![]() (2.4) Полученная энергия включает в себя энергию покоя электрона
(2.4) Полученная энергия включает в себя энергию покоя электрона ![]() . Учитывая это окончательно запишем формулу энергии в электрон-вольтах.
. Учитывая это окончательно запишем формулу энергии в электрон-вольтах.
![]() эВ (2.5) Полученная формула энергии основного состояния водородоподобного ряда, точно совпадает с соответствующей формулой Дирака.
эВ (2.5) Полученная формула энергии основного состояния водородоподобного ряда, точно совпадает с соответствующей формулой Дирака.
Определим энергии атома водорода для основного состояния ![]() и первого возбужденного состояния с орбитальным моментом
и первого возбужденного состояния с орбитальным моментом ![]() .
.
Подставляя значения ![]() в формулу (2.5) получим энергию основного состояния:
в формулу (2.5) получим энергию основного состояния:
![]() эВ
эВ
Решая уравнение (2.3) с параметрами ![]() получим энергию первого возбужденного состояния:
получим энергию первого возбужденного состояния:![]() эВ.
эВ.
На основании полученных энергий, построим графики нормированной радиальной плотности вероятности для основного состояния и первого возбужденного состояния Рис.1.
Из уравнения (2.3) можно получить достаточно компактную универсальную формулу для расчета энергий водородоподобного ряда, в основном и в возбужденных состояниях, для уравнения М2, при условий равенства радиального и орбитального квантовых чисел: ![]() .
.
.gif) (2.6)
(2.6)
Квантовое число ![]() принимает значения из ряда
принимает значения из ряда ![]() с шагом
с шагом ![]() . Имеются некоторые различия в интерпретации квантовых чисел уравнения Дирака и уравнения М2. На этом подробно останавливаться в рамках данной работы не будем. При значении квантового числа
. Имеются некоторые различия в интерпретации квантовых чисел уравнения Дирака и уравнения М2. На этом подробно останавливаться в рамках данной работы не будем. При значении квантового числа ![]() формула (2.6) переходит в формулу энергии основного состояния (2.4) как и следовало ожидать.
формула (2.6) переходит в формулу энергии основного состояния (2.4) как и следовало ожидать.
Будем пользоваться только положительными значениями энергий, хотя уравнение М2 дает симметричные решения. Решения по формуле (2.6) очень хорошо согласуются с экспериментальными значениями.
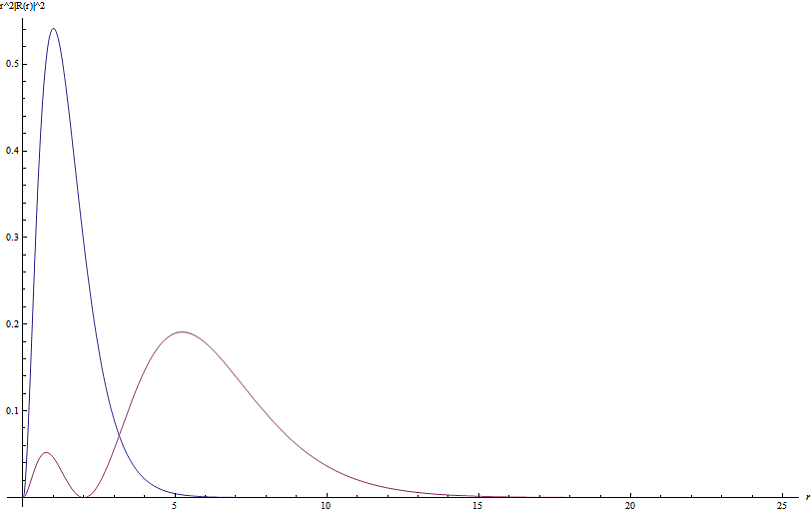
Рис.1. Нормированная радиальная плотность вероятности основного состояния и первого возбужденного состояния в атомных единицах Хартри.
Экзотические, сильно локализованные, компактные состояния водорода
Построим график зависимости энергии от радиального квантового числа для сферически симметричных состояний с орбитальным моментом ![]() согласно уравнению (2.3) Рис.2. На том же рисунке построим соответствующий график
согласно уравнению (2.3) Рис.2. На том же рисунке построим соответствующий график ![]() уравнения Дирака для сравнения. На графике точка 1 соответствует основному состоянию
уравнения Дирака для сравнения. На графике точка 1 соответствует основному состоянию ![]() . Точка 2 соответствует первому возбужденному состоянию
. Точка 2 соответствует первому возбужденному состоянию![]() .
.
Как можно заметить, в области энергий выше основного состояния, то есть выше точки 1, решения уравнений Дирака и М2 точно совпадают. Это область обычных возбужденных состояний. Однако в области энергий ниже основного состояния, поведение уравнений в корне отличаются. В этой области уравнение М2 имеет характерный изгиб. В результате такого поведения образуется точка 3. Это точка пересечения графика энергии с линией ![]() . Точка 3 это потенциально возможное решение с высокой локализацией электрона у ядра и с высокой энергией связи. Как видим подобные решения у уравнения Дирака отсутствуют. Поэтому, как было сказано, в области энергий ниже основного состояния, к решениям уравнения Дирака приведенным в различных работах [5],[6],[7],[8], надо относиться с осторожностью.
. Точка 3 это потенциально возможное решение с высокой локализацией электрона у ядра и с высокой энергией связи. Как видим подобные решения у уравнения Дирака отсутствуют. Поэтому, как было сказано, в области энергий ниже основного состояния, к решениям уравнения Дирака приведенным в различных работах [5],[6],[7],[8], надо относиться с осторожностью.
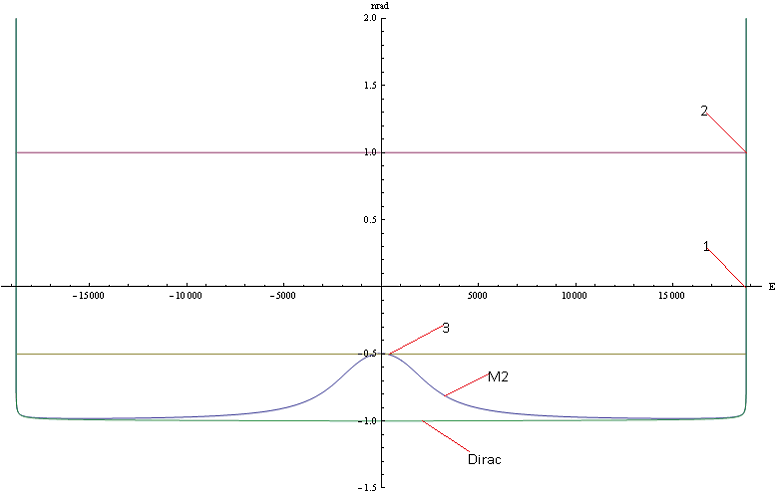
Рис.2. График зависимости энергии от радиального квантового числа ![]() при
при ![]() для уравнений Дирака и М2.
для уравнений Дирака и М2.
Предположение о существовании компактных локализованных состояний атома водорода, полагает наличие высокой энергии связи. Энергия связи должна быть выше чем принятого основного состояния. А это в свою очередь предполагает смещение радиального или орбитального квантового числа в сторону отрицательных значений ![]() или
или ![]() . Посмотрев на график зависимости энергии от квантового числа
. Посмотрев на график зависимости энергии от квантового числа ![]() Рис.2. можно понять, что таким значением является
Рис.2. можно понять, что таким значением является ![]() . Случай когда
. Случай когда ![]() особенный и будет рассмотрен отдельно. При этом единственно возможное отрицательное значение
особенный и будет рассмотрен отдельно. При этом единственно возможное отрицательное значение ![]() .
.
Определим энергию локализованного состояния 3 решая уравнение (2.3) с параметрами ![]() . Решение дает
. Решение дает .gif) (3.1) Подставляя в полученную формулу значение скорости света
(3.1) Подставляя в полученную формулу значение скорости света ![]() и значение заряда ядра
и значение заряда ядра ![]() получим энергию
получим энергию ![]() в атомных единицах Хартри. Полученная энергия включает в себя энергию покоя электрона
в атомных единицах Хартри. Полученная энергия включает в себя энергию покоя электрона ![]() .Учитывая это определим энергию связи и преобразуем в электрон-вольты
.Учитывая это определим энергию связи и преобразуем в электрон-вольты ![]() эВ.
эВ.
Построим график нормированной радиальной волновой функции для состояния 3. Рис. 3.
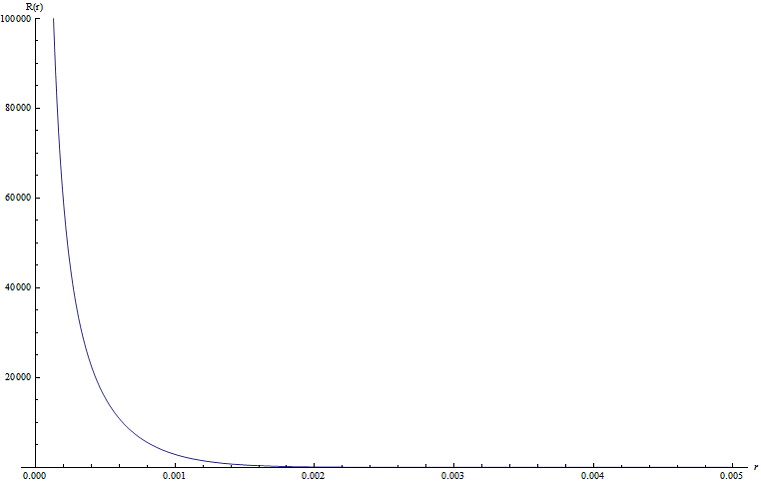
Рис.3. Нормированная радиальная волновая функция для состояния 3 при ![]() ,
, ![]() ,
,![]() эВ
эВ
Как видим волновая функция стремится к бесконечности при ![]() . Но такое поведение нельзя считать не физическим. Потому что, это следствие бесконечного роста в отрицательную сторону Кулоновского потенциала при
. Но такое поведение нельзя считать не физическим. Потому что, это следствие бесконечного роста в отрицательную сторону Кулоновского потенциала при ![]()
![]() . В реальности же, потенциал отличается от чисто Кулоновского при
. В реальности же, потенциал отличается от чисто Кулоновского при ![]() и является ограниченным снизу, так как ядро не является точечным а имеет размеры.
и является ограниченным снизу, так как ядро не является точечным а имеет размеры.
Построим график нормированной радиальной плотности вероятности для состояния 3. Рис. 4.
Таким образом, мы показали возможность существования у атома водорода сильно локализованных, компактных состояний с высокой энергией связи.
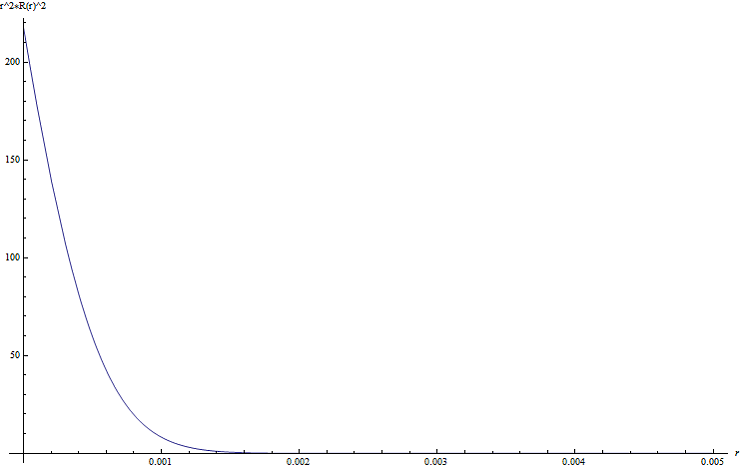
Рис.4. Нормированная радиальная плотность вероятности состояния 3
Манипулируя значениями квантовых чисел ![]() и
и ![]() в допустимых пределах, можно получить семейство таких решений. Покажем это в виде семейства графиков Рис.5. А затем приведем таблицу соответствующих значений энергий и квантовых чисел.
в допустимых пределах, можно получить семейство таких решений. Покажем это в виде семейства графиков Рис.5. А затем приведем таблицу соответствующих значений энергий и квантовых чисел.
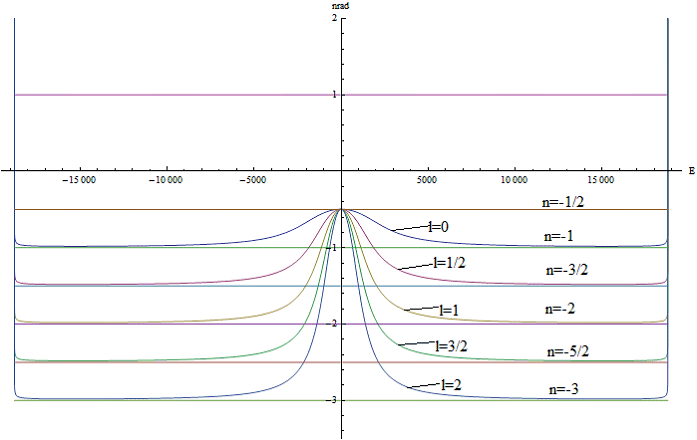
Рис.5 Семейство графиков зависимости энергии от радиального квантового числа ![]() при различных значениях квантового числа
при различных значениях квантового числа ![]()
|
Энергии связи компактного атома водорода в зависимости от квантовых чисел эВ
|
||||||||||
|
ln
|
-1/2
|
-1
|
-3/2
|
-2
|
-5/2
|
-3
|
-7/2
|
-4
|
-9/2
|
-5
|
|
0
|
- |
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
1/2
|
- |
- |
-
|
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
1
|
- |
- |
- |
-
|
-
|
-
|
-
|
-
|
-
|
-
|
|
3/2
|
- |
- |
- |
- |
-
|
-
|
-
|
-
|
-
|
-
|
|
2
|
- |
- |
- |
- |
- |
-
|
-
|
-
|
-
|
-
|
|
5/2
|
- |
- |
- |
- |
- |
- |
-
|
-
|
-
|
-
|
|
3
|
- |
- |
- |
- |
- |
- |
-
|
-
|
-
|
-
|
|
7/2
|
- |
- |
- |
- |
- |
- |
-
|
-
|
-
|
-
|
|
4
|
- |
- |
- |
- |
- |
- |
-
|
-
|
-
|
-
|
|
9/2
|
- |
- |
- |
- |
- |
- |
-
|
-
|
-
|
-
|
|
5
|
- |
- |
- |
- |
- |
- |
-
|
-
|
-
|
-
|
Компактный атом водорода и аннигиляционный пик
В различных природных явлениях, в излучении солнечной короны, в космических излучениях, при исследовании грозовых облаков, часто наблюдаются гамма фотоны с энергией ![]() кэВ. Такое излучение обычно объясняется аннигиляцией электрон-позитронной пары. Но во многих случаях, объяснить наличие антивещества в наблюдаемой зоне, просто невозможно.
кэВ. Такое излучение обычно объясняется аннигиляцией электрон-позитронной пары. Но во многих случаях, объяснить наличие антивещества в наблюдаемой зоне, просто невозможно.
Исследователь J.Va’vra [5] выдвигает гипотезу о том, что излучение ![]() кэВ может быть следствием захвата электрона протоном на низкую орбиту, в процессе образования компактного атома водорода.
кэВ может быть следствием захвата электрона протоном на низкую орбиту, в процессе образования компактного атома водорода.
Мы сейчас проверим эту гипотезу.
Излучение с энергией ![]() означает, что вся энергия электрона излучена и следовательно в уравнении надо подставить значение энергии
означает, что вся энергия электрона излучена и следовательно в уравнении надо подставить значение энергии ![]() . Запишем уравнение М2 с энергией
. Запишем уравнение М2 с энергией ![]()
.gif) (4.1) В работе [2] достаточно подробно было приведено решение угловой части уравнения М2. Поэтому сразу перейдем к решению радиального уравнения. Запишем радиальное уравнение М2 в атомных единицах Хартри с учетом
(4.1) В работе [2] достаточно подробно было приведено решение угловой части уравнения М2. Поэтому сразу перейдем к решению радиального уравнения. Запишем радиальное уравнение М2 в атомных единицах Хартри с учетом ![]() ,
, ![]() .
.
.gif) (4.2) Для решения полученного уравнения, воспользуемся математическим интернет ресурсом WolframAlpha http://www.wolframalpha.com/
(4.2) Для решения полученного уравнения, воспользуемся математическим интернет ресурсом WolframAlpha http://www.wolframalpha.com/
Решение имеет вид:
.gif) (4.3)
(4.3)
То есть является суммой двух линейно независимых частей. Вырожденной гипергеометрической функции второго рода и обобщенных полиномов Лагерра.
Воспользуемся первым линейно независимым решением.
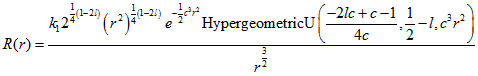 (4.4)
(4.4)
Где ![]() вырожденная гипергеометрическая функция второго рода и
вырожденная гипергеометрическая функция второго рода и ![]() константа интегрирования.
константа интегрирования.
Поскольку мы рассматриваем случай когда вся энергия электрона излучена, то естественно энергию состояния получим ![]() в единицах Хартри. Преобразуем в электрон-вольты
в единицах Хартри. Преобразуем в электрон-вольты ![]() эВ. Теперь пришло время рассмотрения особого случая когда
эВ. Теперь пришло время рассмотрения особого случая когда ![]() . Подставим это значение в уравнение (4.4) и определим константу интегрирования
. Подставим это значение в уравнение (4.4) и определим константу интегрирования ![]() из условия нормировки
из условия нормировки ![]() (4.5).
(4.5). ![]() Построим график нормированной радиальной волновой функции (4.4) при
Построим график нормированной радиальной волновой функции (4.4) при ![]() Рис. 6.
Рис. 6.
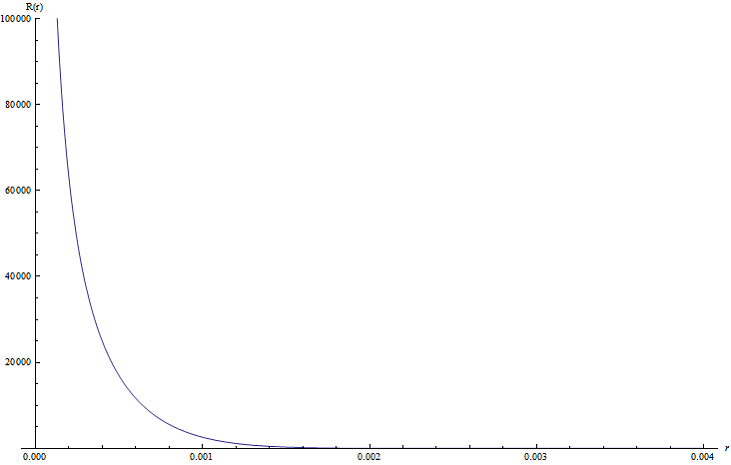
Рис. 6 График радиальной волновой функции (4.4) при ![]()
![]() эВ
эВ
Построим график нормированной радиальной плотности вероятности при ![]() Рис. 7.
Рис. 7.
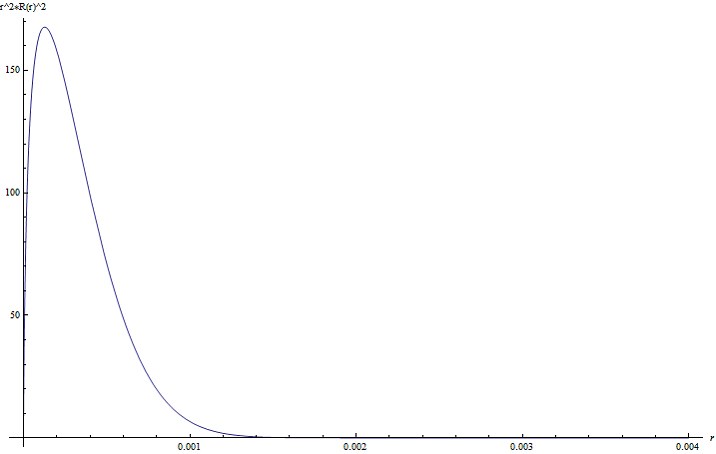
Рис. 7 Радиальная плотность вероятности при ![]() и
и ![]() эВ
эВ
Определим орбитальный радиус, то есть расстояние от начала координат до точки максимума плотности вероятности. ![]() в атомных единицах. Умножив полученное значение на радиус Бора
в атомных единицах. Умножив полученное значение на радиус Бора ![]() м получим
м получим ![]() м.
м.
Таким образом, путем решения уравнения М2, была доказана возможность существования, неизвестного до настоящего времени состояния, для атома водорода со следующими параметрами: Значение квантового числа ![]() . Значение энергии состояния
. Значение энергии состояния ![]() эВ. Значение орбитального радиуса
эВ. Значение орбитального радиуса ![]() м. При образовании данного состояния выделяется энергия
м. При образовании данного состояния выделяется энергия![]() кэВ, что подтверждает гипотезу J.Va’vra [5] о происхождении аннигиляционного пика связанного с образованием компактного атома водорода.
кэВ, что подтверждает гипотезу J.Va’vra [5] о происхождении аннигиляционного пика связанного с образованием компактного атома водорода.
Численное решение в цилиндрических координатах
Как и в предыдущий раз [2], при применении нестандартного значения квантового числа ![]() , желательно дополнительное подтверждение полученного аналитического решения. В предыдущей работе [2] этот вопрос подробно изложен. Поэтому сразу запишем уравнение М2 в цилиндрических координатах со значением энергии
, желательно дополнительное подтверждение полученного аналитического решения. В предыдущей работе [2] этот вопрос подробно изложен. Поэтому сразу запишем уравнение М2 в цилиндрических координатах со значением энергии ![]() , и со значением квантового числа
, и со значением квантового числа ![]() . Это означает, что энергия связи равна
. Это означает, что энергия связи равна ![]() эВ. Для водорода
эВ. Для водорода ![]() .
.
.gif) (5.1)
(5.1)
Для решения уравнения (5.1) будем пользоваться пакетом программ для численного решения систем дифференциальных уравнений FlexPDE http://www.pdesolutions.com/
В результате численного решения получены следующие значения параметров водорода в состоянии ![]() . Энергия связи
. Энергия связи ![]() эВ, орбитальный радиус
эВ, орбитальный радиус ![]() м.
м.
Что достаточно хорошо согласуется с данными аналитического решения.
Численное решение показало:1. Уравнение для состояния водорода с энергией связи ![]() эВ имеет достаточно высокую сходимость.
эВ имеет достаточно высокую сходимость.
2. Беспокойства по поводу сингулярного поведения угловой части волновой функции беспочвенны.
3. Следовательно имеются достаточно оснований для целесообразности экспериментального поиска водорода в состоянии с ![]() эВ и
эВ и ![]() м.Ниже приведем результаты решения в виде двумерных и трехмерных графиков радиальной плотности вероятности.
м.Ниже приведем результаты решения в виде двумерных и трехмерных графиков радиальной плотности вероятности.

Рис.8 Двумерный график радиальной плотности вероятности
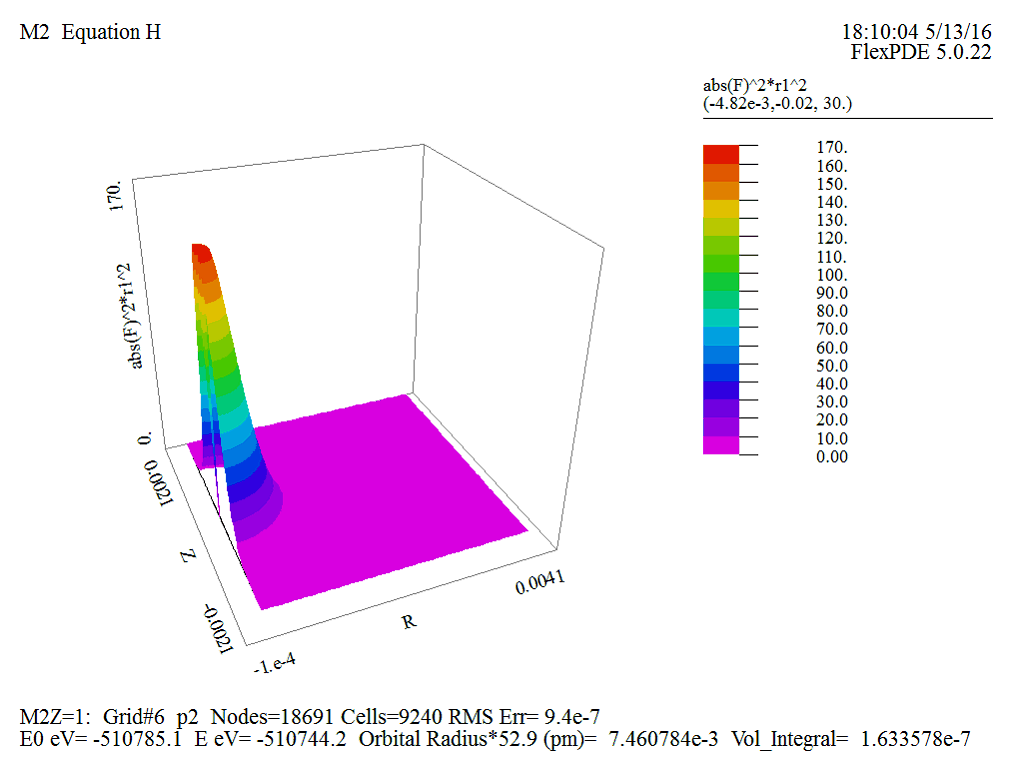
Рис.9 Трехмерный график радиальной плотности вероятности
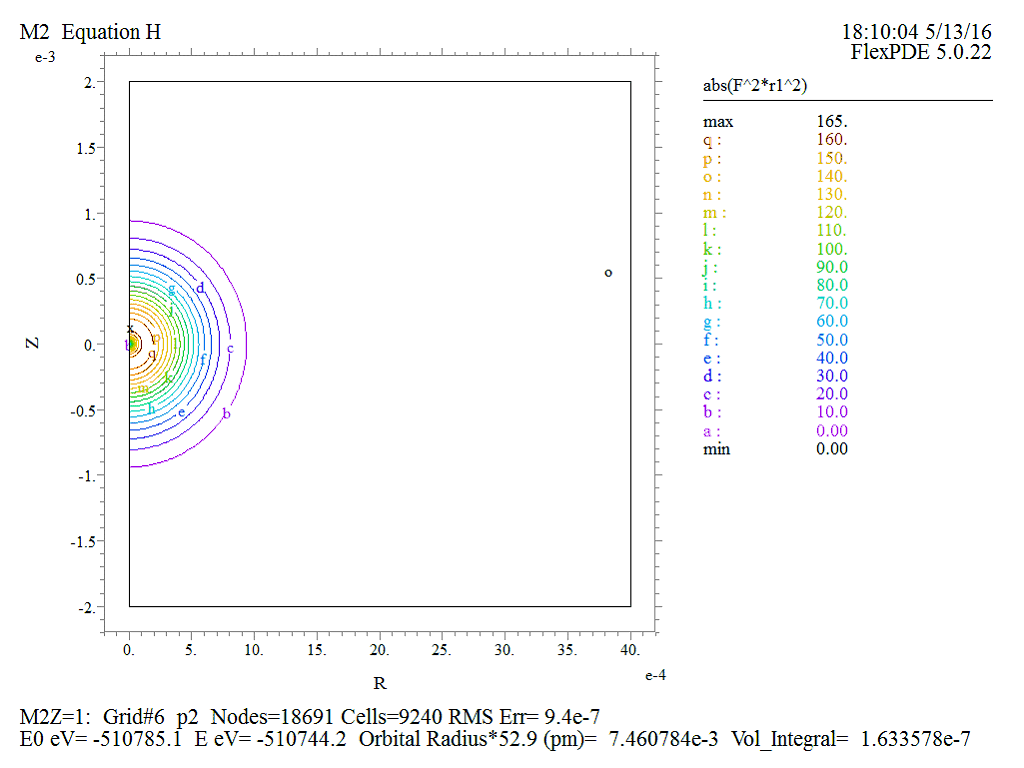
Рис.10 Проекция трехмерной радиальной плотности вероятности
Результаты и обсуждения
Найдена и устранена ошибка в уравнении Клейна-Гордона. В результате, подтверждена правильность уравнения М2. Следовательно, тему о многолетних спорах о противоречии СТО и квантовой механики, можно считать исчерпанной.
Применение уравнения М2 к атому водорода, выявило дополнительные тонкости в поведении электрона. Было получено семейство сильно локализованных состояний с высокой энергией связи. Получены значения энергий в зависимости от квантовых чисел. Во многих работах [5],[6],[7],[8], приведены подобные решения уравнения Дирака. Однако, во втором разделе было показано, что уравнение Дирака не имеет подобного поведения. И без дополнительной манипуляции с Кулоновским потенциалом, подобных решений не получится.
Далее аналитическим и численным решением уравнения М2, была доказана гипотеза J.Va’vra [5] о происхождении аннигиляционного пика связанного с образованием компактного атома водорода. Были получены параметры этого состояния: энергия связи ![]() эВ и орбитальный радиус
эВ и орбитальный радиус ![]() м.
м.
Думаем представлено достаточно теоретических оснований, для организации экспериментального поиска описанных состояний атома водорода.
Библиографический список
- Дангян А.Э. “Новое уравнение релятивистской квантовой механики”
- Дангян А.Э. “Атом Водорода Экзотические состояния. Часть первая”
- Дангян А.Э. “Позитроний”
- Дангян А.Э. “Волновая функция электрона”
- J. Va’vra, “A new way to explain the 511 keV signal from the center of the Galaxy and some dark matter experiments,” Astronomy & Astrophysics http://arxiv.org/pdf/1304.0833v3.pdf
- Arguments for the Anomalous Solutions of the Dirac Equations Jean-Luc Paillet, Andrew Meulenberg http://vixra.org/pdf/1506.0177v1.pdf
- Jan Naudts. On the hydrino state of the relativistic hydrogen atom. arXiv:physics/0507193v2
- Electron Deep Orbits of the Hydrogen Atom http://www.iscmns.org/work11/12%20Paillet-EDOH-Full1.pdf
- Курчатов И.В. “О возможности создания термоядерных реакций в газовом разряде”
- ELECTRON TRANSITIONS ON DEEP DIRAC LEVELS I JAROMIR A. MALY Applied Science Consultants 5819 Ettersberg Drive, San Jose, California 95123, JAROSLAV VAVRA Applied Science Consultants 67 Pine Lane, Los Altos, California 94022
