1. Introduction
In article [1] presents an overview of the state of immersion and convective heat transfer problems lithospheric plate in the subduction zone. In spite of a great number of publications dealing with a study of the natural mantle convection, the questions concerning the character, structure and the primary reason for occurrence of the convection remain still open. In fact, the influence of convection on the geometry of plates and, also, differences in the character of convection caused by using the Newtonian and non-Newtonian models of Earth’s mantle, has not been studied yet.
Undoubtedly, solution of these questions will entail great difficulties as at the stage of setting the problems so at the stage of their numerical solution. The above difficulties are caused by non-linearity of the problem, that is, the temperature and pressure dependence, practically, of all parameters of the mantle, lack of information on a lot of rheological parameters, restriction to the stability of the numerical solution due to prevalence of viscosity members over the inertial ones in the Navier-Stokes equations.
The main shortcoming of the above mathematical models is the fact that phases transitions at 670 km depth causing jumps in viscosity and density of the mantle substance which, in the opinion of some researchers, may lead to localization of the convection in the upper mantle, are not taken into account.
2. Formulation of the Problem
The paper considers a 2-D model of the continuous convection of the lithospheric plate close to oceanic trench with regard for the heat of the phase transition. The subduction zone is considered, where lithospheric plate collides with continental, and then on a trough, which axis is located under an angle to the land surface, is immersed in mantle. The depth of immersing of lithospheric plate in mantle is determined as a result of the task decision. Constructing the mathematical model, the following assumptions have been adopted [1]: the lithospheric plate and the underlying mantle are considered as the non-compressible Newtonian liquid with a very high viscosity. The temperature at a boundary between the mantle and the plate is constant and equals to the temperature of solid state Ts. The thermal conductivity , the viscosity of the substance and the heat flux qv are determined with account of their temperature dependence:
1. 
Index 1 denotes the lithosphere parameters, 2 – the mantle parameters. The dependence of the density p on the temperature of the medium is assumed to be
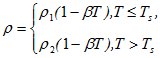
2. Border between lithosphere and mantle is isotherm of solid phase with value of temperature Ts.
3. The relative quantity of the solid phase (characterizing melting and crystallization of the substance) contained in the mantle or lithosphere is determined depending on the state of the substance (a solid state with a temperature TS or a liquid state with a temperature TL). The relative quantity of the solid phase , depending of temperature, approximates by cubic spline [1]:
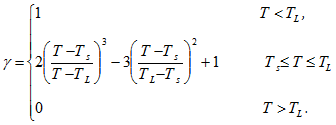
At < 0.95 it is assumed that the substance is in the melted (liquid) state, while at > 0.95 – in the solid state. A set of parameters for the lithosphere and the mantle used for the calculations are listed in the Table.
Following the hypothesis propounded in 1960 by H. Hess, the lithospheric plate motions are going on in a rectilinear manner starting from the areas of formation of the plates up to the zones of under thrusting, which allows us to solve the problem in a plane vertical layer. It results from systematic investigations of the island arc and continental margin zones that the depth of subsidence of the under thrusting plate does not exceed 700 km. Therefore, the extent of the area calculated along the Y-axis is assumed to be 1000 km. According to the results obtained, the extent of the calculated area along the X-axis is assumed to be 3000 km.
| Physical properties |
Lithosphere |
Mantle |
||||
| Viscosity m (Pa s) |
1022 |
1020 |
||||
| Thermal conductivity l (Wt/mK) Density r (kg/m3) Heat flux qv (Wt/m3) Specific heat capacity Cp (J/kgK) Volumetric expansion coefficient b (1/K) Heat of melting LF (J/kg) |
3 3000 5×10-6 1200 3×10-7 4×105 |
5 3300 10-9 1200 3×10-7 4×105 |
||||
3. Mathematical Model
Fig. 1 shows physical setting of a problem [1]. The horizontal oceanic plate moves towards the continental plate with a constant velocity U0, and subsides in the asthenosphere in the trench zone at an angle to the land surface with the same velocity. In turn, the continental plate moves towards the oceanic plate with a velocity Uk. Most often the lithospheric plates are subsiding in the subduction zones at an angle of 45°, though in some sectors of the island arcs the angles of subsidence from 30° to 90° have been marked. Here Uk - velocity of a continental plate, U0 - velocity of oceanic (lithospheric) plate; index 1 – lithosphere parameters, 2 – mantle parameters; – angle of immersing of oceanic plate; Г1, Г2, Г3 - right, lower and left border of a trench, on which the plate is immersed, accordingly.
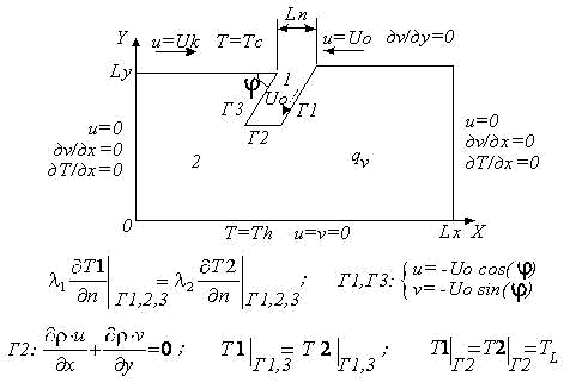
Fig. 1. Physical formulation of the problem
Location of trough, on which the plate is immersed, is considered equal Lx /2. The lower border Г2, up to which the velocity of immersing of a plate is known, is determined on the interval of temperature melting. At achievement of melting temperature (liquid) TL the lithospheric plate melts and depth of its immersing in mantle is determined.
The mathematical statement of a task describing convection in subduction zone includes the equations of movement of an incompressible liquid in the Boussinesq approximation, continuity and energy with account internal heat sources. The governing dimensionless equations can be written as [1]:
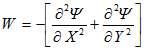 ,
,Where
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
. ![]() ,
, ![]() ,
, ![]() ,
, ![]() Stefan, Reynolds, Grashof and Peclet numbers.
Stefan, Reynolds, Grashof and Peclet numbers.
.gif)
.gif) .
.
.gif) .
.
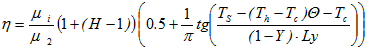 , H = [0;1] the dimensionless mantle depth.
, H = [0;1] the dimensionless mantle depth.
Boundary conditions:
![]() = 0 at Y = 1;
= 0 at Y = 1; ![]() = 1 at Y = 0;
= 1 at Y = 0; ![]() at X = 0 and X = Lx/Ly.
at X = 0 and X = Lx/Ly.
![]()
![]() , (k = 1,2,3) at border Г1, Г2, Г3 (fig. 1).
, (k = 1,2,3) at border Г1, Г2, Г3 (fig. 1).
![]() at border Г1, Г3;
at border Г1, Г3; ![]() at border Г2.
at border Г2.
![]() at X = [0; (Lx/2Ly - Lp/2Ly)]; Y = 1.
at X = [0; (Lx/2Ly - Lp/2Ly)]; Y = 1.
![]() at X = [(Lx/2Ly - Lp/2Ly); Lx/Ly]; Y = 1.
at X = [(Lx/2Ly - Lp/2Ly); Lx/Ly]; Y = 1.
![]() ,
, ![]() at X = [0; Lx/Ly];
at X = [0; Lx/Ly]; ![]() at
at![]() ;
; ![]() at Y = 0.
at Y = 0.
.gif) at
at ![]() (fig. 1).
(fig. 1).
![]() on Г1, Г3 (fig. 1) and inside a trench.
on Г1, Г3 (fig. 1) and inside a trench.
For intensity of a vortex W the boundary conditions were calculated with the use of boundary conditions for stream function. In accounts the non-uniform grid with a condensation in trench region and at the upper boundary of the area (Y = 1) was applied.
Dimensionless local Nusselt numbers on top (Y=1) and bottom (Y=0) to border of calculated area were determined by the expression ![]() (the derivative was calculated on three points with the second order of approximation).
(the derivative was calculated on three points with the second order of approximation).
The calculations were performed on a nonuniform grid with concentration nodes in the chute region, day surface and vertical boundaries of the computational domain (fig. 2).
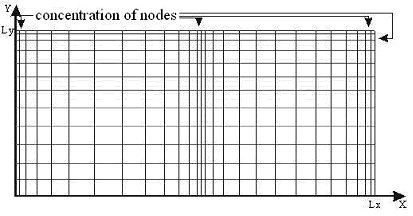
Fig. 2. The computational grid
Библиографический список
- Solovjov, S.V. Modeling immersing of lithosphere plate in mantle. Материали за 9–а международна научна практична конференция, «Новината за напреднали наука», – 2013. Том 53. Математика. София. «Бял ГРАД-БГ» ООД. – С. 43-48.
