Методы математической статистики играют огромную роль в естественных науках. В частности, регрессионный анализ позволяет установить качественную и количественную зависимость одной переменной от другой, то есть дать представление о виде зависимости и найти уравнение этой зависимости. Вопросу применения регрессионного анализа в физике посвящено немало научной литературы и диссертаций, среди которых можно выделить [1,2].
Рассмотрим вопрос о выявлении зависимости между средней по диску Солнца монохроматической яркости поверхности Солнца F_λ и длиной волны λ для трёх групп диапазонов: ультрафиолетового (УФ), видимого и инфракрасного (ИК). В качестве исходных данных для анализа используется таблица значений средней монохроматической яркостью поверхности Солнца F_λ и длиной волны λ [3, с 604].
Проведём регрессионный анализ средствами системы STATISTICA. На рисунке 1 «Результаты регрессии для УФ диапазона» приведены результаты регрессионного анализа, полученные в системе STATISTICA для первой группы данных (в УФ диапазоне). В качестве зависимых переменных выступает монохроматическая яркость поверхности Солнца F_λ. 

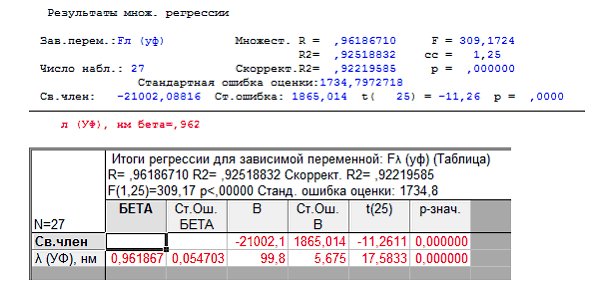
Разберёмся в полученных результатах. Обратим внимание на коэффициент детерминации R² = 0,92 . Так как данное значение близко к 1, то можно судить о значимости полученной модели. Об отвержении гипотезы об отсутствии линейной связи между исследуемыми признаками позволяет судить F-статистика Фишера. Значение F-статистики равняется 309,17 при p<0,0000. Таким образом, можно утверждать, что между средней монохроматической яркостью поверхности Солнца и длиной волны в УФ диапазоне существует ярко выраженная линейная зависимость. Значение всех полученных коэффициентов являются значимыми.По полученным данным составим уравнение регрессии в виде y=ax + b . Свободный член b = -21002,08816, коэффизиент a=99,8. Значит, искомое уравнение линейной зависимости имеет вид:
F_λ (УФ) = 99,8 • λ – 21002,1.
Графическое представление линейной зависимости показано на рисунке 2 «График линейной регрессии для УФ диапазона» (в виде сплошной линии). Пунктирной линией показан график экспериментальных значений (из исходной таблицы значений).

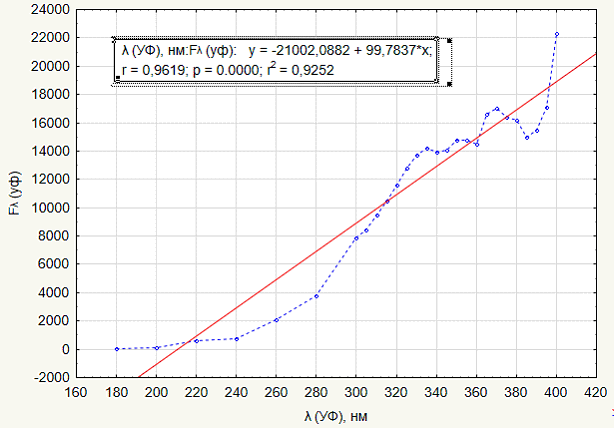
Рисунок 2. График линейной регрессии для УФ диапазона

Проведём регрессионный анализ для второй группы данных (в видимом диапазоне). На рисунке 3 «Результаты регрессии для видимого диапазона» показаны результаты данного анализа.

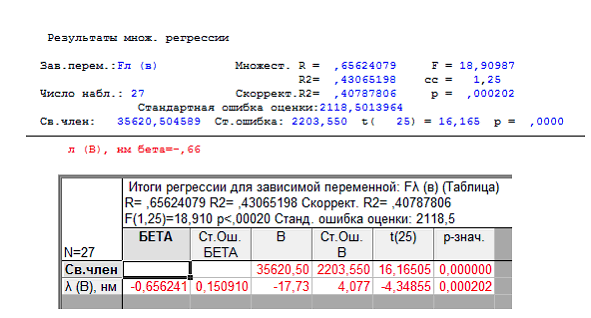
Рисунок 3. Результаты регрессии для видимого диапазона

Несмотря на низкое значение коэффициента R² = 0,41, следует отвержение гипотезы об отсутствии линейной связи между исследуемыми параметрами, так как F-статистики равняется 18,910 при p<0,002 (F >p). По свободному члену и коэффициенту при λ составляем уравнение линейной регрессии: 
F_λ (В) = -17,73 • λ + 35620,5.
Следует отметить, что линейная зависимость в данном случае выражена слабо.
Графическое представление линейной зависимости показано на рисунке 4 «График линейной регрессии для видимого диапазона».

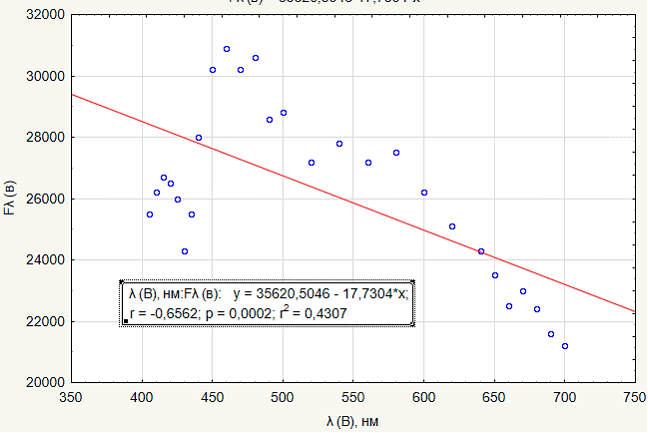
Рисунок 4. График линейной регрессии для видимого диапазона

Для третьей группы данных в инфракрасном диапазоне результаты регрессионного анализа показаны на рисунке 5 «Результаты регрессии для ИК диапазона»

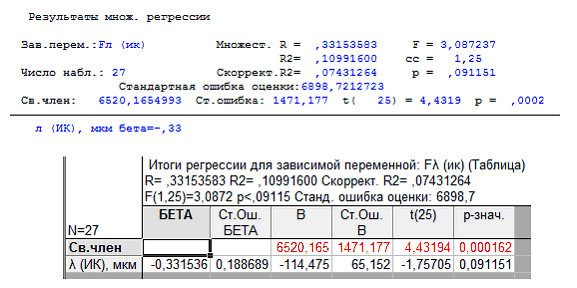
Рисунок 5. Результаты регрессии для ИК диапазона

Значение коэффициента R² = 0,07, что свиделельствует об отсутствие линейной зависимости между исследуемыми параметрами. В данном факте позволяет убедиться и графическое представление составленнной модели, изображенное на рисунке 6 «График линейной регрессии для ИК диапазона».

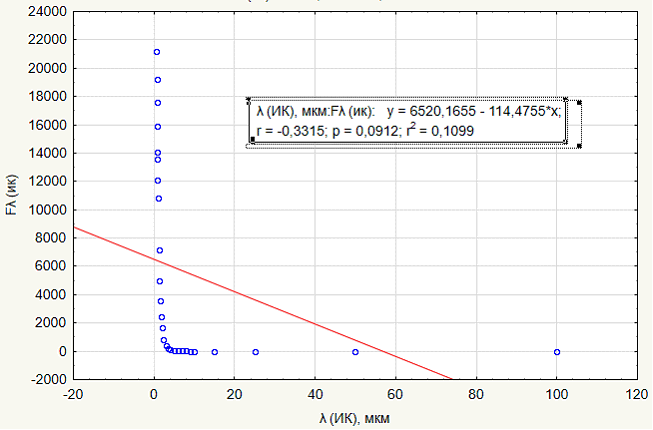
Рисунок 6. График линейной регрессии для ИК диапазона

В ходе регрессионного анализа получено отсутствие линейной зависимости между средней монохроматической яркостью поверхности Солнца и длиной волны в видимом и инфракрасном диапазонах, в то время как она ярко выражена в ультрафиолетовом диапазоне. Для убеждения в справедливости составленных моделей можно продемонстрировать график распределения частот в спектре излучения Солнца. Данный график представлен на рисунке 7 «График спектра Солнца». Он получается путём построения в одной системе координат данных для УФ, видимого и ИК диапазонов.

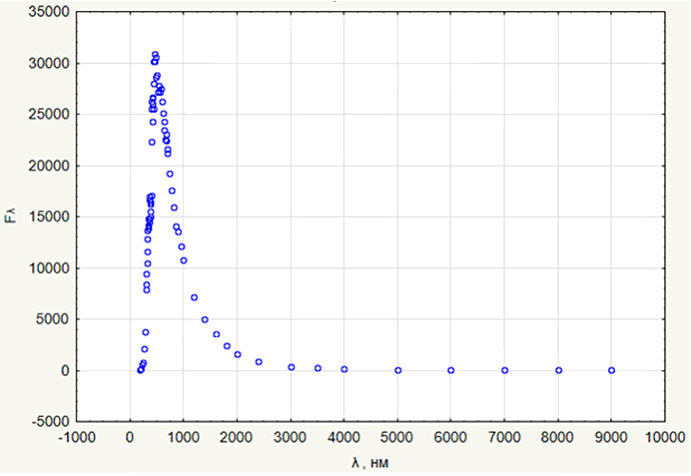
Рисунок 7. График спектра Солнца

Сравним поученный график с экспериментальным графиком, изображённом на рисунке 8 «Спектр излучения Солнца». Оба графика имеют идентичный вид.

Подбирая вид зависимости для модели, изображённой на рисунке 7, выяснено, что до полинома 6 степени не удаётся получить значимых коэффициентов уравнения регрессии, также значимые коэффициенты не получаются и при экспоненциальной и логарифмической зависимостях средней монохроматической яркости поверхности Солнца от длины волны.

1. Живописцев, Ф.А.,  Иванов, В.А. Регрессионный анализ в экспериментальной физике : М.: МГУ, 1995, Переплет: мягкий; 208 с.
2. Померанцев А.Л. Методы нелинейного регрессионного анализа для моделирования кинетики химических и физических процессов:  дис. … д-ра физ-мат. наук. Институт химической физики им Н.Н. Семенова Российской Академии Наук, Москва , 2003.
3. Куликовский П.Г. Справочник любителя астрономии.. Под ред. В. Г. Сурдина. Изд. 5-е, перераб. и полн. обновл. – М.: Эдиториал УРСС, 2002. – 688с.

Все статьи автора «Кульков Алексей Владимирович»