Введение.

Математическая безупречность любой теории ничего не говорит о ее истинности. Вот как об этом, применительно к геометрии, пишет Рейхенбах [1 с.22]:

«Если математик не связан использованием определенной системы аксиом и может применять аксиому не-а точно так же, как и аксиому а, тогда утверждение а не относится к математике, а математика есть не что иное, как наука об импликациях, то есть об отношениях типа «если …, то …». Следовательно, для геометрии как математической науки не существует проблемы истинности ее аксиом … Аксиомы не являются ни истинными, ни ложными, а лишь произвольными утверждениями».

Теория относительности построена чисто математически на двух постулатах (аксиомах или принципах), поэтому, если мы считаем эти постулаты верными, то обязаны считать верной и всю теорию. Однако, без дополнительных допущений признать постулаты теории относительности верными мы не можем, т.к. они взаимно противоречивы. Только допущение относительности времени устраняет их противоречивость [2 с.18]. Этот факт отмечал уже сам Эйнштейн [3 с.418]:

«Оказывается, что принцип постоянства скорости света и принцип относительности противоречат один другому только до тех пор, пока сохраняется постулат абсолютного времени, т.е. абсолютный смысл одновременности. Если же допускается относительность времени, то оба принципа оказываются совместимыми; в этом случае, исходя из этих двух принципов, получается теория, называемая «теорией относительности».

Таким образом, допущение относительности времени, так сказать, «склеивает» исходно несовместимые постулаты теории относительности. Общий подход к такой «склейке» заключается в следующем. Скорость (как и многие другие физические величины) не может быть измерена непосредственно, она может быть только вычислена как отношение длины пройденного отрезка пути к затраченному на это времени. Очевидно, что результат измерения времени, зависит от применяемой модели времени. Более того, и результат измерения длины зависит от применяемой модели времени, т.к. в движущейся системе отсчета она определяется посредством одновременного прикладывания измерительной линейки к началу и концу отрезка. Это означает, что при соответствующем «подборе» модели времени можно получить «нужную» зависимость скорости объекта от скорости системы отсчета, в которой анализируется его движение. Именно таким способом теория относительности добивается совместимости своих постулатов. Она декларирует такую модель времени, которая обеспечивает для одного и того же фотона одинаковую скорость сразу во всех инерциальных системах отсчета [4 с.454-455]. Следует отметить, что такой способ обеспечения совместимости постулатов теории относительности делает невозможной их прямую экспериментальную проверку, цитата [5 с.619]:

«На самом же деле возможность принять в каждой системе отсчета равенство скоростей света для противоположных направлений действительно зависит от свойств реального мира, в частности, от того факта, что в природе отсутствует мгновенная передача действий. Но принять это положение, в случае его допустимости, по мнению Пуанкаре, можно только в качестве соглашения, так как эксперимент в равной степени может быть согласован и с противоположным предположением о неравенстве этих величин».

Ввиду того, что исходная противоречивость аксиом теории относительности устранена за счет модификации модели времени, – полученную в результате новую модель, на наш взгляд, стоит исследовать на предмет отсутствия в ней внутренних противоречий. Лоренцево сокращение длины движущихся тел в теории относительности является прямым следствием релятивистской «относительности одновременности» [6 с.12; 7 с.71; 8 с.681], т.е. является прямым следствием используемой в этой теории модели времени. Лоренцево сокращение меняет геометрическую форму движущегося тела, поэтому форма тела в состоянии движения называется кинематической. Проанализируем далее совместимость кинематических форм тел при их сложном взаимосвязанном движении.

Противоречия совместимости кинематических форм тел при их сложном взаимосвязанном движении.

Рассмотрим тонкую жесткую симметричную цилиндрическую спираль, имеющую собственный шаг S₀. Спираль находится в трубе, которая имеет точно такие же форму и размеры (труба закручена как спираль, рис. 1). Трение между поверхностями спирали и трубы отсутствует. Труба и спираль неподвижны в некоторой инерциальной системе отсчета, ось x которой проходит по оси трубы (рис. 1).  Пусть труба остается неподвижной, а спираль постепенно приводится в движение, начинает «вкручиваться» в трубу (аналогично вкручиванию болта в гайку по резьбе). Труба не препятствует увеличению скорости точек спирали, т.к. скорость любого элементарного участка (далее Элемента) спирали  всегда направлена вдоль трубы. Ввиду того, что скорость любого Элемента спирали направлена вдоль него самого, – лоренцево сокращение каждого Элемента спирали приводит только к уменьшению его длины, оставляя параллельным стенкам трубы [3 с.74, 155; 9 с.302-303; 10 с.38, 182-183; 11 с.27; 7 с.72; 12 с.241-242]. То есть общая длина спирали уменьшается, но ее шаг остается неизменным. Поэтому спираль свободно движется в трубе. Пусть это будет утверждением №1.

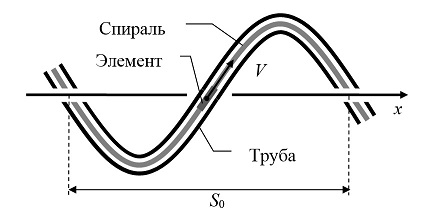Рис. 1. Жесткая спираль движется в неподвижной трубе.

Когда точки спирали достигают скорости V, ее ускорение прекращается. После окончания периода ускорения все точки спирали движутся вдоль оси x с одинаковой скоростью V_x. Перейдем теперь в систему отсчета, движущуюся со скоростью V_x. В этой системе отсчета спираль не движется поступательно, а только вращается вокруг своей оси. Труба же движется поступательно со скоростью – V_x. В этой системе отсчета, в результате лоренцева сокращения продольных размеров трубы, шаг «намотки» трубы будет уменьшен. Напротив, шаг спирали будет увеличен, т.к. угол наклона φ каждого Элемента спирали к ее оси, в результате лоренцева сокращения в направлении вектора скорости, – будет уменьшен (рис. 2) [9 с.135]. Это обусловлено тем, что размеры Элемента спирали уменьшаются только в направлении его скорости, а в перпендикулярном направлении остаются неизменными [3 с.74, 155; 9 с.302-303; 10 с.38, 182-183; 11 с.27; 7 с.72; 12 с.241-242].

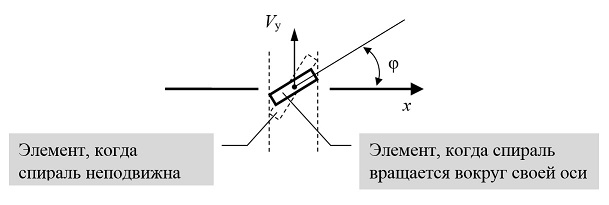Рис. 2. Элемент вращается вокруг оси спирали.

Таким образом, в этой системе отсчета шаг «намотки» трубы и спирали не могут совпадать. Следовательно, спираль не может свободно двигаться в трубе. Пусть это будет утверждением №2.

Утверждение №2 противоречит утверждению №1. Это означает, что релятивистское сокращение размеров движущихся тел логически противоречиво, и должно быть отброшено как ошибочное.

1. Рейхенбах Г. Философия пространства и времени, перевод с английского Ю.Б. Мочанова, общая редакция А.А. Логунова. – М.: Прогресс, 1985 (Philosophy of Space and Time by Hans Reichenbach. Translated by Maria Reichenbach and John Freund: witch introductory remarks by Rudolf Carnap, New York, 1958)
2. Терлецкий Я.П. Парадоксы теории относительности. – М.: НАУКА, 1966
3. Эйнштейн А. Собрание научных трудов. В 4 т. Т.I. Работы по теории относительности 1905-1920; под редакцией И.Е. Тамма, Я.А. Смородинского, Б.Г. Кузнецова. – М.: НАУКА, 1965
4. Грюнбаум А. Философские проблемы пространства и времени, перевод с английского Ю.Б. Молчанова, общая редакция Э.М. Чудинова. – М.: Прогресс, 1969 (Philosophical problems of space and time, Adolf Grünbaum; Andrew Mellon Professor of Philosophy UNIVERSITY OF PITTSBURGH; New York Alfred A. Knopf, 1963)
5. Тяпкин А.А. Выражение общих свойств физических процессов в пространственно-временной метрике специальной теории относительности // УФН. 1972. Т. 106, вып. 4. С. 617-659  (http://ufn.ru/ru/articles/1972/4/c/)
6. Гольденблат И.И. «Парадоксы времени» в релятивистской механике. – М.: НАУКА, 1972
7. Угаров В.А. Специальная теория относительности. – 2-е изд., испр. – М.: НАУКА, 1977
8. Сивухин Д.В. Общий курс физики. Учеб. пособие: для вузов. В 5 т. Т.IV. Оптика. – 3-е изд., стереот. – М.: ФИЗМАТЛИТ, 2005
9. Тоннела Мари-Антуанетт, Основы электромагнетизма и теории относительности, перевод с французского Г.А. Зайцева. – М: Издательство иностранной литературы, 1962 (Marie-Antoinette TONNELAT, Professeur a la Faculte des Sciences de Paris, LES PRINCIPES DE LA THEORIE ELECTROMAGNETIQUE ET DE LA RELATIVITE, MASSON ET CIE EDITEURS, PARIS, 1959)
10. Мёллер К. Теория относительности. – 2-е изд. – Пер. с англ. Под ред. проф. Д. Иваненко. – М.: Атомиздат, 1975 (THE THEORY OF RELATIVITY by C. Möller, second edition, Clarendon press, Oxford, 1972)
11. Ландау Л.Д., Лившиц Е.М. Теоретическая физика: Учеб. пособие. В 10 т. Т.II. Теория поля. – 7-е изд., испр. – М.: НАУКА, 1988
12. Борн М. Эйнштейновская теория относительности, перевод с английского Н.В. Мицкевича. – 2-е изд., испр. – М.: МИР, 1972 (EINSTEIN’S THEORY OF RELATIVITY by Max Born. Revised edition prepared with the collaboration of Gunter Leibfried and Walter Biem. Dover Publications Inc. New York 1962)

Все статьи автора «Бузмаков Игорь Витальевич»