Рассматривается система, состоящая из двух участников. Каждый из участников имеет возможность распределить имеющийся у него однородный бесконечно делимый ресурс между тремя проектами. Каждый из проектов характеризуется математическим ожиданием  и дисперсией  некоторого показателя эффективности. Проекты независимы друг от друга и их эффективности некоррелированы. Целью каждого участника является получение максимальной эффективности по сумме проектов. Дисперсия рассматривается в качестве негативного фактора. 
Предпочтения участников различаются: первый более осторожен и готов за снижение дисперсии расплачиваться существенным снижением эффективности, второй склонен к риску и готов мириться с высокой дисперсией при высоком математическом ожидании эффективности. Для учета индивидуальных предпочтений используется линейная свертка критериев. Такой подход позволяет однозначно выбрать оптимальное распределение ресурса по проектам для каждого из участников.
Задача оптимизации распределения ресурсов для каждого участника имеет вид:
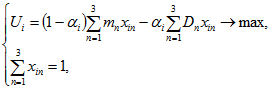 (1)
где  – полезность, получаемая i-ым участником,  – его степень неприятия риска,  – доля ресурсов, вкладываемая i-ым участником в n-ый проект. Решение задачи оптимизации (1) будем обозначать . 
После выбора оптимальных распределений участники могут рассмотреть целесообразность создания коалиции. Формирование коалиции целесообразно, если существует распределение ресурсов, являющееся доминирующим по Парето относительно суммарного распределения ресурсов обоими участниками без оптимизации в составе коалиции. В настоящей работе риск фиксировался на уровне суммарного распределения, а математическое ожидание эффективности максимизировалось. Задача оптимизации принимает вид:
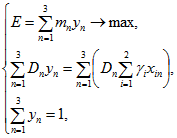 (2)
где  – доля средств i-го участника в средствах коалиции,  – доля средств коалиции, выделяемая на n-ый проект. Так как  заведомо удовлетворяет ограничениям задачи (2), то решение (2) гарантированно не хуже суммарного распределения без образования коалиции. Следовательно, не существует ситуации, когда образование коалиции было бы невыгодно для участников. Даже в самом неблагоприятном случае они получат при участии в коалиции ту же полезность, которую получили бы самостоятельно. Условия получения дополнительной полезности от объединения описаны в [1, с.71-89].
Эти выводы справедливы, когда участники знают точные значения всех  и . Часто некоторые (возможно, все) истинные значения  и  априори неизвестны, что вынуждает ориентироваться на их прогнозируемые значения. Очевидно, что ошибки прогнозирования могут повлиять на размер дополнительной полезности, получаемой участниками. При существенных ошибках участники могут получить полезность не только ниже прогнозируемой в составе коалиции, но и ниже получаемой самостоятельно. Возможные варианты перераспределения полезности в таких случаях приведены в [2].
На рис.1 представлен результат следующего численного эксперимента:
Исследуется размер δ превышения полезности от объединения в коалицию при ошибочном прогнозе над полезностью от объединения при точном прогнозе. В рассматриваемом примере , , , истинные значения , , , , , . Предполагается, что инвесторам неизвестны только истинные значения  и .
Была проведена серия численных экспериментов, в каждом из которых задавались прогнозные значения  и , для каждого инвестора решалась задача (1), затем решалась задача (2), после чего вычислялась величина δ. Рассматривались прогнозные значения  и . Шаг дискретизации по обеим переменным был выбран равным 0,01.
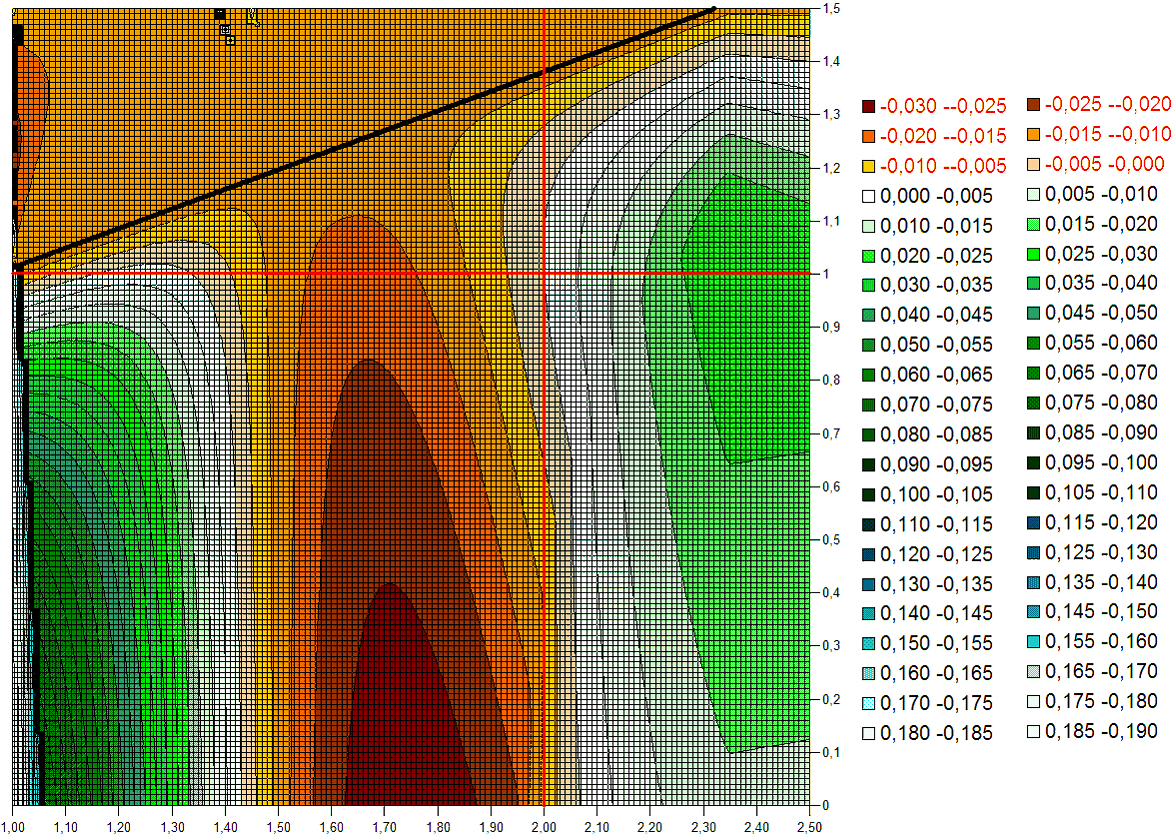
Для большей наглядности результаты этого же эксперимента представлены на диаграмме (рис.2) в виде линий уровня (красные линии – истинные значения  и ).

Рисунок 1. Превышение полезности от объединения в коалицию при ошибочном прогнозе над полезностью от объединения при точном прогнозе при различных прогнозах m2 и m3.

Рисунок 2. Линии уровня функции δ(m2,m3)

Поверхность  содержит несколько областей с существенно различающимися свойствами. Можно выделить следующие основные области (разделены черными линиями на рис.2):I. Область определяется неравенством . В этой области , то есть полученная дополнительная полезность оказалась немного ниже прогнозируемой. При этом объединение все равно осталось выгодным. Попадание в эту область, хотя и разочаровывает несбывшимися ожиданиями, но не является источником разрушительных явлений для коалиции.
II. Область резкого изменения δ. Резкое, практически скачкообразное изменение δ наблюдается при значениях . В данном эксперименте попадание в указанную область дает участникам неожиданно большое преимущество. 
III. Область гладкости функции . Изменения величины  существенны, однако не носят катастрофического характера. Возможность распада коалиции определяются в значительной мере погрешностью прогноза.В экспериментах с другими параметрами иногда также наблюдались подобные скачкообразные изменения, в том числе и приводящие к потерям полезности. Выявление характерных особенностей и предпосылок столь резкого изменения дополнительной полезности позволит проектировать механизмы формирования высокоэффективной коалиции.

1. Болдырева И.А., Бородач Ю.В., Головко В.Б., Малышенко В.А., Малышенко К.А., Саркисов В.Г., Финогенова Ю.Ю. Финансовый рынок и финансово-инвестиционная инфраструктура. Новосибирск, 2015.
2. Саркисов В.Г. Влияние ошибок прогноза на взаимодействие участников коалиции при управлении коллективным инвестиционным портфелем // Сборник материалов IX Всероссийской научной конференции «Математическое моделирование развивающейся экономики, экологии и технологий», ЭКОМОД-2016, – Киров: ВятГУ, 2016, стр.405-409.

Все статьи автора «Саркисов Виген Геннадьевич»