дальняя электропередача, установка продольной емкостной компенсации, степень компенсации, режимные характеристики, напряжение в линии, distant electricity transmission, installation of longitudinal capacitor compensation, extent of compensation, regime characteristics, tension in the line, jet power.
В настоящее время режимы работы электроэнергетической системы России характеризуются существенным изменением потоков мощности по дальним линиям электропередачи сверхвысокого напряжения. Продолжающийся рост нагрузки и проблемы, связанные с сооружением новых линий, требуют увеличения пропускной способности существующих линий электропередачи и управления их режимами в целях оптимального распределения потоков мощности между ними. Продольная емкостная компенсация индуктивного сопротивления воздушных линий электропередачи – одно из эффективных средств повышения пропускной способности, характеризуется следующими достоинствами:
Позволяет изменять пропускную способность в широком диапазоне при легко реализуемом строго заданном ее увеличении;
Обеспечивает развитие компенсирующего воздействия в процессе эксплуатации в соответствии с изменяющимися требованиями к устойчивости функционирования ЭЭС за счет расширения существующих и сооружения новых устройств продольной компенсации (УПК).
Продольную емкостную компенсацию можно выполнить двумя путями – сосредоточенная компенсация и распределенная. В первом случае УПК сооружается только в одной точке линии, во втором – в двух или более точках. В отечественной литературе рассматривалась как сосредоточенная компенсация [4-6], так и распределенная [3]. Установка УПК в нескольких точках линии позволяет снизить напряжение на выводах конденсаторных батарей (КБ) по сравнению с сосредоточенной компенсацией в одной точке линии. Также были определены оптимальные расстояния между УПК, при которых напряжение на выводах КБ оказывается меньше допустимых значений во всех режимах, что исключает необходимость включения шунтирующих реакторов на эти выводы, которые усложняют схему УПК и увеличивают стоимость всего устройства [3].
В ранних исследованиях анализировались режимные характеристики длинной линии с продольной компенсацией без промежуточных отборов мощности. Отсюда возникают новые задачи для исследования:
- анализ режимных характеристик линии с промежуточным отбором мощности при установке двух УПК;
- определение оптимальных расстояний между УПК с точки зрения пропускной способности и напряжения на выводах УПК при наличии промежуточного отбора мощности;
- распределение напряжения и реактивной мощности по линии в различных нормальных режимах работы.
Наибольшая мощность, которую по условию статической апериодической устойчивости можно передать по линии с установкой продольной емкостной компенсацией, определяется выражением:
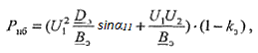
где U1, U2 - напряжения по концам линии; Bэ,Dэ – коэффициенты эквивалентного четырехполюсника, замещающего компенсированную линию; kз — коэффициент запаса по статической апериодической устойчивости.
Из уравнения (1.1) видно, что передаваемая по линии мощность будет достигать максимума при минимальном значении коэффициента Bэ. При этом следует учесть, что значение этого коэффициента будет определяться как взаимным расположением компенсирующих устройств, так и степенью компенсации индуктивного сопротивления линии. Расчеты следует производить с учетом этих факторов. При сосредоточенной емкостной компенсации оптимальное расположение УПК находится в средней точке линии [3], так как при таком расположении устройства коэффициент Bэ имеет минимальное значение.
Рассматривается линия с двумя установками продольной емкостной компенсации, одна из которых управляемая, другая – неуправляемая с неизменной степенью компенсации. Схема линии с двумя УПК и промежуточным отбором мощности представлена на рис. 1.1. В схеме не учитываются эквивалентные сопротивления передающей и приемной систем.

Рис. 1.1. Схема электропередачи.
Степень компенсации изменяется от 20 до 60%. Суммарная степень (коэффициент) компенсации kс определяется как
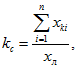 (1.2)
(1.2)где ![]() - суммарное сопротивление УПК, установленных на линии; хл -реактивное сопротивление линии, которое определяется как:
- суммарное сопротивление УПК, установленных на линии; хл -реактивное сопротивление линии, которое определяется как:
В рассматриваемом случае суммарное сопротивление УПК находится как
где xk1 - сопротивление регулируемой УПК; xk2 — сопротивление нерегулируемой УПК, ![]() .
.
Отсюда уравнение (1.2) может быть записано как
Из этого уравнения рассчитывается требуемое сопротивление управляемой УПК:
В математической модели линии значение коэффициента Bэ будет изменяться при перемещении двух УПК по линии, а также при изменении степени компенсации. Минимальному значению Bэ соответствует определенное (оптимальное) расстояние между УПК, которое предстоит найти, что является одной из задач данной работы.
Анализ проводился для одноцепных линий 500 кВ с проводами 3хАС-400/51 длиной от 300 до 1500 км с промежуточным отбором мощности. Длины крайних участков (l1=l4) и длины участков, прилегающих к точке отбора мощности (l2=l3), равны. Кроме того, участки l2 и l3 дают в сумме длину Lx, являющуюся оптимальным расстоянием между УПК.
Отсюда общая длина линии L равна
а расстояние между УПК
Последнее выражение позволяет найти расстояние между УПК при заданной общей длине линии и изменении расстояния между началом линии и первым УПК.
Для того, чтобы решить выше поставленную задачу, следует использовать метод эквивалентного четырехполюсника.
Схема линии приобретает вид:
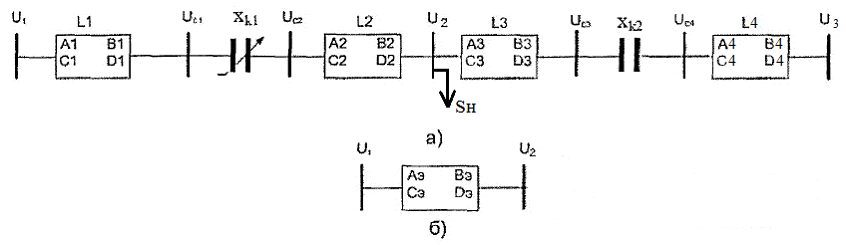
а – схема электропередачи, б – эквивалентный четырехполюсник.
Математическое описание такой линии представлено уравнением:
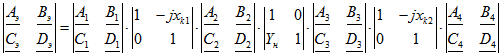 , (1.9)
, (1.9)где ![]() - комплексная проводимость нагрузки .
- комплексная проводимость нагрузки .
Оптимальное расположение УПК определяется диапазоном значений величины Lx, при которых величина Bэ будет иметь минимальные значения, в таком случае рассматриваемая линия будет обладать наибольшей пропускной способностью. Ниже, в табл. 1.1, приводятся результаты расчетов, выполненные в системе Mathcad для линии 500 кВ различной длины (300, 500, 750, 1000, 1500 км).
Диапазон изменения величины Lx лежит в пределах от 0 ÷ L км. Первое значение (Lx=0) соответствует сосредоточенной компенсации, при которой два УПК расположены в середине линии. Второе значение (Lx= L) соответствует расположению двух УПК по концам рассматриваемой линии.
Значения Bэ=f(Lх) рассчитаны для различных степеней компенсации от 0,2 до 0,6.
Следует отметить, что степень компенсации равная 0,2 соответствует работе только одной (неуправляемой) УПК. Вторая (управляемая) УПК в данном случае выведена из работы. При этом указанный выше диапазон изменения Lх соответствует перемещению неуправляемой УПК из середины линии в ее конец.
Оптимальное расположение двух УПК определяется диапазоном расстояния между ними, при котором значение коэффициента Bэ не превышает 0,25% от минимального.
Все расчеты выполнены для реальных линий, то есть с учетом активного сопротивления проводов. Алгоритм расчета и детальное описание полученных значений приведены в [1].
|
Линия, км
|
kс
|
Lх, км (Bэmin)
|
Lх опт, км
|
Bэmin
|
Bэmах
|
Delta,%
|
|
300
|
0,2
|
2
|
0-191
|
73,38
|
73,83
|
0,6
|
|
0,3
|
40
|
0-185
|
64,52
|
65,03
|
0,8
|
|
|
0,4
|
59
|
0-176
|
55,66
|
56,25
|
1,0
|
|
|
0,5
|
70
|
0-166
|
46,83
|
47,5
|
1,4
|
|
|
0,6
|
78
|
0-157
|
38,05
|
38,79
|
1,9
|
|
|
500
|
0,2
|
5
|
0-195
|
120,43
|
122,42
|
1,6
|
|
0,3
|
63
|
0-212
|
106,61
|
108,91
|
2,1
|
|
|
0,4
|
95
|
0-213
|
92,78
|
95,42
|
2,8
|
|
|
0,5
|
113
|
15-212
|
78,97
|
81,98
|
3,7
|
|
|
0,6
|
125
|
43-207
|
65,22
|
68,62
|
5,0
|
|
|
750
|
0,2
|
12,5
|
0-203
|
174,53
|
180,67
|
3,4
|
|
0,3
|
90
|
0-240
|
156,45
|
163,71
|
4,4
|
|
|
0,4
|
130
|
5-255
|
138,29
|
146,79
|
5,8
|
|
|
0,5
|
155
|
50-260
|
120,15
|
129,93
|
7,5
|
|
|
0,6
|
173
|
85-260
|
102,06
|
113,15
|
9,8
|
|
|
1000
|
0,2
|
20
|
0-213
|
220,41
|
233,23
|
5,5
|
|
0,3
|
107
|
0-263
|
200,7
|
216,33
|
7,2
|
|
|
0,4
|
153
|
23-283
|
180,87
|
199,49
|
9,3
|
|
|
0,5
|
183
|
293-733
|
161,01
|
182,71
|
11,9
|
|
|
0,6
|
203
|
106-300
|
141,19
|
166,01
|
15,0
|
|
|
1500
|
0,2
|
45
|
0-245
|
274,19
|
303,58
|
9,7
|
|
0,3
|
115
|
0-280
|
258,54
|
297,07
|
13,0
|
|
|
0,4
|
155
|
10-300
|
242,79
|
290,61
|
16,5
|
|
|
0,5
|
180
|
50-310
|
227
|
284,21
|
20,1
|
|
|
0,6
|
200
|
85-315
|
211,22
|
277,87
|
24,0
|
В задачу исследования также входит определение параметров режима электропередачи при расположении двух УПК на оптимальном расстоянии между ними, значения которого были определены.
К числу параметров режима, подлежащих определению, относятся:
- напряжения на выводах конденсаторных батарей;
- значения реактивных мощностей по концам всех участков линии;
- напряжение в средней точке линии.
При заданной начальной степени компенсации определяется значение хk1, затем определяются значения коэффициентов всех четырехполюсников, включенных в расчет, и находятся значения коэффициентов эквивалентного четырехполюсника, замещающего всю электропередачу. После этого при заданных значениях активной мощности начала линии, напряжений начала и конца линии находится угол фазового сдвига между напряжениями по концам линии (угол δ). Затем определяются реактивная мощность и ток ![]() начала линии.
начала линии.
Схема электропередачи приведена на рис. 1.2.

а)
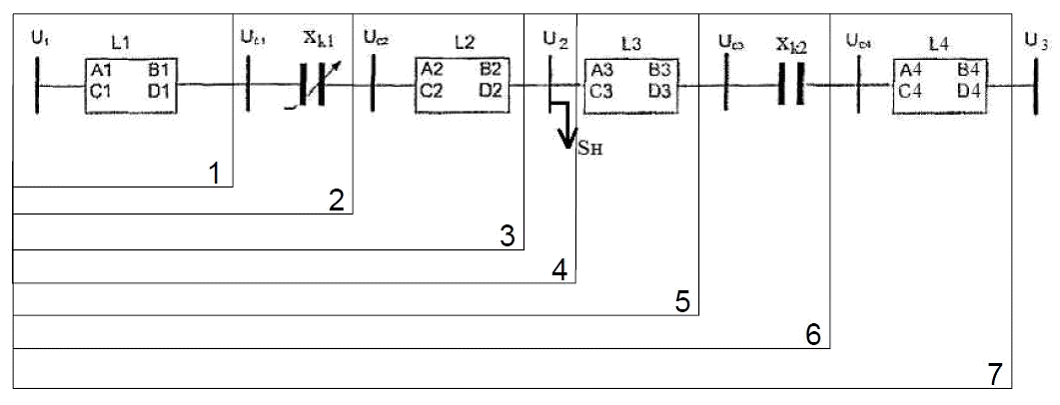
б)Рис. 1.2. Схема линии электропередачи (а), ее представление в виде эквивалентных четырехполюсников (б).
Наибольшая мощность, которую можно передать по компенсированной линии с учетом ограничения по статической апериодической устойчивости определяется как
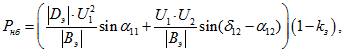 (1.10)
(1.10)где ![]() — нормируемый коэффициент запаса, равный 0,2, а Bэ соответствует минимальному коэффициенту эквивалентного четырехполюсника, в котором учеты обе установки продольной емкостной компенсации; коэффициент Bэ является функцией длины и степени компенсации.
— нормируемый коэффициент запаса, равный 0,2, а Bэ соответствует минимальному коэффициенту эквивалентного четырехполюсника, в котором учеты обе установки продольной емкостной компенсации; коэффициент Bэ является функцией длины и степени компенсации.
Наибольшие активные мощности, которые можно передать по компенсированной линии 500 кВ с проводами марки 3хАС-400/51 для различных длин линии, приведены в табл. 1.2.
|
kc / L,км
|
300
|
500
|
750
|
1000
|
1500
|
|
0
|
2400
|
1480
|
1050
|
861
|
751
|
|
0,2
|
3010
|
1840
|
1270
|
1010
|
826
|
|
0,3
|
3470
|
2100
|
1430
|
1120
|
882
|
|
0,4
|
4090
|
2460
|
1650
|
1260
|
948
|
|
0,5
|
4970
|
2950
|
1930
|
1440
|
1020
|
|
0,6
|
6320
|
3680
|
2330
|
1670
|
1110
|
Следует отметить еще одно обстоятельство: пропускная способность некомпенсированной линии длиной 300 км с учетом коэффициента запаса по статической апериодической устойчивости составляет порядка 2400 МВт, что превышает допустимую мощность по нагреву проводов (2055 МВт). Поэтому продольная емкостная компенсация, предназначенная для повышения пропускной способности для такой линии не нужна. Однако она может потребоваться при работе этой линии в сложной неоднородной сети для нормализации режима сети. В этом случае высокая степень компенсации очевидно не потребуется. Этот вопрос требует отдельного изучения.
Режимные характеристики такой линии, рассчитанные по приведенной выше методике, приведены в таблицах 1.3 и 1.4. Расчеты произведены при степени компенсации 0,2 и 0,3, так как задачей в работе ставится определение оптимальных условий работы УПК без установки шунтирующих реакторов, а не исследование способов нормализации режимов. Значение максимально возможной передаваемой мощности принято близким к допустимому по нагреву проводов – 2000 МВт.
Для протяженных линий свыше 1000 км определяющим является условие по апериодической устойчивости.
Далее приведены режимные характеристики линий 300-1500 км. Графики зависимости напряжения в промежуточных точках линий от расстояния между УПК и анализ табличных данных приведены в [1].
|
P, МВт
|
Uc1, кВ
|
Uc2, кВ
|
U2, кВ
|
Uc3, кВ
|
Uc4, кВ
|
|
kc = 0,2
|
|||||
|
0
|
503,45
|
503,45
|
503,43
|
503,45
|
502,45
|
|
430
|
503,5
|
503,5
|
503,49
|
50353
|
500,74
|
|
860
|
501,65
|
501,65
|
501,66
|
501,71
|
497,12
|
|
2000
|
486,38
|
486,38
|
486,48
|
486,63
|
477,07
|
|
kc = 0,3
|
|||||
|
0
|
503,17
|
503,52
|
503,17
|
503,49
|
503,33
|
|
430
|
503,81
|
503,2
|
503,08
|
503,65
|
501,55
|
|
860
|
502,97
|
501,33
|
501,45
|
502,43
|
498,3
|
|
2000
|
493,11
|
488,27
|
489,22
|
491,95
|
481,92
|
|
P,МВт
|
Q1, Мвар
|
Qk1, Мвар
|
Qxk1, Мвар
|
Qn2, Мвар
|
Qk2, Мвар
|
Qn3, Мвар
|
Qk3, Мвар
|
Qxk2, Мвар
|
Qn4, Мвар
|
Q3, Мвар
|
|
kc = 0,2
|
||||||||||
|
0
|
-105,6
|
30,4
|
0,0
|
30,4
|
31,3
|
-29,6
|
-28,7
|
1,7
|
-27,0
|
104,5
|
|
430
|
-123,1
|
-21,1
|
0,0
|
-21,1
|
-20,4
|
-81,4
|
-80,4
|
5,9
|
-74,6
|
47,2
|
|
860
|
-86,2
|
-84,9
|
0,0
|
-84,9
|
-84,9
|
-145,3
|
-145,0
|
36,6
|
-108,4
|
-63,9
|
|
2000
|
300,1
|
-319,4
|
0,0
|
-319,4
|
-323,6
|
-380,4
|
-383,9
|
258,3
|
-125,6
|
-642,1
|
|
kc = 0,3
|
||||||||||
|
0
|
-98,9
|
19,5
|
0,0
|
19,5
|
37,9
|
-22,9
|
-5,1
|
1,7
|
-3,5
|
111,1
|
|
430
|
-126,1
|
-37,3
|
6,6
|
-30,8
|
-16,9
|
-77,6
|
-61,2
|
5,7
|
-55,5
|
50,9
|
|
860
|
-105,4
|
-104,5
|
26,3
|
-78,2
|
-77,7
|
-138,1
|
-132,1
|
36,1
|
-96,0
|
-56,3
|
|
2000
|
193,3
|
-335,0
|
145,5
|
-189,4
|
-270,5
|
-327,3
|
-395,9
|
251,5
|
-144,2
|
-579,4
|
|
P, МВт
|
Uc1, кВ
|
Uc2, кВ
|
U2, кВ
|
Uc3, кВ
|
Uc4, кВ
|
|
kc = 0,3
|
|||||
|
0
|
512,04
|
512,36
|
511,87
|
512,24
|
512,74
|
|
430
|
512,51
|
511,2
|
511,1
|
511,97
|
509,17
|
|
860
|
508,79
|
505,65
|
506,03
|
507,7
|
501,4
|
|
2000
|
471,9
|
461,55
|
463,81
|
470,08
|
452,16
|
|
kc = 0,4
|
|||||
|
0
|
511,87
|
511,74
|
511,17
|
511,47
|
512,9
|
|
430
|
513,71
|
510,07
|
510,13
|
511,26
|
509,17
|
|
860
|
512,54
|
505,41
|
505,81
|
508,06
|
502,44
|
|
2000
|
492,21
|
475,41
|
474,99
|
482,12
|
466,61
|
|
kc = 0,5
|
|||||
|
0
|
512,06
|
510,95
|
510,48
|
510,77
|
512,56
|
|
860
|
517,19
|
504,43
|
505,02
|
507,75
|
502,14
|
|
2000
|
511,51
|
485,74
|
482,44
|
488,94
|
475,75
|
|
P, МВт
|
Q1, Мвар
|
Qk1, Мвар
|
Qxk1, Мвар
|
Qn2, Мвар
|
Qk2, Мвар
|
Qn3, Мвар
|
Qk3, Мвар
|
Qxk2, Мвар
|
Qn4, Мвар
|
Q3, Мвар
|
|
kc = 0,3
|
||||||||||
|
0
|
-190,2
|
11,05
|
0,01
|
11,06
|
41,13
|
-21,75
|
7,41
|
2,77
|
10,19
|
204,38
|
|
430
|
-202,7
|
-50,86
|
10,25
|
-40,61
|
-17,38
|
-80,07
|
-52,88
|
8,35
|
-44,53
|
138,52
|
|
860
|
-135,1
|
-129,2
|
41,27
|
-88,01
|
-85,88
|
-147,3
|
-136,4
|
55,75
|
-80,72
|
-6,02
|
|
2000
|
540,7
|
-439,7
|
252,5
|
-187,2
|
-329,6
|
-381,2
|
-502,7
|
441,05
|
-61,72
|
-877,8
|
|
kc = 0,4
|
||||||||||
|
0
|
-188,5
|
-2,32
|
0
|
-2,32
|
42,69
|
-20,02
|
23,61
|
2,82
|
26,43
|
206,0
|
|
430
|
-214,2
|
-74,15
|
20,75
|
-53,4
|
-18,81
|
-81,26
|
-40,61
|
8,28
|
-32,33
|
137,1
|
|
860
|
-170,7
|
-165,4
|
82,71
|
-82,75
|
-79,62
|
-141,0
|
-124,5
|
55,21
|
-69,32
|
0,75
|
|
2000
|
330,31
|
-516,2
|
477,14
|
-39,13
|
-237,1
|
-291,1
|
-457,1
|
411,31
|
-45,74
|
-737,4
|
|
kc = 0,5
|
||||||||||
|
0
|
-190,5
|
-12,98
|
0,03
|
-12,96
|
40,6
|
-21,95
|
29,97
|
2,86
|
32,83
|
204,02
|
|
860
|
-215,1
|
-210,8
|
124,77
|
-86,06
|
-82,72
|
-143,9
|
-124,5
|
55,25
|
-69,22
|
-2,61
|
|
2000
|
134,1
|
-637,7
|
690,06
|
52,33
|
-172,2
|
-227,9
|
-414,2
|
393,87
|
-20,36
|
-644,3
|
|
P, МВт
|
Uc1, кВ
|
Uc2, кВ
|
U2, кВ
|
Uc3, кВ
|
Uc4, кВ
|
|
kc = 0,4
|
|||||
|
860
|
528
|
516,38
|
517,15
|
520,14
|
513,64
|
|
1650
|
490,47
|
468,3
|
467,78
|
476,39
|
459,54
|
|
kc = 0,5
|
|||||
|
860
|
536,27
|
515,87
|
516,69
|
519,97
|
514,17
|
|
1720
|
517,18
|
483,02
|
477,79
|
485,05
|
472,28
|
|
1930
|
506,48
|
469,32
|
460,58
|
469,1
|
455,33
|
|
P, МВт
|
Q1, Мвар
|
Qk1, Мвар
|
Qxk1, Мвар
|
Qn2, Мвар
|
Qk2, Мвар
|
Qn3, Мвар
|
Qk3, Мвар
|
Qxk2, Мвар
|
Qn4, Мвар
|
Q3, Мвар
|
|
kc = 0,4
|
||||||||||
|
860
|
-223,2
|
-201,7
|
110,3
|
-91,5
|
-81,2
|
-145,4
|
-116,7
|
70,9
|
-45,8
|
82,7
|
|
1650
|
333,0
|
-487,8
|
461,6
|
-26,2
|
-196,3
|
-248,8
|
-382,7
|
384,2
|
1,4
|
-609,1
|
|
kc = 0,5
|
||||||||||
|
860
|
-276,1
|
-255,9
|
165,9
|
-90,0
|
-78,0
|
-142,1
|
-107,8
|
70,5
|
-37,3
|
86,3
|
|
1720
|
183,8
|
-631,4
|
712,0
|
80,6
|
-127,0
|
-181,8
|
-345,0
|
394,4
|
49,5
|
-558,1
|
|
1930
|
400,0
|
-761,9
|
939,5
|
177,6
|
-121,6
|
-172,6
|
-422,5
|
537,4
|
114,9
|
-816,6
|
|
P, МВт
|
Uc1, кВ
|
Uc2, кВ
|
U2, кВ
|
Uc3, кВ
|
Uc4, кВ
|
|
kc = 0,4
|
|||||
|
860
|
523,45
|
503,97
|
512,29
|
515,57
|
520,37
|
|
1230
|
492,67
|
495,62
|
472,9
|
513,39
|
487,69
|
|
P, МВт
|
Q1, Мвар
|
Qk1, Мвар
|
Qxk1, Мвар
|
Qn2, Мвар
|
Qk2, Мвар
|
Qn3, Мвар
|
Qk3, Мвар
|
Qxk2, Мвар
|
Qn4, Мвар
|
Q3, Мвар
|
|
kc = 0,4
|
||||||||||
|
860
|
-278,7
|
-265,9
|
136,32
|
-129,6
|
-81,24
|
-144,2
|
11,46
|
75,18
|
86,64
|
173,9
|
|
1230
|
57,37
|
-123,5
|
304,66
|
181,15
|
-143,9
|
-197,6
|
-360,1
|
212,02
|
-148,1
|
-216,2
|
|
P, МВт
|
Uc1, кВ
|
Uc2, кВ
|
U2, кВ
|
Uc3, кВ
|
Uc4, кВ
|
|
kc = 0,3
|
|||||
|
767
|
500
|
481,87
|
539,09
|
454,3
|
500
|
|
kc = 0,4
|
|||||
|
796
|
500
|
469,08
|
513,35
|
466,76
|
500
|
|
P, МВт
|
Q1, Мвар
|
Qk1, Мвар
|
Qxk1, Мвар
|
Qn2, Мвар
|
Qk2, Мвар
|
Qn3, Мвар
|
Qk3, Мвар
|
Qxk2, Мвар
|
Qn4, Мвар
|
Q3, Мвар
|
|
kc = 0,3
|
||||||||||
|
767
|
-347,1
|
-347,1
|
82,52
|
-264,5
|
-40,25
|
-110
|
320,63
|
107,93
|
428,56
|
428,56
|
|
kc = 0,4
|
||||||||||
|
796
|
-344,9
|
-344,9
|
175,25
|
-169,7
|
-88,57
|
-151,8
|
226,33
|
99,34
|
325,67
|
325,67
|
С целью верификации расчетов, произведенных в расчетном комплексе MathCAD и представленных ранее, была разработана схема линии электропередачи 500 кВ в ПК MatLab.
Проверка достоверности расчетов выполнялась для линии 500 кВ длиной 500 км, выполненная проводами марки 3хАС400/51 с соответствующими погонными параметрами. Расчеты проводились для степени компенсации 0,3 и режима передачи натуральной мощности.
Результаты расчета режима в MatLab представлены на рис. 1.3. Схема электропередачи и описание элементов ПК MatLab приведены в [1].
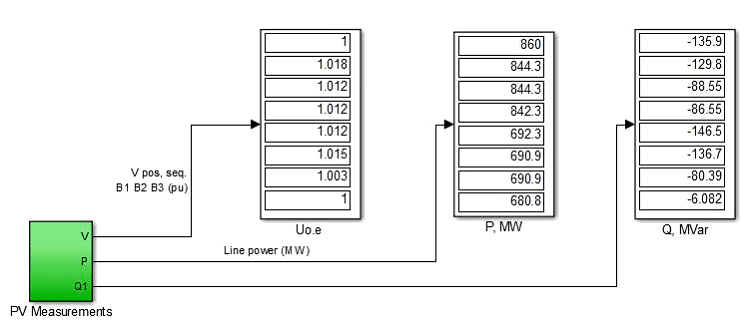
Сравнивая полученные результаты с данными из главы 3 табл. 3.4, 3.5, можно сделать вывод, что расчеты в MathCAD выполнены правильно, а схема замещения в MatLab построена верно, так как погрешность расчета напряжений составляет лишь 0,04% , а погрешность в расчете реактивных мощностей – 0,4 %.
Выполненные в работе исследования характеризуются следующими основными научными и практическими результатами:
1. Получены и проанализированы характеристики нормальных режимов линий электропередачи с двумя УПК и промежуточным отбором мощности.
2. При наличии двух УПК на линиях длиной 500-1500 км существуют оптимальные расстояния между ними, соответствующие наибольшей пропускной способности линии. Для линий длиной 300 км такие расстояния
не явно выражены и УПК могут располагаться как по концам линии, так и в средней точке.
3. При размещении двух УПК на оптимальном расстоянии между ними для линий длиной более 500 км напряжения на выводах конденсаторных батарей (КБ) в режимах холостого хода и малых нагрузок будут больше допустимых значений, что требует применения мероприятий по их снижению, например, установки шунтирующих реакторов на выводы КБ.
4. Выявлена зависимость изменения напряжений на выводах КБ от расстояния между УПК и определены расстояния, при которых эти напряжения не превышают допустимых значений во всех режимах при рассмотренных степенях компенсации. Расчеты производились при номинальном напряжении 500 кВ на приемной и передающей системах.
5. Успешно проведен эксперимент по моделированию длинной линии в ПК MatLab. Погрешности расчетов составляют менее 0,5%.
Библиографический список
- Шамардин А.О. Исследование влияния установки продольной компенсации на режимы работы дальней электропередачи: Магистерская диссертация.- НИУ МЭИ.
- Рыжов Ю.П. Дальние электропередачи сверхвысокого напряжения: Учебник для вузов. – М.: Издат. дом МЭИ, 2007.
- Рыжов Ю.П., Некукар А.Р. О возможности сооружения на линиях СВН устройств продольной емкостной компенсации без шунтирующих реакторов на выводах конденсаторных батарей. – Электричество, 2012, № 1.
- Зарудский Г.К., Радилов Т.В. Расчет установившихся режимов электропередачи сверхвысокого напряжения, оснащенной устройствами гибких электропередач. – Электричество, 2014, № 1.
- Зарудский Г.К. О результатах исследований по применению продольной емкостной компенсации в электропередачах СВН. – Электричество, 2007, № 9.
- Ивакин В.Н. Исследование характеристик управляемой продольной компенсации как устройства для регулирования потоков мощности гибких линий электропередачи переменного тока. – Электротехника, 2007, № 3.
- Поспелов Г.Е. Эффективность компенсирующих устройств для управления параметрами и режимами электрических сетей и их регулирования. – Изв. вузов и энергетических объединений СНГ. Энергетика, 2007, № 4.
