Одно из важных направлений прикладной математики связано с исследованием систем мaссового обслуживания (СМО). СМО – это системы, в которые в случайные моменты времени поступают заявки на обслуживание, при этом поступившие заявки обслуживаются с помощью имеющихся в распоряжении системы каналов обслуживания. Примерами СМО являются магазины, телефонные станции, кассы, ремонтные мастерские, автозаправочные станции, ЭВМ, обрабатывающая запросы от удаленных терминалов [1,7, 9].
При изучении СМО используются методы имитационного моделирования и статистических испытаний (или метод Монте-Карло). При этом создается компьютерная модель, имитирующая поведение системы, с помощью ее производят большое количество реализаций анализируемого процесса и сохраняют получающиеся значения выходных величин. Получающиеся результаты приобретают статистическую устойчивость и после соответствующей математической обработки могут рассматриваться как характеристики изучаемой системы [3,8,12,13]. Имитационные модели используются при изучении социологических, экономических процессов функционирования сложных технических систем (например, ядерного реактора), а также в процессе обучения.
Каждая из систем массового обслуживания состоит из каналов (или приборов) обслуживания, на которые в случайные моменты времени поступает поток заявок или требований. После приема заявки канал оказывается занят на некоторое время обслуживания , после чего он освобождается и ожидает следующей заявки. На входе СМО может накапливаться несколько заявок, они либо становятся в очередь, либо покидают СМО необслуженными [3,5].
Последовательность событий, происходящих друг за другом в случайные моменты времени, называется потоком событий. Если поток событий задается только моментами времени наступления этих событий, то он называется однородным. Поток неоднородных событий характеризуется:
- совокупностью вызывающих моментов времени ,;
- набором признаков событий, к которым относятся принадлежность заявки к тому или иному источнику, приоритет заявки, возможность обслуживания тем или иным каналом и т.д.
Интенсивность потока рассчитывается как отношение числа событий ко времени наблюдения: . В случае, когда вероятность появления заданного числа событий в течение интервала ∆τ зависит исключительно от продолжительности интервала ∆τ и не зависит от времени τ, прошедшего с начала запуска системы, поток событий называется стационарным [10,13].
Любая СМО состоит из приборов обслуживания , каждый из которых имеет накопитель заявок и канала обслуживания заявок . В накопители заявок может одновременно находится заявок, где –емкость i-ого накопителя. В накопитель поступает поток заявок , а в канал – поток обслуживаний . При изучение сложных систем массового обслуживания рассматривают специальные Q-схемы, образующие многоканальные и многофазные сети массового обслуживания. Связи между элементами таких СМО изображают в виде стрелок, которые показывают направления движения заявок. В некоторых случаях говорят о замкнутых СМО, имеющих обратную связь, по которой выходной поток обслуженных заявок снова поступает на вход того или иного прибора обслуживания. В общем случае процесс функционирования СМО любой сложности можно однозначно задать с помощью Q-схемы, учитывающей:
- множество входящих потоков W;
- множество потоков обслуживания U;
- правила R сопряжения элементов СМО;
- множество собственных параметров H;
- оператор алгоритмов обслуживания заявок A;
- вектором состояния Z, элементов которого характеризуют состояния всех приборов обслуживания и их накопителей.
Для изучения функционирования СМО методом статистических испытаний (методом Монте-Карло) стоится имитационная модель процесса и с помощью генератора случайных чисел производится «розыгрыш» случайных событий (входных сигналов и внешних воздействий) в соответствии с заданными законами распределения. Компьютер моделирует более 1000 реализаций исследуемого процесса, выходные сигналы и подвергаются статистической обработке.
Рассмотрим пример решения задачи о грузовой сортировочной станции в Arena и сравним с получившимися данными в Microsoft Excel.
На грузовой станции имеется два выгрузочных фронта. Интенсивность подхода составов под выгрузку составляет 0,4 состава в сутки. Среднее время разгрузки одного состава – 2 суток. Приходящий поезд отправляется на другую станцию, если в очереди на разгрузку стоят более трёх составов.
Оценить эффективность работы выгрузочных фронтов грузовой станции: вероятность, что выгрузочные фронты свободны, вероятность, что состав останется без разгрузки, относительную пропускную способность, абсолютную пропускную способность, среднее число поездов, ожидающих разгрузки, среднее число заявок в системе, среднее время пребывания заявки в очереди, среднее время пребывания заявки в системе. Как изменятся данные показатели, если интенсивность подхода составов увеличится до 0,5?
Решение таких задач, не смотря на разработанный математический аппарат, не очень удобно производить вручную. Для наиболее быстрого и эффективного решения, можно использовать различные программные средства: табличный процессор Microsoft Excel и среду имитационного моделирования Arena Rockwell Software. Табличный процессор при решении таких задач может помочь в вычислении приблизительных характеристик исследуемой СМО. Эти значения дают общее представление об эффективности работы системы и конечно не могут учесть массу случайных факторов, влияющих на ее работу. Кроме того, для многих подобных задач не менее важно представить логику работы системы, очереди, увидеть и понять какое количество поступивших составов получают отказ в обслуживании [5,6,8]. Эти вещи позволяет реализовать Arena (рис.1). Для решения задачи был выбран период моделирования равный 12 месяцам, что позволило получить представление о длительном периоде работы системы и наиболее приближенных к реальности показателях системы.
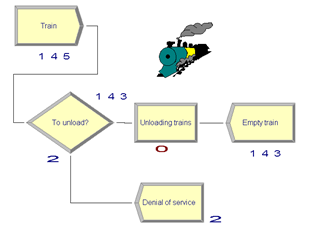
Рисунок 1. Логика задачи в Arena
По условию задачи n = 2, m = 3, т. е. грузовая станция представляет собой многоканальную систему с ограниченной очередью. Интенсивность потока обслуживаний равна μ =1/2 = 0,5. Интенсивность нагрузки канала (трафик) равна ρ = 0,4 ∙ 2 = 0,8. Теперь рассчитаем характеристики для интенсивности подхода составов, равной 0,4: вероятность того, что выгрузочный фронт свободен; вероятность того, что состав будет отправлен на другую станцию; относительную пропускную способность; абсолютную пропускную способность; среднее число составов, ожидающих разгрузки; среднее время ожидания разгрузки; среднее число занятых фронтов (среднее число заявок под обслуживанием); среднее число составов, находящихся у разгрузочного фронта; среднее время пребывания состава у разгрузочного фронта.
Произведем вычисления для интенсивности подхода составов, равной 0,4. Решение проиллюстрировано в таблице 1. Аналогично произведем вычисления для характеристик системы массового обслуживания с интенсивностью прихода составов равной 0,5.
Таблица 1 – Расчет характеристик для грузовой станции в Microsoft Excel
|
Характеристики многоканальной СМО с отказами |
||||
| Число каналов обслуживания | n |
2 |
2 |
|
| Максимальное число составов в очереди | m |
3 |
3 |
|
| Интенсивность прихода составов | λ |
0,4 |
0,5 |
|
| Время разгрузки 1 состава | tоб |
2 |
2 |
|
| Интенсивность разгрузки составов | μ |
0,5 |
0,5 |
|
| Приведенная интенсивность | ρ |
0,8 |
1 |
|
| Вероятность, того что канал свободен | P0 |
0,47 |
0,39 |
|
| Вероятность отказа в разгрузке | Pотк |
0,010 |
0,02 |
|
| Относительная пропускная способность | Q |
0,99 |
0,98 |
|
| Абсолютная пропускная способность | A |
0,40 |
0,49 |
|
| Длина очереди | Nоч |
0,14 |
0,29 |
|
| Среднее время в очереди | Tоч |
0,06 |
0,15 |
|
| Среднее число занятых каналов | k |
0,79 |
0,98 |
|
| Среднее время нахождения состава в системе | Nсист |
0,93 |
1,27 |
|
| Среднее число составов в системе | Tсист |
2,33 |
2,54 |
|
Сравнивая получившиеся результаты, можно сказать, что вероятность того, что состав будет отправлен на другую станцию при интенсивности подхода составов равной 0,5 больше, чем при интенсивности, равной 0,4.
Исходя из данных, приведённых данных в таблице 1 и получившихся результатах имитационного моделирования (в отчетах среднее время ожидания разгрузки - 9,5ч, а вероятность отказа 1,3%) можно сделать вывод о том, что среднее время пребывания состава в ожидании разгрузки на другой станции невелико, что говорит о нормальной работе разгрузочного узла. При увеличении интенсивности похода составов выгрузочный узел продолжает работать эффективно.
Используя данные программы, можно с легкостью обрабатывать большой массив данных, производить расчеты, наблюдать за многоканальной системой обслуживания в динамике, анализируя все ее слабые и сильные стороны. Помимо этого анимация процессов в программе Arena и обширные статистические данные, собранные в отчетах, помогут опытному пользователю быстро разобраться с причинами возникающих проблем в системе.
Библиографический список
- Акопов А.С. Имитационное моделирование: учебник и практикум. – Москва: Юрайт, 2015.–390 с.
- Баженов Р.И., Лопатин Д.К. Об имитационном моделировании экономических процессов средствами специализированной программной среды // Молодой ученый. 2014. № 4. С. 88-92.
- Гусева Е. Н. Математика и информатика: [электронный ресурс] учеб. пособие/ Е. Н. Гусева, И.Ю. Ефимова, И.Н. Мовчан, Л.А. Савельева. – 3-е изд., стереотип. –М.: Флинта, 2015– 400 с. –Режим доступа: lf5.com/Knigi/Nauka-Obrazovanie/Matematika/Matematika-i-informatika-148-103807
- Гусева Е.Н. Математические основы информатики/ Е.Н. Гусева, И.И. Боброва, И.Ю. Ефимова, И.Н. Мовчан, С.А. Повитухин, Л.А. Савельева. – Магнитогорск: Изд-во Магнитогорск. гос. техн. ун-та им. Г.И. Носова, 2016.- 234 с.
- Гусева Е. Н. Теория вероятностей и математическая статистика: учеб. пособие – 5-е изд., доп. и перераб.: [электронный ресурс]/ Е. Н. Гусева. –М.: Флинта, 2011.– 220 с. – Режим доступа: http://www.knigafund.ru/books/116083/read
- Гусева Е.Н. Имитационное моделирование экономических процессов в среде «Arena»: учеб. пособие: [электронный ресурс]. М.: Флинта, 2011. – 132 с. – Режим доступа: http://www.knigafund.ru/books/114189
- Гусева Е.Н. Имитационное моделирование социально-экономических процессов. – Магнитогорск: изд-во Магнитогорск. гос. техн. ун-та им. Г.И. Носова, 2015. – 25с.
- Гусева Е.Н. Моделирование макроэкономических процессов: учеб. пособ.: [электронный ресурс]/ Е. Н. Гусева. – М.: Флинта, 2014.–214с.– Режим доступа: http://www.ozon.ru/context/detail/id/28975354/
- Гусева Е.Н. Основы имитационного моделирования экономических процессов: лаб. практикум / Е.Н. Гусева. – Магнитогорск: МаГУ, 2007. – 140с.
- Кийкова Е.В. Управление системой закупок товаров, работ и услуг для нужд бюджетного образовательного учреждения на основе имитационного моделирования // Современные проблемы науки и образования. –2013. № 1. С. 302.
- Кийкова Е.В., Лаврушина Е.Г. Значение изучения имитационного моделирования студентами вуза различных уровней подготовки // Современные проблемы науки и образования. –2014. № 3. С. 388.
- Лебединский Б.П., Желекова Е.Э. Имитационное моделирование систем массового обслуживания в программном продукте GPSS // Вестник Курганского государственного университета. Серия: Технические науки. – 2012. № 24. С. 66-69.
- Самаров К. Л. Элементы теории массового обслуживания Учебное пособие для студентов [Электронный ресурс]. – URL: http://www.resolventa.ru/data/metodstud/servtheory.pdf (дата обращения: 19.06.2016).
