Метод последовательных испытаний применяется для контрольных испытаний на надежность систем и агрегатов самолета. Контрольные испытания позволяют лишь установить соответствие или несоответствие фактической надежности изделия согласованным требованиям к его надежности. При этом абсолютная оценка показателя надежности не производится, что обеспечивает снижение потребного для данной точности и достоверности объема испытаний.
Для получения подтверждения заданных требований по безотказности этим методом необходимы следующие исходные данные [1]:
- α-риск поставщика;
- β-риск потребителя;
- p0 – вероятность того, что партия считается годной в одном цикле;
- p1 - вероятность того, что партия считается негодной в одном цикле.
Эти исходные данные согласуются между поставщиком и потребителем авиационной техники. Для построения плана испытаний необходимо предварительно вычислить следующие параметры:
- оценочные нормативы А и В;
- константы плана h1, h2, S.
Для расчетов были использованы следующие формулы:
А=(1-β)/α , B=β/(1-α) , h1=lgB/{lg(q1/q0)+lg(1-q0)/(1-q1)},
h2=lgA/{lg(q1/q0)+lg(1-q0)/(1-q1)},
S=lg(1-q0)/(1-q1)/{lg(q1/q0)+lg(1-q0)/(1-q1)}, q1= 1 – p1, q0 = 1 – p0 .
Далее вычисляется минимальное число испытаний, при котором можно принять партию: m0=-h1/s . Вычислив m0 , можно построить график плана последовательных испытаний по трём характерным точкам(рис.1):
а) dm=0, m0=-h1/s; б) dm=h1, m=0; в) dm=h2, m=0 .
Как известно, план последовательных испытаний строится в виде графика (см. рис.1) или таблицы (табл.1).
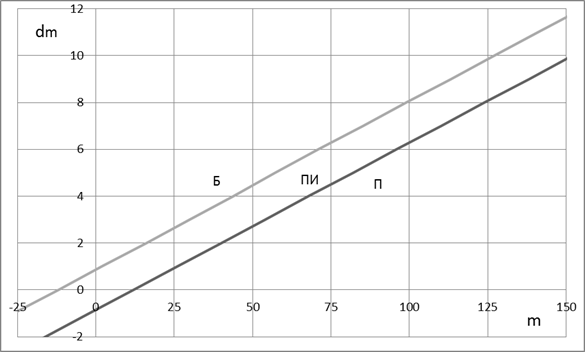
Рис.1. График плана последовательных испытаний:
m- число испытуемых агрегатов, dm- число отказавших агрегатов во время испытаний, П- линия приемки, Б- линия браковки, ПИ- продолжение испытаний.
Таблица 1
| dm | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| mпр, не более |
23 |
45 |
67 |
91 |
112 |
134 |
156 |
179 |
201 |
228 |
245 |
| mбр, не более |
– |
1 |
23 |
45 |
68 |
90 |
112 |
134 |
156 |
179 |
201 |
mпр-приёмочное число испытаний, mбр-браковочное число испытаний.
Рассмотрим влияние изменения значения исходных данных на план последовательных испытаний. Варьирования исходных данных производились в следующих диапазонах: p0 = 0,80…0,99, p1 = 0,80…0,99, α= 0,05…0,10, β= 0,05…0,10. Расчеты были выполнены в среде Microsoft Excel по вышеуказанным формулам [2].
Результаты расчетов сводятся в таблице. 2.
Таблица 2
| 1.Влияние изменения p0 = 0,99…0,80 на план последовательных испытаний (остальные параметры: p1=0,88; α=0,05; β=0,05; dm=5). | |||||||||||
| p0 | 0,99 | 0,97 | 0,95 | 0,9 | 0,9 | 0,89 | 0,87 | 0,85 | 0,83 | 0,81 | 0,80 |
| mпр, не менее |
135 |
106 |
101 |
107 |
136 |
304 |
-218 |
-48 |
-16 |
-3 |
1 |
| mбр, не более |
85 |
46 |
24 |
0 |
-40 |
-217 |
298 |
122 |
85 |
68 |
63 |
| 2.Влияние изменения p1 = 0,80…0,99 на план последовательных испытаний(остальные параметры: p0 = 0,99; α=0,05; β=0,05; dm=5). | |||||||||||
| p1 | 0,80 | 0,81 | 0,82 | 0,84 | 0,86 | 0,88 | 0,90 | 0,92 | 0,94 | 0,96 | 0,98 |
| mпр, не менее |
89 |
93 |
97 |
107 |
120 |
135 |
157 |
187 |
235 |
326 |
636 |
| mбр, не более |
61 |
63 |
66 |
71 |
78 |
85 |
95 |
107 |
121 |
135 |
56 |
| 3. Влияние изменения α= 0,05…0,10 на план последовательных испытаний(остальные параметры: p0 = 0,99; p1 =0,88; β=0,05; dm=5 ). | |||||||||||
| α | 0,05 | 0,053 | 0,055 | 0,06 | 0,065 | 0,07 | 0,075 | 0,08 | 0,085 | 0,09 | 0,10 |
| mпр, не менее |
135 |
135 |
135 |
135 |
135 |
135 |
135 |
135 |
135 |
135 |
135 |
| mбр, не более |
85 |
85 |
86 |
87 |
88 |
88 |
89 |
89 |
90 |
90 |
91 |
| 4. Влияние изменения β = 0,05…0,10 на план последовательных испытаний(остальные параметры: p0 = 0,99; p1 =0,88; α =0,05; dm=5 ). | |||||||||||
| β | 0,05 | 0,053 | 0,055 | 0,06 | 0,065 | 0,07 | 0,075 | 0,08 | 0,085 | 0,09 | 0,10 |
| mпр, не менее |
135 |
135 |
135 |
134 |
133 |
133 |
132 |
131 |
131 |
130 |
130 |
| mбр, не более |
85 |
85 |
86 |
86 |
86 |
86 |
86 |
86 |
86 |
86 |
86 |
В результате анализа полученных данных были сделаны следующие выводы:
- снижение значения вероятности того, что партия считается хорошей в одном цикле до p1 =0,91 приводит к уменьшению приёмочного числа испытаний и браковочного числа испытаний;
- с увеличением значения вероятности того, что партия считается негодной в одном цикле, увеличивается приёмочное число испытаний и медленнее увеличивается браковочное число испытаний;
- с увеличением значения риска поставщика α, увеличивается браковочное число испытаний, а приемочное число испытаний остается практически постоянным;
- с увеличением значения риска потребителя β, уменьшается приемочное число испытаний, а браковочное число испытаний остается практически постоянным.
Таким образом, полученные результаты могут быть использованы при составлении планов последовательных испытаний высокоресурсных агрегатов летательных аппаратов.
Библиографический список
- Косточкин В.В. Надежность авиационных двигателей и силовых установок. – М.: Транспорт, 1989.
- Половко А.М., Гуров С.В. Основы теории надежности. Практикум.- СПб.: БХВ-Петербург, 2006.
