Современная информатизация образования приводит к изменению форм, методов и средств школьного обучения. На первый план выдвигаются универсальные учебные действия, которые должны быть сформированы у учащихся. Использование компьютерных технологий в преподавании геометрии, к сожалению, оставляет желать лучшего. Это связано с нехваткой методических материалов по применению программных средств в обучении геометрии, а также недостаточной подготовкой педагогов-предметников в области компьютерных технологий.

Ученые считают, что успешность изучения геометрии зависит от двух составляющих: логического мышления и наглядно-образного воображения. К сожалению, для многих учащихся геометрия является одним из сложнейших предметов. Такие выводы позволяет сделать анализ результатов единого государственного экзамена по математике: большинство учащихся не пытаются решать задания, связанные с геометрией либо решают только плоскостные задачи. Очень малая доля учащихся пытается решить стереометрические задачи, не всегда достигая положительных результатов.

В чем же причина возникновения таких трудностей при изучении геометрии? Возможно, стоит обратить внимание на традиционную методику преподавания геометрии, заточенную в основном на развитие логического мышления.  Традиционные формы и средства обучения не достаточно эффективно развивают образное мышление, что порой и приводит к непониманию и пробелам в геометрических знаниях детей. Педагоги и методисты пытаются разработать современные методики преподавания геометрии, которые будут основаны на гармоничном формировании у школьников логического и наглядно-образного мышления. [1,8]

Использование возможностей компьютерного моделирования в школе позволит повысить эффективность усвоения многих геометрических знаний. Важно отметить, что его создание компьютерных моделей школьниками поможет им освоить навыки формализации условия задач, освоить современные способы и алгоритмы их решения и, конечно познакомиться с программными средствами для представления функциональных зависимостей, визуализации геометрических фигур [4,5,7] Компьютерное моделирование позволяет  создавать наглядные образы плоских и объемных геометрических фигур. Обучение с помощью компьютерного моделирования позволит не только рассмотреть объект под разными углами зрения, выполнить различные построения, сечения.

Применение современных программных средств при изучении геометрии позволит учащимся не просто  заучивать теоремы и формулы, а понимать, что за ними стоит, получать объемное представление об объекте, правильно воспринимать его свойства.  Опыт педагогов показывает, что именно визуализация с помощью ИКТ, наиболее эффективно помогает учащимся развивать осознание и представление геометрических объектов [2,3,6,8].

Очень важное качество компьютерного моделирования заключается в том, что при исследованиях с его использованием в результате эксперимента  обнаруживаются геометрические факты, которые будут новыми для учащихся. Это играет ключевую роль в обучении, т.к. дети гораздо быстрее воспринимают знания, полученные в результате эксперимента, чем просто логические выводы из учебника. Отметим также, что при самостоятельной разработке компьютерной модели учащиеся лучше разберутся в условии  задачи, зависимостях  между параметрами геометрических объектов, смогут увидеть новые способы ее решения.

Современные образование вносит свои коррективы в развитие интерактивных графических пакетов, которые позволяют выполнять геометрические построения, задавая разнообразнейшие соотношения между ними. Их можно разделить на два вида: программы двухмерной геометрии (2D) и программы трехмерной геометрии (3D), с помощью которых стало возможно получать двумерные и трехмерные геометрические модели, используя практически любой ПК.

Рассматривая варианты применения компьютерного моделирования на уроках геометрии, можно отметить два наиболее перспективных пути: использование Microsoft Excel и программы трехмерной геометрии GeoGebra.

GeoGebra – свободно-распространяемая (GPL) динамическая геометрическая среда, которая даёт возможность создавать «живые чертежи» в планиметрии и стереометрии, кроме того, у программы богатые возможности работы с функциями (построение графиков, вычисление корней, экстремумов, интегралов и т.д.) за счёт команд встроенного языка. Программа написана М. Хохенвартером на языке Java и распространяется бесплатно, обладает простым интерфейсом, имеет русскоязычную версию.

Рассмотрим пример использования GeoGebra для задачи на построение трапеции.

Задача 1. Даны два основания равнобедренной трапеции: АВ = 6 см, СD = 3 см и угол при основании, CAB = 60⁰ . Построить данную трапецию и найти ее площадь. Данная задача является плоскостной, поэтому выбираем инструмент «Полотно». Для решения задачи выделим шесть этапов.

1)       Для начала построим угол при основании CAB = 60⁰. Для этого построим прямую АЕ, выберем инструмент «Угол заданной величины» и отметим две точки, через которые проходит прямая. Появится окно, в которое нужно вписать величину угла.

2)       После этого, получим третью точку С. Проведем через вершину угла и новую точку прямую с помощью инструмента «Прямая».

3)       Построим основание трапеции АВ. Для этого нужно выбрать инструмент «Отрезок с фиксированной длиной», так как по условию задачи длина отрезка нам известна.

4)       Аналогично построим второе основание трапеции СD. Финальная часть построения – объединение точек В и С при помощи инструмента «Отрезок».

5)       Для нахождения площади трапеции требуются дополнительные построения. С помощью инструмента «Отрезок» проведем высоту из точки D к основанию АВ, получая тем самым отрезок DЕ.

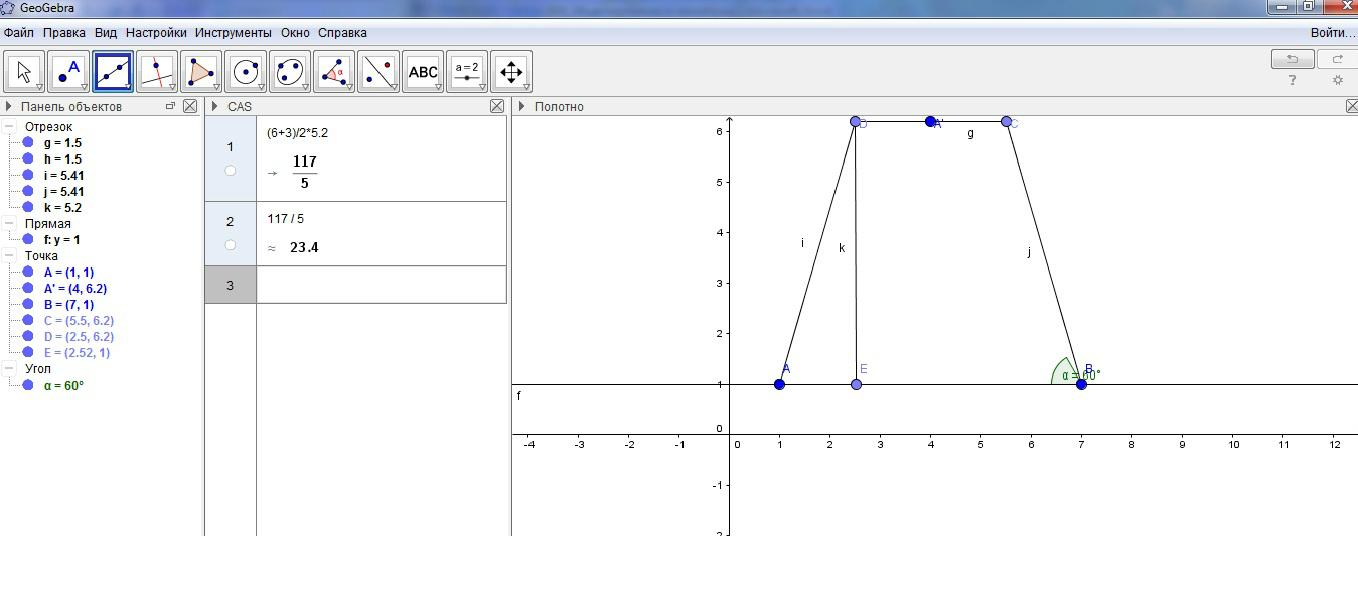
6)        Приступим к расчету площади трапеции. Данная программа отражает в инструменте «Панель объектов» значения всех длин сторон трапеции, что облегчает расчет. С помощью встроенной функции «Калькулятор» производится расчет, в результате  которого площадь трапеции равна 23,4 см². Все расчеты и пример построения приведены на рисунке 1.

Рисунок 1. Решение задачи о равнобедренной трапеции

Для большинства учащихся проблемой являются стереометрические задачи. Данная программа может упростить их решение, позволяя учащимся самостоятельно реализовать сложный процесс построения.

Задача 2. Известно, что радиус сферы равен 5,25 см. Построить сечение сферы. Данная задача является стереометрической, поэтому выбираем инструмент «Полотно 3D». Для начала построим сферу с радиусом 5,25 см.  Для этого выберем инструмент «Сфера по центру и радиусу».  Появится окно, в которое нужно вписать величину радиуса, после чего появляется нужная нам сфера.

На следующем этапе построим сечение сферы. Для этого нужно выбрать инструмент «Точка» и поставить точки, через которые будет проходить сечение. Далее выбираем «Плоскость через три точки». За несколько шагов можно выполнить сложное для учащихся задание. Пример построения приведен на рисунке 2.

Рисунок 2. Построение сечения сферы

Microsoft Excel – табличный процессор, программа для выполнения  вычислений и графического представления их результатов. Microsoft Excel или же ее аналоги Open Office Calc, LibreOffice Calc  существуют в открытом доступе, обладают интуитивно понятным интерфейсом, большим набором математических, статистических, логических и других встроенных функций, а также средствами создания графиков и диаграмм. Создание компьютерных математических моделей в среде Microsoft Excel поможет учащимся быстрее запомнить формулы и выявить существующие закономерности, проанализировать этапы построения фигур.

Рассмотрим построение эллипса в  Microsoft Excel.

Задача 3. Даны координаты центра эллипса (3;2) и значения большой и малой полуосей a=5 см и b=7 см.  Построить эллипс.

Обсуждая решение задачи с учащимися, нужно вспомнить уравнение эллипса с центром в начале координат и с центром в точке (x₀;y₀).

х^2/а^2 + у^2/b^2 =1

(х-х_0)^2/а^2 +( у-у_0)^2/b^2 =1

Для построения эллипса будем использовать 20 точек с углом окружности от 0  до 2π. Также зададим координаты центра эллипса (3;2) и значения большой и малой полуосей (3 и 4 соответственно).  Для построения эллипса рассчитаем значения х и у. Координата х считается по формуле: х₀+a*cos(a), координата y рассчитывается по формуле:  y₀+b*sin(a). Нужно ввести соответствующие формулы в ячейки таблицы, установив где требуется абсолютные ссылки. Затем построим график эллипса, выбирая точечную диаграмму с гладкими  кривыми как на рисунке 3.

Рисунок 3. Построение эллипса в Microsoft Excel.

Таким образом, использование широких возможностей современных программных средств позволяет изменить традиционные подходы к изучению многих вопросов геометрии. Самостоятельное создание компьютерных моделей учащимися позволяет развивать не только логическое мышление, но и пространственное воображение, формировать у детей навыки анализа и представления математических данных.  Качественно новые дидактические возможности современных программ позволяют повысить эффективность освоения школьниками основ геометрии.

1. Андрафанова Н.В., Назарян Д.С. Интерактивная геометрическая среда как средство компьютерной наглядности в обучении геометрии. Материалы международной научно-практической конференции «Информационные технологии в обеспечении федеральных государственных образовательных стандартов», Елец, 2014, с.76-80.
2. Вовк И.Г. Геометрическое моделирование линейных объектов в прикладной геоинформатике // Вестник СГУГиТ (Сибирского государственного университета геосистем и технологий). 2013. №4 (24). URL: http://cyberleninka.ru/article/n/geometricheskoe-modelirovanie-lineynyh-obektov-v-prikladnoy-geoinformatike (дата обращения: 07.06.2016).
3. Гусева Е. Н. Дидактические условия использования педагогических программных средств в процессе профессиональной подготовки будущих учителей: дисс. кан. пед. наук. – Магнитогорск: МаГУ, 1999. – 168 с.
4. Гусева Е. Н. Математика и информатика: [электронный ресурс]  учеб. пособие/ Е. Н. Гусева, И.Ю. Ефимова, И.Н. Мовчан,  Л.А. Савельева. – 3-е изд., стереотип. –М.: Флинта, 2015– 400 с. –Режим доступа:  lf5.com/Knigi/Nauka-Obrazovanie/Matematika/Matematika-i-informatika-148-103807
5. Гусева Е.Н. Математические основы информатики/ Е.Н. Гусева, И.И. Боброва, И.Ю. Ефимова, И.Н. Мовчан, С.А. Повитухин, Л.А. Савельева. – Магнитогорск: Изд-во Магнитогорск. гос. техн. ун-та им. Г.И. Носова, 2016.- 234 с.
6. Гусева Е.Н. Моделирование макроэкономических процессов: учеб. пособ.: [электронный ресурс]/ Е. Н. Гусева. – М.: Флинта, 2014.–214с.– Режим доступа: http://www.ozon.ru/context/detail/id/28975354/
7. Гусева Е.Н. Основы имитационного моделирования экономических процессов: лаб. практикум / Е.Н. Гусева. – Магнитогорск: МаГУ, 2007. – 140с.
8. Кайгородцева Н.В. Геометрия, геометрическое мышление и геометро-графическое образование // Современные проблемы науки и образования. – 2014. – № 2.; URL: http://www.science-education.ru/ru/article/view?id=12330 (дата обращения: 16.06.2016).

Все статьи автора «Ермакова Татьяна Александровна»