Понятие функции является одним из основных в науке и имеет мировоззренческое и общекультурное значение. Благодаря ему можно изучать физические величины в их взаимосвязи, а с помощью свойств функций решать математические задачи. Кроме того, изучение естествознания и техники также немыслимо без функций. Их широкая применимость обусловила введение учения о функциях в школьный курс математики.

Еще в XVII веке идея функции встречается у Рене Декарта. Он ввел данный термин в 1673г., и понятие функции первоначально носило геометрический характер. С появлением таких ученых, как Бернулли и Эйлер, понятие функции приобретает аналитический характер. Современное определение функции трактуется как соответствие между множествами любой природы, в курсе алгебры оно имеет название – определение Дирихле-Лобачевского.

С течением времени были хорошо изучены элементарные функции, которые теперь изучаются в школе.

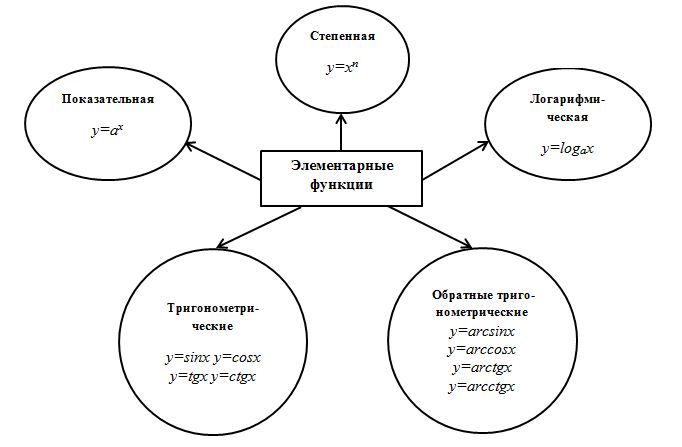
Функция называется элементарной, если ее значения могут быть получены из постоянных чисел и значений независимых переменных посредством конечного числа элементарных операций [1, с.13]. В их число входят следующие функции (Рисунок 1):

1)    алгебраические функции (степенные с любым действительным показателем);

2)    трансцендентные функции (показательная и логарифмическая функции, тригонометрические и обратные тригонометрические функции).

Рисунок 1. Элементарные функции

Трактовки понятия функция делятся на 2 вида:

1)                классические – опираются на понятие переменной величины (функция – переменная величина, числовое значение которой изменяется в зависимости от числового значения другой [2, с. 258]);

2)                современные (если каждому элементу х множества М поставлен в соответствие некоторый элемент y множества N, то говорят, что на множестве М задана функция, и пишут: у=f(x) [3, с.2]).

Классическое определение, называющее функцией переменную величину, зависящую от другой переменной величины (аргумента), подходит  к обычным аналитическим числовым функциям, изучаемым в школьном курсе математики, является традиционным и часто применяется в преподавании.

Стоит обратить внимание и на базовые модели теории функций. В их число входят функции, определенные на данных множествах:

1)                на числовом множестве;

2)                на множестве точек геометрического пространства;

3)                на множестве двоичных последовательностей;

4)                на множестве векторов;

5)                на множестве геометрических фигур;

6)                на множестве событий.

Проблема изучения понятия функции в школе является очень актуальной. Многие педагоги и методисты выделяют его как фундаментальное математическое понятие. Стоит отметить выступление педагога высшей немецкой школы Феликса Клейна, который главной целью обучения ставил необходимость обеспечить усвоение понятия функции еще на ранних этапах. По его мнению, оно должно пронизывать все преподавание алгебры и геометрии, то есть играть руководящую роль в школьном курсе математики.

И все же несомненную ценность представляет и ряд других понятий, которые должны получить самостоятельное развитие в ходе обучения. В их числе находятся понятия следующих содержательно-методических линий: линии числа, преобразований курса алгебры и начал анализа, линии уравнений, неравенств и их систем. Немаловажно также развитие логического мышления учащихся. Нет необходимости выделять какую-либо одну из представленных идей школьного курса математики и давать ей развитие за счет других, ведь все эти теории изучаются во взаимосвязи.

Безусловно, изучение функций развивает функциональное мышление учащихся, дети знакомятся с идеей всеобщей непрерывности, бесконечности, формируют у себя умения анализировать, находить зависимости между изменениями различных объектов, работать с абстрактным материалом. Изучение свойств функций позволяет познавать явления окружающего мира. Но в младших классах ученики могут оказаться неподготовленными к восприятию понятия функции в силу своего недостаточного математического развития. Это только повлечет за собой затраты времени на дополнительное объяснение, что ставит под сомнение идею Ф. Клейна.

В школе основное внимание уделяется числовым функциям. Понятие соответствия, лежащее в основе определения понятия функции, доступно учащимся 5 класса. При решении текстовых задач ученики используют различные функциональные зависимости.

Среди зависимостей наиболее часто встречаются следующие:

1)                цена, вес и стоимость;

2)                скорость, время и расстояние;

3)                стороны прямоугольника и его площадь;

4)                стороны прямоугольника и его периметр;

5)                работа, время работы и оплата и т. д.

Необходимо заранее подготовить учеников к осмысленному усвоению понятия функции и идеи функциональной зависимости. Для этого используются специально подобранные упражнения, которые направлены на накопление учениками опыта, на активацию их образного мышления. Очень важно, чтобы учащиеся поняли, что выражение, которое они рассматривают, будет принимать разные значения в зависимости от числовых значений переменных. Такие упражнения способствуют пониманию учениками различных способов выражения функциональной зависимости. Кроме того, важным аспектом изучения функций является введение понятия множества. Именно данный термин предшествует формулировке понятия функции. Выяснение понятия «множества» целесообразно производить не сразу на математических примерах, а начиная с более простых, например: совокупность парт в кабинете, письменных принадлежностей в пенале, учеников в классе. А затем постепенно можно вводить и такие термины, как элементы множества, подмножество, принадлежность множеству и др.

В школе чаще всего используются аналитический и формальный походы к изучению функций, поэтому учащиеся запоминают определения и формулировки свойств, не подкрепляя их образами. Нужно больше внимания уделять графикам функций, с их помощью легче будет понять многие свойства функций, такие, как нули функции, монотонность, область значений функции.

Понимание функции как математической модели реальных процессов определяет общекультурный аспект изучения математики. В связи с этим учащиеся должны уметь видеть функциональную зависимость не только в алгебраических формулах, но и в других школьных предметах и в жизни. Такое построение учебного материала отвечает принципу целостности образования[2, с.264].

Сформированность понятия функциональной зависимости у учащихся –  это важная задача целевой деятельности педагога. Она направлена на становление математического мышления и развитие творческой деятельности учеников. Развитие функционального мышления главным образом предполагает формирование способностей к овладению общими учебными приемами и умениями, обнаружению новых связей.

1. Энциклопедия элементарной математики: Книга 3, Функции и пределы (основы анализа) / под ред. Александрова П.С., Маркушевича А.И., Хинчина А.Я.  – М. : Государственное издательство технико-теоретической литературы, 1952. – 559 с;
2. Методика и технология обучения математике. Курс лекций: пособие для вузов / под научн. ред. Н.Л. Стефановой, Н.С. Подходовой. – М.: Дрофа, 2005. – 416 с. : ил.;
3. Маркушевич А.И. Понятие функции / А.И. Маркушевич // Математика в школе. – 1947. – № 4. – с. 1-17;
4. Новоселов С.И. Учение о функциях в средней школе / С.И. Новоселов // Математика в школе. – 1946. – № 5-6. – с. 22-38;
5. Тарасова В.А. Функциональная пропедевтика на уроках математики в 5-6 классах / В.А Тарасова // Педагогика. – URL: http://knowledge.allbest.ru/pedagogics/2c0a65625b2bc78a4d53b89521306c37_0.html (дата обращения: 17.04.16);
6. Колмогоров А.Н. Что такое функция / А.Н. Колмогоров // Квант. – 1970. – № 1. – с. 27-35;
7. [Электронный ресурс]. – URL: http://urokimatematiki.ru/7klass/item/1148-chto_takoe_funkcija.html (дата обращения: 21.04.16)

Все статьи автора «Титарева Галина Александровна»