Введение 

В научном сообществе доминирует убеждение о том, что атом водорода является самым простым. И существующие теории на основе уравнений Шредингера и Дирака полностью описывают все тонкости поведения электрона в атоме водорода.
В данной работе и в следующих статьях будет показано, что кроме известных состояний основанных на решениях уравнений Шредингера и Дирака , существуют состояния которые небыли изучены и небыли известны. Или часто просто отбрасывались с формулировкой “не имеют физического смысла”. 
Далее будет показано, что существующие уравнения квантовой механики а именно уравнение Дирака, уравнение Клейна-Гордона и тем более уравнение Шредингера, не могут точно описывать все тонкости поведения электрона в атоме водорода. 
В результате будут приведены достаточно оснований для целесообразности экспериментального поиска или целенаправленного синтеза новых неизвестных состояний атома водорода.

Данную статью можно скачать в формате PDF по ссылке - https://portalnp.snauka.ru/wp-content/uploads/2016/06/ExoticHatom1.pdf

Решение уравнения М2 для атома водорода

В работе [1] приведен вывод нового релятивистского уравнения М2 (1.1). Далее приводится решение уравнения для водорода и для изоэлектронного ряда в основном состояний при значении квантового числа .

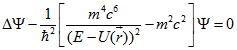 (1.1)

Теперь приведем решение уравнения М2 с учетом всех возможных значений квантового числа .
Для решения уравнения (1.1) применим стандартную методику разделения переменных в сферической системе координат.
В центральном поле ядра атома водорода потенциальная энергия электрона зависит только от одной координаты, расстояния от центра.  (1.2)

Представим волновую функцию в виде произведения радиальной и угловой частей  (1.3)
Оператор Лапласа в сферических координатах выглядит следующим образом:   (1.4) Подставим произведение (1.3) и потенциальную энергию (1.2) в исходное уравнение (1.1).
 Умножим полученное уравнение на дробь . 
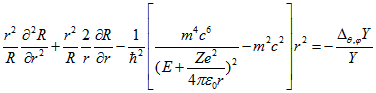 (1.5) Как можно заметить левая часть уравнения (1.5) зависит только от переменной , а правая от переменных  и . Следовательно, обе части равны некоторому постоянному числу . Что позволяет отделить радиальную часть уравнения от угловой части.
 (1.6)  (1.7) Далее представим функцию  в виде произведения  (1.8). Угловая часть оператора Лапласа имеет следующий вид:  (1.9). Подставим произведение (1.8) в угловое уравнение (1.7) получим:  (1.10).
Умножив уравнение (1.10) на дробь  получим:  (1.11). Левая часть уравнения (1.11) зависит только от переменной  а правая часть только от переменной . Следовательно, обе части равны некоторому постоянному числу, которую обозначим (не спутать с массой электрона). В итоге получим два уравнения:  (1.12) и  (1.13)
Решение уравнения (1.13) хорошо известно  (1.14). Так как при тождественных значениях угла  ( и ) функция должна иметь одно и то же значение, то  и . Используя формулу Эйлера для комплексных чисел: , получим  Таким образом,  может принимать только целочисленные значения. Константа находится из условия нормировки функции .
 (1.15) откуда следует  и  окончательно получим нормированную функцию в виде  (1.16)
Для решения уравнения (1.12), воспользуемся математическим интернет ресурсом WolframAlpha http://www.wolframalpha.com/ 
Решение дает:  (1.17)
То есть, решением является, сумма присоединенных функций Лежандра первого и второго рода.
Сделаем обозначение  (1.18). Переменная  у нас будет ассоциироваться с азимутальным квантовым числом. Определим область возможных значений квантового числа . Из формулы (1.18) следует, что  следовательно  (1.19). Переписав зависимость (1.18) относительно  получим  (1.20) как и следовало ожидать. Таким образом угловая часть волновой функции будет иметь вид:
 (1.21)

При традиционном описании орбитального углового момента квантовые числа  и принимают целые значения. В этом случае функция  имеет особенности. Поэтому принимается . Кроме того считается, что квантовое число  не может принимать отрицательное значение. Такой подход автоматический исключает рассмотрение возможных решений уравнения при значении квантового числа . Которое согласно соотношению (1.19) не является запрещенным.
Теперь мы поднимем этот вопрос и покажем, что при надлежащем подходе можно получить неразрывную волновую функцию (1.21) при значениях квантовых чисел  и .
Функция  при значениях  и  имеет сингулярность на полюсе при . А функция  при значениях  и  имеет сингулярность на полюсе при . Поэтому поступим следующим образом: Разделим область возможных значений переменной  на два интервала  и 
В первом интервале поведение электрона будет подчиняться функции Лежандра первого рода  а во втором интервале поведение электрона будет подчиняться функции Лежандра второго рода .
А соответствующее переключение между функциями будет осуществлено посредством выбора констант интегрирования  и . То есть в первом интервале   а во втором интервале  .
В результате получим следующую картину:

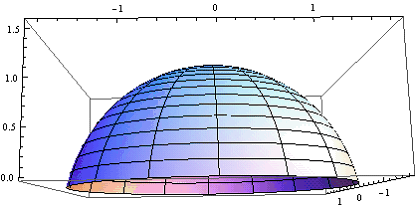
Рис.1 График функции  при  и  в интервале 

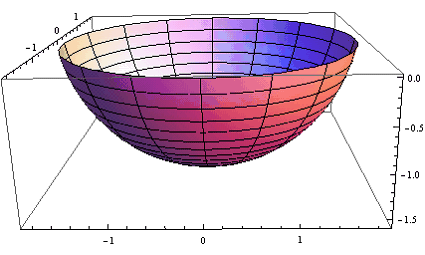
Рис.2 График функции  при  и  в интервале 

Теперь объединим вместе оба графика на одном рисунке. Рис. 3

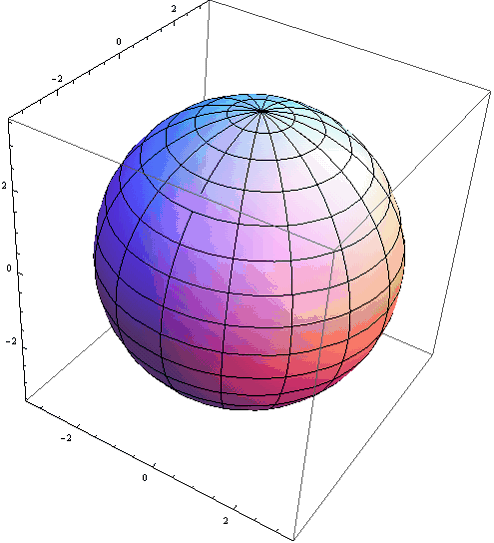
Рис. 3 График угловой части волновой функции (1.21) при соответствующем выборе констант интегрирования и интервалов для переменной .

Таким образом, как было сказано, при надлежащем подходе можно получить гладкую, неразрывную функцию в качестве угловой части волновой функции (1.21). 
Образно говоря, электрон не зайдет в зону сингулярного поведения волновой функции а совершит “обходный маневр”. 
Другим аргументом в пользу рассмотрения состояния с квантовыми числами  и  является то обстоятельство, что несмотря на наличие сингулярностей на полюсах, угловая волновая функция (1.21) квадратично интегрируема. То есть интеграл от квадрата модуля  сходится.
Поскольку в сферической системе координат элемент телесного угла , то на полюсах при  и  получим . Следовательно умножение на  устраняет сингулярность.
Приведем для наглядности график функции  при  и ,,  Рис.4.

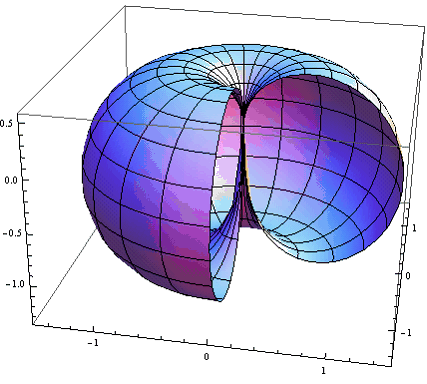
Рис.4. График функции  при  и ,, 

График приведен в частично разрезанном виде чтобы было заметно поведение функции во внутренней области. Как видим, представляет из себя полую тороидальную поверхность без какой либо сингулярности. Точно такой же график получается для функции Лежандра второго рода  и для их суммы.
Перейдем к решению радиального уравнения М2 (1.6). Для этого воспользуемся математическим интернет ресурсом WolframAlpha http://www.wolframalpha.com/ 
Перепишем уравнение (1.6) с учетом обозначения (1.20).
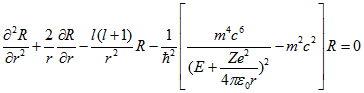 (1.22)
Далее будем применять атомную систему единиц Хартри. Перепишем уравнение (1.22) в атомных единицах Хартри.

 (1.23)
Решение уравнения (1.23) представляет из себя сумму двух линейно независимых частей. Обобщенных полиномов Лагерра и вырожденной гипергеометрической функции второго рода.
Воспользуемся первым линейно-независимым решением. Который имеет вид:

 где обобщенный полином Лагерра, константа интегрирования.  где  квантовое число.
Как известно, первый параметр обобщенного полинома Лагерра является радиальным квантовым числом . Из этих соображений, получаем уравнение для определения энергии основного состояния и возбужденных состояний водородоподобных ионов в следующем виде: 
(1.24)
Решая уравнение (1.24) с параметрами  определим энергию исследуемого состояния атома водорода. Решение дает значение энергии  в атомных единицах Хартри. Полученная энергия включает в себя энергию покоя электрона . Учитывая это, определим энергию исследуемого состояния и преобразуем ее в электрон-вольты.  а.е. В электрон-вольтах получим .
Определим константу интегрирования пользуясь условием нормировки 
 Используя формулу для радиальной волновой функции, построим график нормированной радиальной плотности вероятности Рис. 5.

 

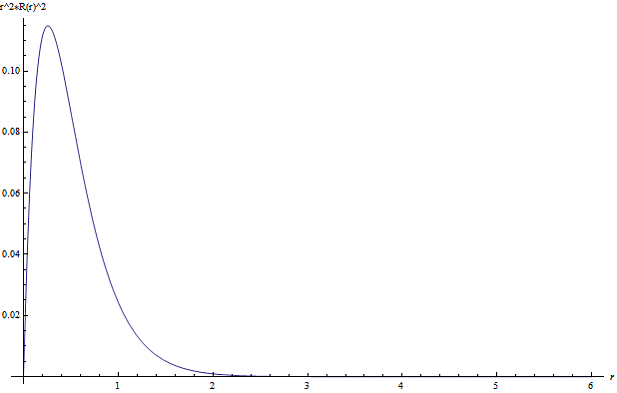
Рис.5 Нормированная радиальная плотность вероятности при 

Определим орбитальный радиус, то есть расстояние от начала координат до точки максимума плотности вероятности.  в атомных единицах. Умножив полученное значение на радиус Бора  получим . И соответствующий максимум получим .
Таким образом путем решения уравнения М2 была доказана возможность существования неизвестного до настоящего времени состояния для атома водорода со следующими параметрами: Значение квантовых чисел , , . Значение энергии состояния . Значение орбитального радиуса .
Обозначим полученное состояние атома водорода символом  и назовем “Водород с нулевой валентностью” [2], так как полученные характеристики не позволяют вступать  в химические соединения.
Построим график радиальной волновой функции  Рис.6.

Рис.6 График радиальной волновой функции при 

Как видим волновая функция стремится к бесконечности при . Но такое поведение нельзя считать не физическим. Потому что, это следствие бесконечного роста в отрицательную сторону Кулоновского потенциала при  . В реальности же, потенциал отличается от чисто Кулоновского при  и является ограниченным снизу, так как ядро не является точечным а имеет размеры. 
Отметим, что и другие уравнения квантовой механики тоже имеют аналогичные решения. Приведем в виде таблицы эти данные для сравнения, без подробного изложения соответствующих решений.

РЕЗУЛЬТАТЫ
решений уравнений квантовой механики для атома водорода H°
No	Уравнение	Энергия в атомных единицах	Энергия эВ	Орбитальный радиус в атомных единицах	Орбитальный радиус пм
1	M2	-1.94376843	-52.8705013	0.25721897	13.60688351
2	Дирака	-2.00010651	-54.40289707	0.24997349	13.22359762
3	Клейна-Гордона	-1.99840364	-54.35657901	0.25012141	13.23142259
4	Шредингера	-2	-54.4	0.25	13.225

Как можно заметить, результаты решений в основном достаточно точно совпадают для уравнений Дирака, Клейна-Гордона и Шредингера. Для уравнения М2 имеется довольно ощутимое различие. Возможно в дальнейшем, при экспериментальном поиске, именно это различие позволит правильно идентифицировать состояние водорода .

Уравнение М2 в цилиндрических координатах

Приведенные в первом разделе аргументы в пользу неразрывности угловой части волновой функции, могут быть недостаточно убедительными. Поэтому в этом разделе попытаемся предоставить дополнительные доказательства существования экзотического состояния атома водорода с полученными выше параметрами.
Перепишем уравнение М2 (1.1) в цилиндрических координатах. Оператор Лапласа в цилиндрических координатах выглядит следующим образом: 
 (2.1) Потенциальная энергия в цилиндрических координатах имеет вид  (2.2) . Подставляя полученные выражения в уравнение (1.1) получим: 
 (2.3)
Представим волновую функцию в виде произведения  (2.4). Подставим произведение (2.4) в исходное уравнение (2.3).

 (2.5)
Умножим полученное уравнение на дробь . 

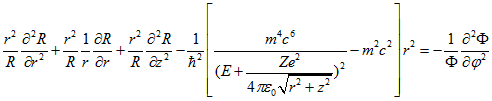 (2.6)
Далее будем применять атомную систему единиц Хартри. Перепишем уравнение (2.6) в атомных единицах Хартри.
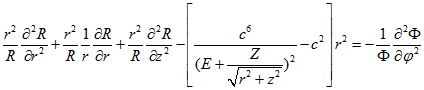 (2.7)
Как можно заметить левая часть уравнения (2.7) зависит только от переменных  и а правая от переменной . Следовательно, обе части равны некоторому постоянному числу которое обозначим  (не спутать с массой электрона). Что позволяет отделить радиальную часть уравнения от угловой части. В итоге получим два уравнения: 

 (2.8)  (2.9)
Полученное уравнение (2.9) совпадает с уравнением (1.13) поэтому имеем решение  (2.10) и значения для 
Поскольку мы анализируем состояние с квантовым числом , то получим значение волновой функции . А уравнение (2.8) примет вид:

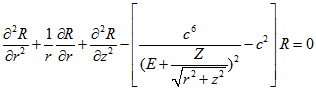 (2.11) Полученное уравнение не содержит угловую часть в явном виде. Поэтому проблема неразрывности угловой части снимается автоматический. Но при этом необходимо убедиться в сходимости решения уравнения (2.11) при значении энергии состояния .
Решить уравнение (2.11) аналитическими методами будет затруднительно. Поэтому применим для решения численные методы. Будем пользоваться пакетом программ для численного решения систем дифференциальных уравнений FlexPDE http://www.pdesolutions.com/
В результате численного решения получены следующие значения параметров водорода в состоянии .   
Что достаточно хорошо согласуется с данными аналитического решения.
Численное решение показало:1. Уравнение для состояния водорода  имеет достаточно высокую сходимость. 
2. Беспокойства по поводу сингулярного поведения угловой части волновой функции беспочвенны.
3. Следовательно имеются достаточно оснований для целесообразности экспериментального поиска водорода в состоянии .Ниже приведем результаты решения в виде двумерных и трехмерных графиков волновой функции и радиальной плотности вероятности.

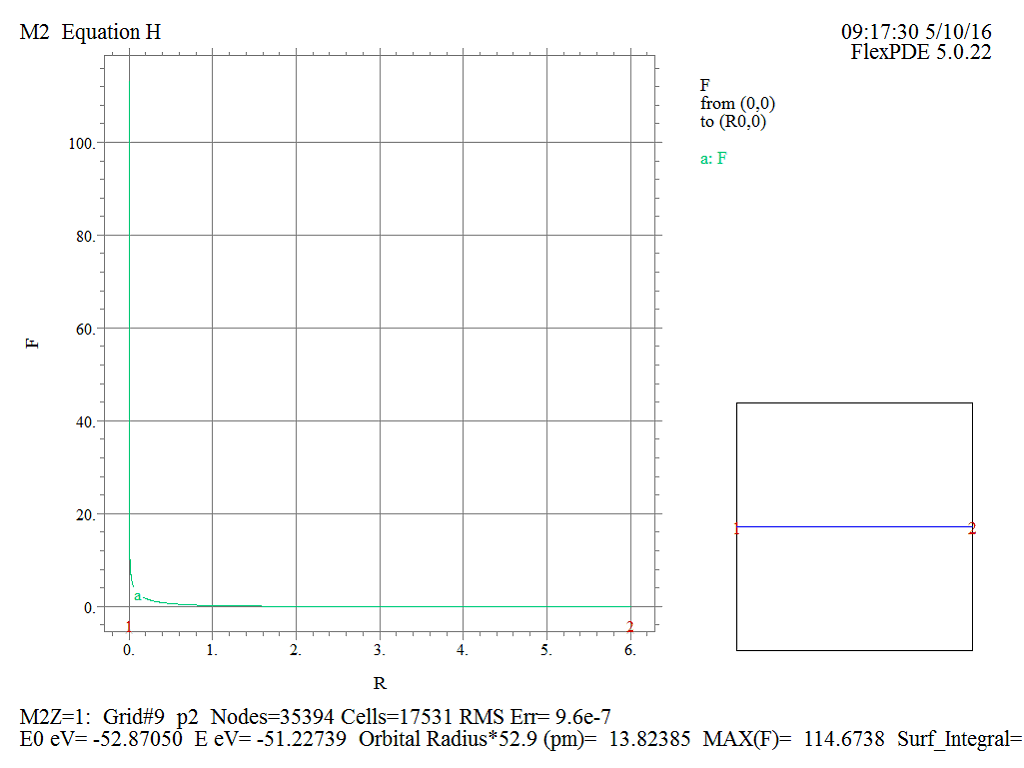
Рис.7 Двумерный график волновой функции

Рис.8 Трехмерный график волновой функции

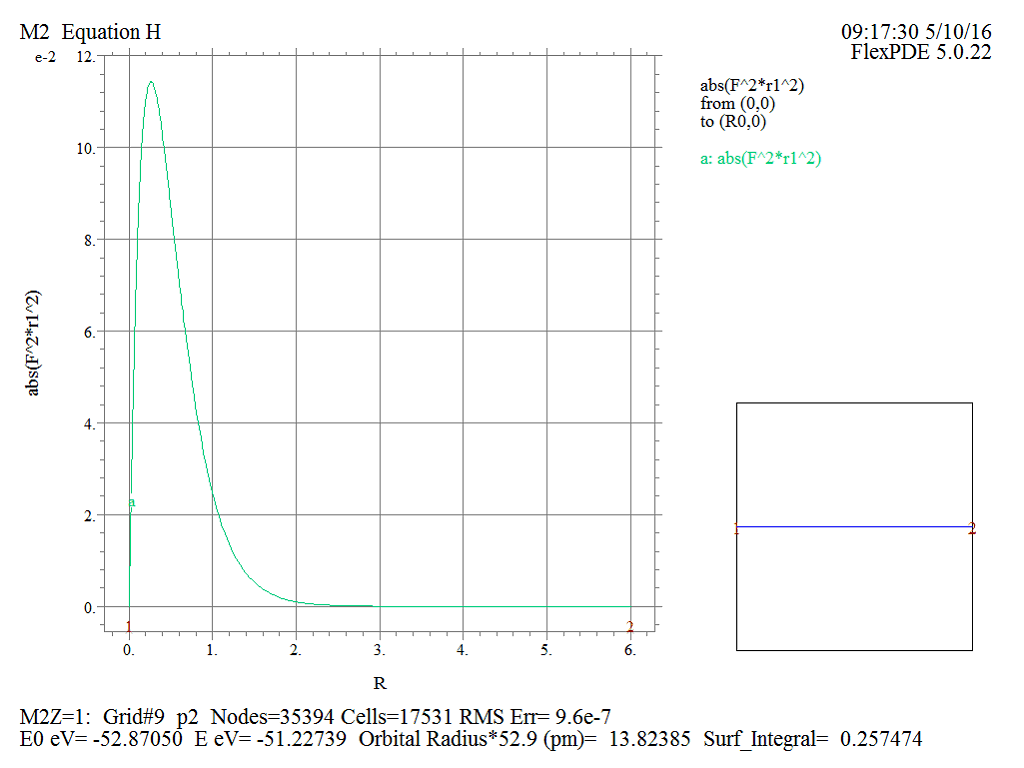
Рис.9 Двумерный график радиальной плотности вероятности
Рис.10 Трехмерный график радиальной плотности вероятности

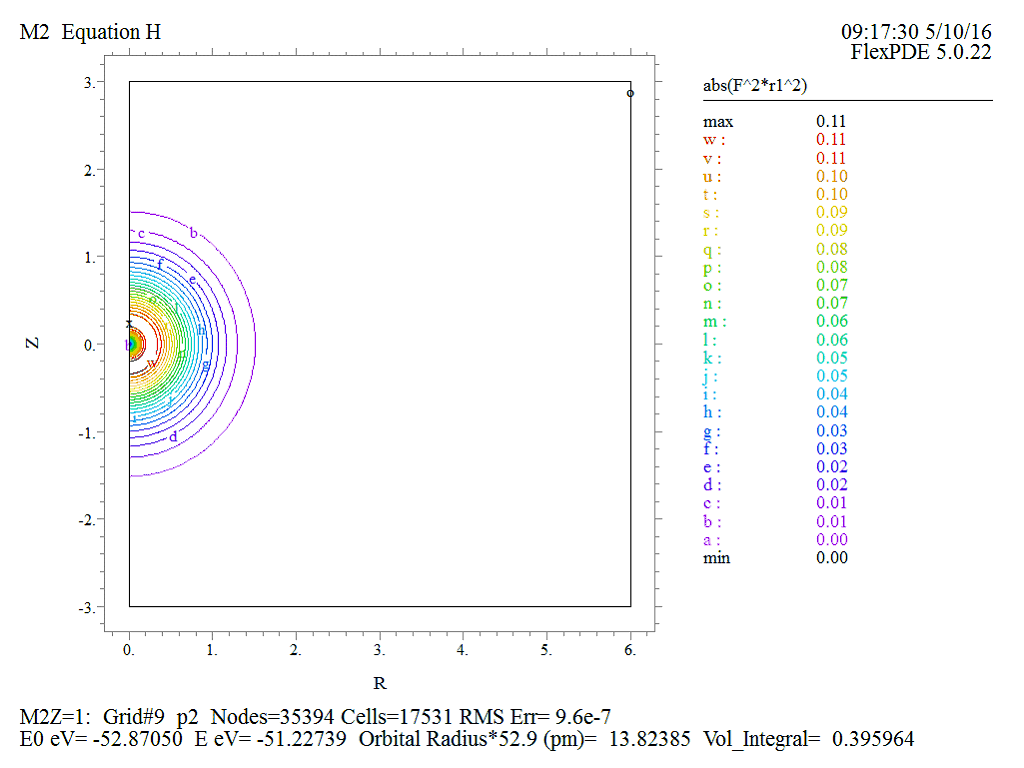
Рис.11 Проекция трехмерной радиальной плотности вероятности

Результаты и обсуждения

Споры вокруг атома водорода не утихают до сих пор. Казалось бы, после создания квантовой механики и решения уравнений Шредингера и Дирака все вопросы должны были бы исчезнуть уже давно. Однако время от времени возникают гипотезы относительно существования у атома водорода энергетических состояний с энергией ниже так называемого основного состояния. В частности такую гипотезу развивает в своих теориях и экспериментах 
доктор Randell Mills основател компании Brilliant Light Power, Inc. (BLP). 
Существуют многочисленные работы за и против. Также существуют экспериментальные результаты с высвобождением огромных количеств энергии, необъяснимые с позиции современной науки. Примером такого эксперимента может служить устройство изобретателя Аракелян Г.Г. [2]. 
Настоящая работа показывает, что все эти разговоры не беспочвенны. Существование состояний атома водорода с энергией ниже основного состояния в математическом отношении вполне возможно. Может быть против этого существуют другие чисто физические причины? Но то что имеются достаточно оснований чтобы основательно разобраться в этом вопросе, не вызывает сомнения. 
Теоретические работы в этом направлении будут продолжены.

Библиографический список

1. Дангян А.Э. “Новое уравнение релятивистской квантовой механики”
2. Водород нулевой валентности    Аракелян Г.Г.
3. Дангян А.Э. “Позитроний”

---

Количество просмотров публикации: Please wait

Все статьи автора «Дангян Араик Эмильевич»