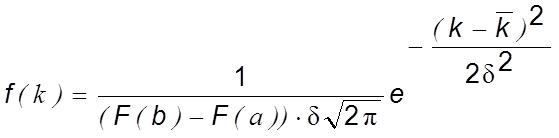Для моделирования разработки нефтяных месторождений используются различные модели нефтяных пластов [1-4]. Очень часто пласты являются неоднородными. Один из видов неоднородного пласта- слоистый пласт [5-6]. Для построения модели неоднородных пластов используются различные законы распределения характеристик пласта. В некоторых месторождениях распределение слоистой неоднородности соответствует нормальному распределению. Целью работы являлось построение модели слоистой неоднорости пласта, которая подчиняется нормальному закону распределения.
Создадим модели слоистого пласта из 5 и 10 пропластков, отличающихся по абсолютной проницаемости.
Данные для пропластков: одинаковая толщина Hj=H/5 и Hj=H/10 (для 5 и 10 слоёв соответственно, H – толщина всего пласта), проницаемость каждого пропластка – Kj.
В работах [7-8] были рассмотрены модели для различных распределений: равномерного, бетта, гамма, Максвелла, экспоненциального.
Зададим дискретное распределение проницаемости пропластков Kj для нормального закона распределения.
Нормальный закон распределения проницаемости задается функцией плотности распределения вероятности (1):
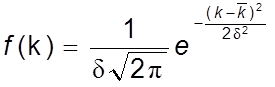 |
(1) |
Для выбранной модели используется усечение распределения, так как значения проницаемости не имеют физического смысла для отрицательной области значений проницаемости. С учетом усечения плотность распределения вероятности примет вид (2):
|
(2) |
Функция распределения усеченного распределения связана с исходным распределением соотношением:
|
(3)
|
где а и b – границы усечения.
Значение параметров нормального распределения зададим такими:
a=0, b=1.8, µ=0.5, δ=0.4 (коэффициент вариации задаем 0.3, так как для нормального распределения он как правило не превышает это число)
При b > 1.8 значение плотности вероятности меньше 0.001 , поэтому взято значение b=1.8
Проницаемость каждого пропластка Kj (j =1…5 для случая 5 пропластков и j =1…10 для случая 10 пропластков) вычисляем по формуле
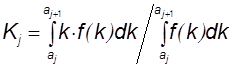 |
(4) |
Алгоритм расчета реализован на языке программирования С.
В результате были получены проницаемости Kj для случая n=5 и n=10.
Таблица 1. Полученные значения проницаемости Kj для случая n=5
| K1 | K2 | K3 | K4 | K5 |
| 0.082 | 0.327 | 0.517 | 0.712 | 0.985 |
Таблица 2 Полученные значения проницаемости Kj для случая n=10
| K1 | K2 | K3 | K4 | K5 | K6 | K7 | K8 | K9 | K10 |
|
0 |
0.159 | 0.276 | 0.377 | 0.471 | 0.564 | 0.66 | 0.765 | 0.892 | 1.077 |
Чтобы проверить полученные дискретные распределения на правильность построения моделей, необходимо вычислить основные параметры распределения (математическое ожидание, коэффициент вариации, дисперсия).
Средние значения проницаемостей для 5 и 10 пропластков равны 0.5, так же, как и для непрерывного распределения.
среднеквадратическое отклонение получили равным 0.3, что незначительно отличается от непрерывного случая.
Для непрерывного усеченного распределения получили близкие значения основных параметров распределения.
Заключение
Из полученных результатов видно, что параметры созданных дискретных моделей близки к аналогичному нормальному распределению. Это показывает, что полученные модели можно использовать для моделирования слоистых неоднородностей в пластах.
Библиографический список
- Плохотников С.П. Методика построения модифицированных относительных фазовых проницаемостей в моделях трехфазной фильтрации в слоистых пластах/Богомолова О.И., Плохотников Д.С., Богомолов В.А., Белова Е.Н., Харина М.В., Низаев Д.Д.//Вестник Казанского технологического университета, 2013, т. 16, № 21, с. 287-289
- Плохотников С.П. Математическое моделирование неизотермической двухфазной фильтрации с модифицированными относительными фазовыми проницаемостями/Богомолова О.И., Плохотников Д.С., Богомолов В.А., Плохотникова О.Р., Нурсубин М.С.//Вестник Казанского технологического университета. -2013. -т. 16. -№ 21. -c. 122-124.
- Плохотников С.П. Осреднение моделей трехфазной фильтрации в неоднородных слоях, подчиняющихся равномерному распределению/Богомолов В.А., Белова Е.Н., Богомолова О.И., Плохотников Д.С., Булгакова О.Р.//Вестник Казанского технологического университета. -2012. -т.15. -№ 1. -с. 63-67.
- Плохотников С.П. Модифицированные ОФП в осредненных моделях фильтрации при закачке в пласт полимерных растворов различной концентрации/Богомолов В.А., Белова Е.Н., Богомолова О.И.//Вестник Казанского технологического университета. -2012.-т. 15.-№ 1. -с.55-58.
- Плохотников С.П. Оценка погрешности двух осредненных моделей при двухфазной неизотермической фильтрации для экспоненциального закона распределения/Плохотников С.П., Богомолова О.И., Белова Е.Н., Богомолов В.А., Низаев Р.Х.//Вестник Казанского технологического университета. -2014. -т. 17. -№ 21. -с. 390-393.
- Плохотников С.П. Осреднение моделей трехфазной фильтрации в неоднородных слоях, подчиняющихся равномерному распределению/Плохотников С.П., Богомолов В.А., Белова Е.Н., Богомолова О.И., Плохотников Д.С., Булгакова О.Р.//Вестник Казанского технологического университета. -2012. -т. 15. -№ 4. -с. 99-102.
- Плохотников С.П.ИССЛЕДОВАНИЕ ВЛИЯНИЯ ФУНКЦИЙ ОТНОСИТЕЛЬНЫХ ПРОНИЦАЕМОСТЕЙ НА ПОГРЕШНОСТИ КАЖДОЙ ИЗ ДВУХ ОСРЕДНЕННЫХ МОДЕЛЕЙ ДВУХФАЗНОЙ НЕИЗОТЕРМИЧЕСКОЙ ФИЛЬТРАЦИИ С ПОМОЩЬЮ ВЫЧИСЛИТЕЛЬНОГО ЭКСПЕРИМЕНТА/Плохотников С.П., Богомолова О.И., Белова Е.Н., Богомолов В.А., Климова А.С. //Вестник Казанского технологического университета. -2015. -т. 18. -№ 20. -с. 198-202.
- Плохотников С.П.СРАВНИТЕЛЬНЫЙ АНАЛИЗ ДВУМЕРНЫХ И ТРЕХМЕРНЫХ ЧИСЛЕННЫХ РЕШЕНИЙ ДЛЯ ДВУХВЕРОЯТНОСТНЫХ ЗАКОНОВ ПРИ ДВУХФАЗНОЙ НЕИЗОТЕРМИЧЕСКОЙ ФИЛЬТРАЦИИ В СЛОИСТЫХ ПЛАСТАХ /Плохотников С.П., Богомолова О.И., Богомолов В.А., Климова А.С., Белова Е.Н. //Вестник Казанского технологического университета. -2015. -т. 18. -№ 20. -с. 210-214.
- Плохотников, С П К вопросу об использовании осредненных моделей для расчета показателей разработки слоистого пласта / С.П.Плохотников, Казан, физ.-тех ин-т, Казан, фил АН СССР // «Вопросы подземной гидромеханики и оптимизации нефтедобычи» – Казань, 1985г 4.1 С. 115-125