Воздушный транспорт является одним из наиболее распространенных способов передвижения на дальние расстояния. В воздухе одновременно может находиться большое количество самолетов, поэтому следует контролировать и при необходимости корректировать их маршрут, высоту и скорость. Такие мероприятия выполняет система управления воздушного движения (СУВД).
Важным элементом в управлении воздушным движением является определение координат воздушного судна. Эта задача может выполняться, в частности, на основе разностно-дальномерного способа определения координат (РДС). Сущность способа заключается в приеме сигнала с воздушного судна на несколько наземных станций и определение временных задержек, по которым и определяются координаты судна в пространстве.
Разработка разностно-дальномерного алгоритма является весьма значимой для управления воздушным движением, так как его внедрение позволяет с достаточной точностью определять координаты воздушного судна, а, следовательно, предупреждать столкновения воздушных судов между собой и с другими препятствиями, что могло бы повлечь заметный ущерб.
В воздушном пространстве имеется объект, стоит задача определить его местоположение. Модель изображена на рис. 1
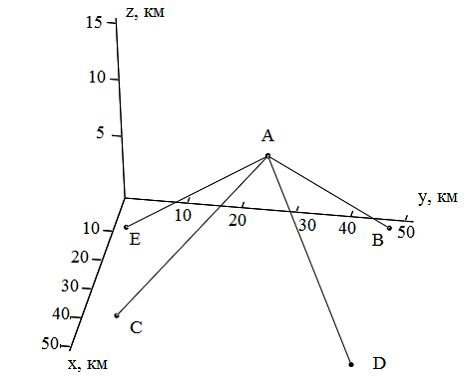
На рис. 1 точкой А обозначен объект, точки B, C, D, E – наземные локаторы. Проведем расчет расстояний от самолета до каждого из радиолокаторов (1).
Далее находим время прихода сигнала от самолета к радиолокатору по формуле
где с – скорость распространения сигнала (с = 300000 км/с).
Рассчитаем временные задержки относительно прихода сигнала на радиолокатор B по формуле
где t – время прихода сигнала на радиолокаторы C, D и Е.
Задача состоит в определении координат по временным задержкам. Допустим, что имеется примерное местоположение объекта, то есть область, в пределах которой он находится. Проводится разбиение области с некоторым шагом, проводится расчет набора временных задержек для каждой возможной точки местоположения объекта.
Когда все временные задержки вычислены, проводится вычисление суммы квадратов разностей временных задержек: из каждого элемента матрицы временных задержек вычитается заданная временная задержка, результат возводится в квадрат. Затем вычисляется сумма матриц квадратов разностей:
где ![]()
![]() – заданные временные задержки;
– заданные временные задержки;
![]()
![]() ,
, ![]()
![]() – рассчитанные матрицы временных задержек. Минимальной сумме квадратов разностей будет соответствовать наиболее точное местоположение объекта.
– рассчитанные матрицы временных задержек. Минимальной сумме квадратов разностей будет соответствовать наиболее точное местоположение объекта.
Далее представляется интересным выяснить влияние различных шумов, присутствующих в реальной среде, на точность определения координат. Рассмотрим влияние аддитивного шума, при котором временные задержки будут отличаться на случайные величины, заданные нормальным распределением. Изменяя среднеквадратическое отклонение случайной величины нормального распределения, рассматриваем погрешности определения координат. Для случая, когда объект находится внутри объекта (рис. 1), построим график зависимости погрешности координат от среднеквадратического отклонения случайной шумовой поправки. График приведен на рис. 2
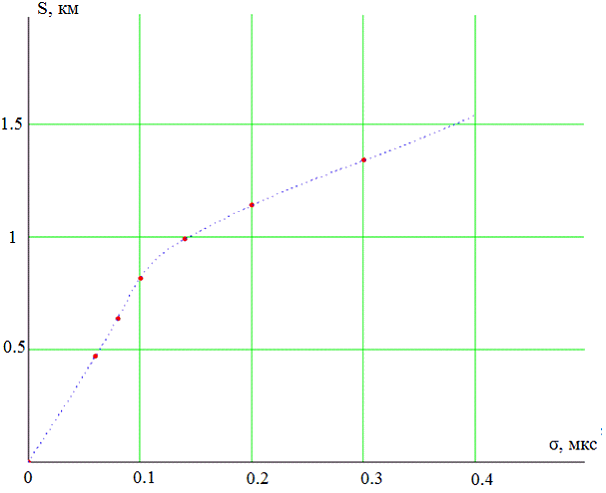
По рис. 2 делаем вывод, что отклонение временных задержек на 0.14 мкс способно вызвать погрешность в определении координат практически на 1 км. Если принять за допустимую погрешность определения координат 300 м, то делаем вывод, что в ситуации, когда самолет находится внутри системы, допускается отклонение временных задержек примерно на 0.04 мкс.
Рассмотрим другие случаи расположения объекта относительно разностно-дальномерной системы. Для случая нахождения объекта на краю системы (рис. 3) построен аналогичный график, он представлен на рис. 4
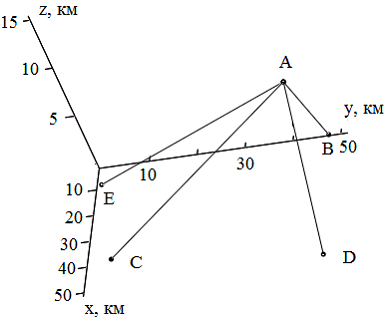
В случае, когда самолет находится на краю системы, допускается поправка во временных задержках порядка 0.05 мкс, что соответствует 300 м погрешности в определении координат.
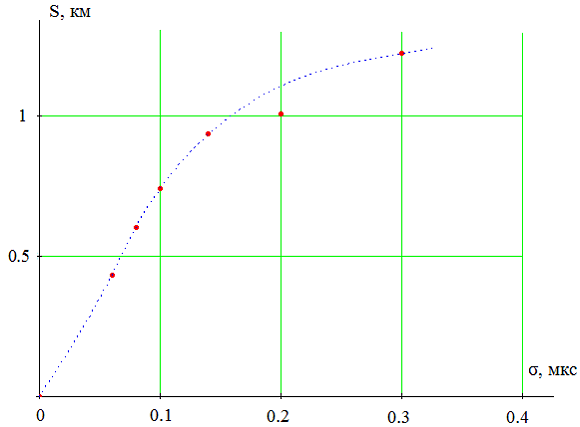
Проведем исследование для нахождения местоположения объекта за пределами системы радиолокаторов. Модель показана на рис. 5, график зависимости погрешности координат от среднеквадратического отклонения случайной шумовой поправки приведен на рис. 6
Следует заметить, что погрешности определения координат даже при небольших среднеквадратических отклонениях случайных поправок довольно высоки. Для того, чтобы погрешность определения координат не превысила 300 м, необходимо, чтобы отклонение временных задержек не была больше 0.02 мкс в случае с самолетом, находящимся на пределами рассматриваемой системы.
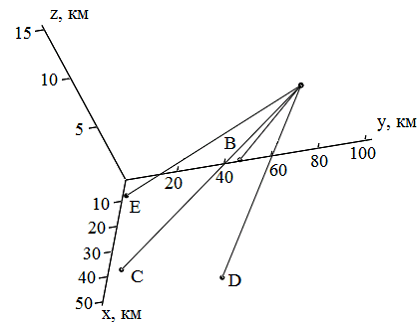
Рисунок 5
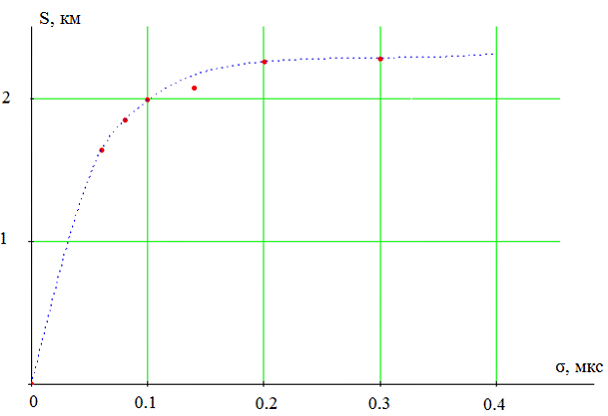
Рисунок 6
Рассмотрим частные случаи, когда направления путей прохождения сигнала от двух радиолокаторов лежат на одной прямой, если рассматривать относительно плоскости xy. Наглядно эти случаи показаны на рис. 7-8.
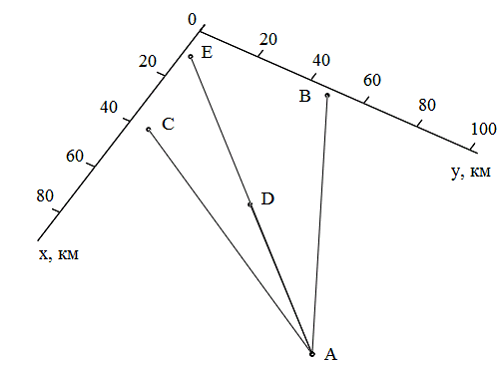
Рисунок 7
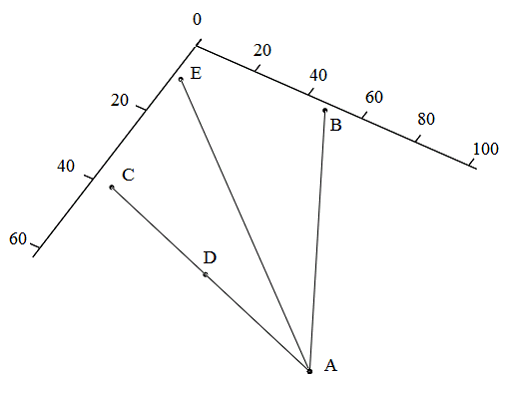
Рисунок 8
Рассмотрим первый частный случай (рис. 7). Его график зависимости погрешности от СКО приведен на рис. 9
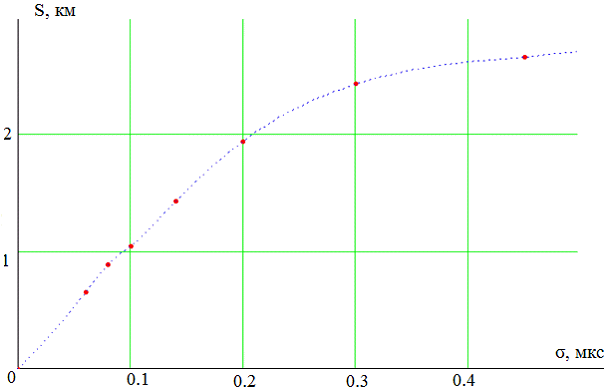
По рис. 9 видно, что в случаях нахождения направлений сигнала на одной прямой погрешность в определении координат довольно высока: около 300 м при 0.03 мкс.
График для второго частного случая приведен на рис. 10. Видно, что для погрешности порядка километра будет достаточно более 0.1 мкс. В нашем случае допустимой погрешностью считаем примерно 300 м, такой погрешности можно достигнуть, если во временной задержке будет неточность порядка 0.025 мкс.
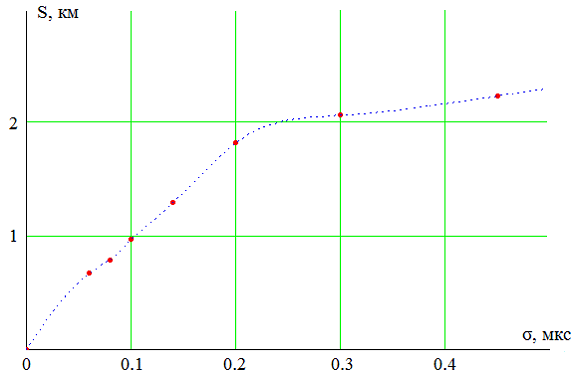
Рисунок 10
Таким образом, в реальных условиях на определение координат с достаточной точностью влияет не только шумовая компонента, но и расположение объекта относительно системы радиолокаторов.
Блок-схема алгоритма обработки сигналов представлена на рис. 11
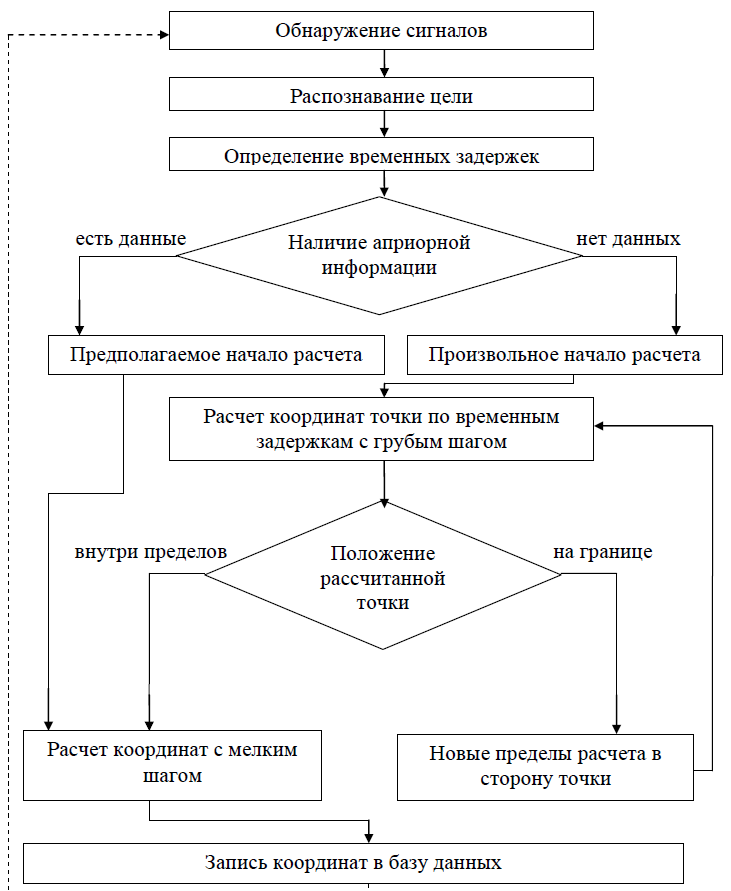
Рисунок 11
Рассмотрим каждый из этапов обработки сигналов подробнее:
1) обнаружение сигналов состоит в обнаружении преамбулы. Для нахождения преамбулы используется функция взаимной корреляции между принятым и опорным сигналом;
2) распознавание цели – декодирование информации о номере борта самолета. Для гражданских воздушных судов используется прямое декодирование, для военных – косвенное (по уровню сигнала);
3) определение временных задержек производится измерением времен момента прихода сигнала на радиолокаторы. Измерение времен моментов прихода можно произвести с помощью алгоритма взаимной корреляционной обработки принятых сигналов. Реализация разностно-дальномерного метода требует наличия шкалы единого времени во всех пунктах системы;
4) наличие априорной информации – стадия, в которой выясняется, существуют ли априорные данные о курсе и скорости движения воздушного судна. Если данных нет, то для расчета выбирается произвольная область. В ином случае будет использоваться приближенное положение самолета, которое будет принято за центр расчета и расчет возможен далее с мелким шагом;
5) расчет с грубым шагом – выбираются пределы на основе предыдущего пункта, проводится расчет координат с грубым шагом;
6) положение рассчитанной точки в результате грубого расчета находится либо внутри системы, либо на краю системы. Тогда принимается решение: при нахождении внутри системы выполняется расчет с мелким шагом, если рассчитанная точка на краю – провести итерацию в сторону нахождения точки. Рассмотрим подробнее этот процесс. На рис. 12 обозначены радиолокаторы и цель, представленная самолетом. Пунктир на графике представляет собой границы расчета. Точка А имеет координаты (20, 34, 10), пределы расчета – 17…23 по x, 27…33 по y, 7…13 по z.
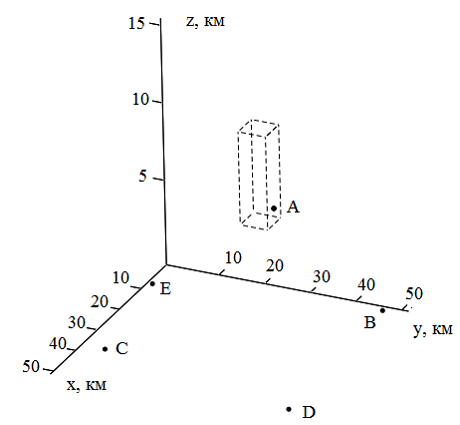
Как видно по рис. 12, точка А оказалась на границе расчета – грани параллелепипеда. Видно, что точка находится на грани, соответствующей оси у, следовательно, произведем расчет с новыми пределами по оси у. Зададим пределы расчета по оси у 32…38. Результат нового расчета координат точки представлен на рис. 13. На нем видно, что точка вошла в предел расчета, следовательно, полученный расчет точки будет верным. Следует отметить, что расчет выполнен в две итерации, но в разных ситуациях количество итераций может меняться. Для выполнения меньшего количества итераций следует увеличить пределы расчета при увеличении шага расчета.
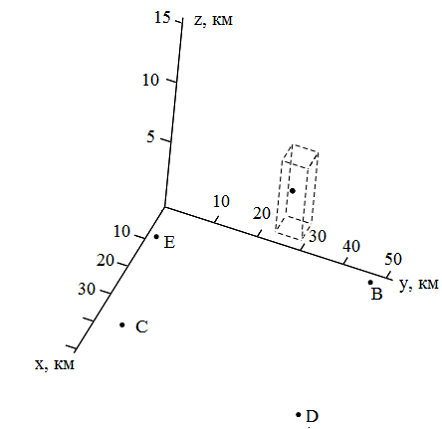
Рисунок 13
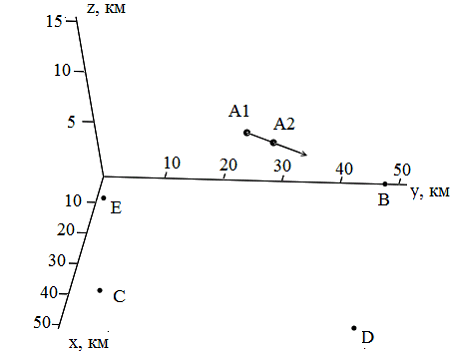
7) Запись в базу данных – координаты записываются в базу данных с соответствующим текущим моментом времени. Записанные координаты впоследствии могут использоваться для предсказания будущих координат. Пример указан на рис. 14.
На рис. 14 показана система координат, в которой присутствуют радиолокаторы, а также две точки: А1 – точка, занесенная в базу данных координат, А2 – новая рассчитанная точка. Стрелкой указано дальнейшее предполагаемое направление движения. Его вероятность наиболее высока при прямолинейном равномерном движении. Далее возможно определить примерные пределы расчета и рассчитать точку с мелким шагом, минуя пункт грубого шага. После записи в базу данных выполняется следующее вычисление координат, так как цель не «висит» на одном месте в воздухе и передвигается.
Хотя представленный выше алгоритм и не является оптимальным, его преимуществом является простота, обуславливающая целесообразность его практического использования.
Представленный в работе разностно-дальномерной алгоритм оценки координат воздушных судов предусматривает поиск минимума расхождений расчетных и экспериментально полученных взаимных задержек сигналов на сетке контрольных точек, шаг между которыми подбирается адаптивно.
Разработанная модель процесса оценки координат воздушного судна по временным задержкам показала работоспособность предложенного алгоритма и позволила провести исследование влияния шумовой компоненты на точность определения координат. Аддитивный шум влияет на величину временных задержек, а, следовательно, на точность определения координат воздушных судов разностно-дальномерным методом. Для определения координат с точностью не хуже 300 метров среднеквадратической погрешности максимально допустимое отклонение измеренных временных задержек от идеальных (теоретических) должно составлять не более 0.03 мкс.
Библиографический список
- Пат. РФ 2363010, разностно-дальномерный способ определения координат и реализующее его устройство / А. Г. Сайбель, К. И. Вайгель, М. И. Михайлов. – Санкт-Петербург: Военно-космическая академия имени А. Ф. Можайского, 2009. – 16 с.
- Руководство по вторичным обзорным ВОРЛ системам: издание третье / международная организация гражданской авиации, 2004. – 254 с.
- Прием и декодирование данных системы управления воздушным движением ADS-B / Хе Лиюань, М. Л. Усс. – Харьков: Национальный аэрокосмический университет им. Н. Е. Жуковского, 2014. – 4 с.
