1. Introduction
Natural gas has become an important resource of energy since it has low environmental impact. Currently, 70 percent of gas is transported to market by pipeline and 30 percent as liquefied natural gas (LNG). Pipelines are attractive even offshore, but require huge upfront investments. LNG onshore facilities are expensive to build and the dual production process (liquefaction and regasification) is costly and energy wasteful. Marine transport of compressed natural gas (CNG) can be a successful alternative thus allowing upstream oil & gas companies to monetize gas reserves that otherwise would remain stranded. The prospective regions like the entire Mediterranean basin, the Scandinavian peninsula, Sakhalin Island, South-East Asia and the would be better served by CNG even if LNG projects have already been approved and under construction. Satisfying small markets and monetizing small reserves are the two main targets that CNG schemes intend to pursue. This would unlock reserves, which otherwise, would remain stranded and would supply many small markets that couldn’t be economically justified via pipeline or LNG. The scalability of the CNG sea transport system and the opportunity to reuse its major assets (the carrier vessels) make this concept even more attractive (Wagner et al, 2002). [5]
The criterion selected for the assessment of the economic desirability of CNG and LNG sea transport projects is the Net Present Value (NPV). A comprehensive calculation model has been developed that, staring from a hypothetical market demand of natural gas located at a certain distance from a source, determines the optimal configuration for the transportation scheme (optimal number of vessels with a given size) and then determines the discounted cash flow as the difference between the generated annual revenue stream and the tailored outlay of capital and operating costs. By comparing full project life conclusions from expected NPVs can be drawn about the profitability of the transporting option (CNG versus LNG) as well as the specific configuration for the transportation schemes.
2. Background information about Sakhalin Island
Sakhalin Island is located off Russia’s eastern shore with recoverable oil reserves around 7 billion barrels, and natural gas reserves at approximately 2200 Bcm (80 Tcf). [7].
According to the Sakhalin Energy Investment Company LTD, Sakhalin 1 has three energy fields : Chayvo, Odoptu and Arkutun Dagi. These three fields with natural gas resources estimated at 17 trillion cubic feet (485 billion cubic meters, Sakhalin 1 website), can provide a large long-term commercial supply of gas for export and regional domestic supplies in Russia.
Sakhalin II comprises two fields in the sea of Okhotsk offshore Sakhalin Island: The Piltun-Astokhskoe field which is primarily an oil field with some associated gas and the Lunskoe field which has large reserves of gas and some oil. The two fields contain reserves of approximately 140 million tons (1 billion barrels) oil and 550 Bcm (20 Tcf) natural gas. [6]
LNG transportation from these Islands to Japan, Korea and china is already in progress, but it’s not the best option from an economic point of view. It is far more attractive to transport CNG from Sakhalin Island to North-East Asia because the distances from the source (Sakhalin Island) to the markets (Japan, Korea and China) are in the range of 1,500 to 3000 km (about 900 to 1800 miles). The current pipeline and LNG network of Sakhalin is shown in figure below.
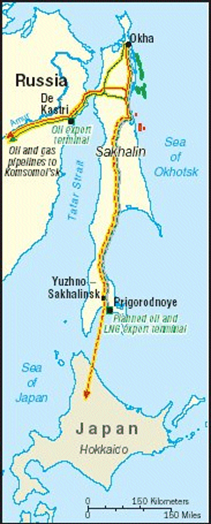
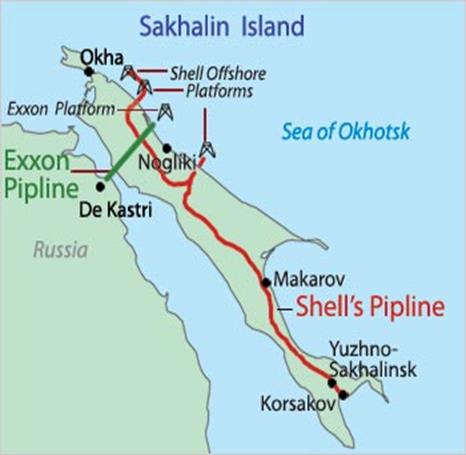
Figure 1: Natural gas supply network of Sakhalin Island
3. Case Study
The parameters used to compare CNG and LNG transportation of Sakhalin Island are as follows:
Distance
The distance from source (Yuzhno-Sakhalinsk) to consumers Japan, China and Korea is as follows:
-
Sakhalin à Sapporo, Japan ~ 500 km
-
Sakhalin à Tokyo, Japan ~ 1500 km
-
Sakhalin à Seoul, S. Korea ~ 2600 km
-
Sakhalin à Shanghai, China ~ 2600 km
Gas demands
-
Sapporo ~ 2 Bcm/year
-
Tokyo ~ 2 Bcm/year
-
Seoul ~ 1 Bcm/year
-
Shanghai ~ 2 Bcm/year
The constant gas consumption rate is assumed. Another important assumption is that, the receiving terminal is not equipped with any temporary storage facility (neither land nor offshore). This means that once the vessels are moored and connected to the offloading system, gas will be fed directly to the final destination point, at an offloading rate equal to the required consumption rate. The optimal number of vessels needed is determined as a direct function of the following parameters:
-
Vessel capacity;
-
Vessel sailing speed;
-
Transit distance between source and final destination;
-
Gas loading rate (the offloading rate is assumed to be the same as the required consumption rate);
-
Connecting and disconnecting times to the loading/unloading systems. [3]
4. Hub and Spoke Distribution Pattern
To determine the values of above mentioned parameters, we use the Hub-and-Spoke distribution pattern as the gas demand rate is relatively higher. As it has been demonstrated (Nikolaou, 2010), the minimum capacity required to a CNG ship to transport natural compressed gas for given maximum loading and offloading rates is determined as:
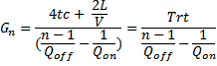 (1) - [2]
(1) - [2]
Where,
tc = connecting/disconnecting time (h)
L = distance from source to receiving site (nm)
V = ship service speed (kn)
Qoff = maximum offloading rate (mmscf/h)
Qon = maximum loading rate (mmscf/h)
and where Trt = 4Tc + L/V denotes the total round-trip time from delivery site to the source and back after gas loading plus the total time for connecting/disconnecting the ship to/from the buoys.
To determine the minimum capacity of a fleet organized in m trains each of n ships:
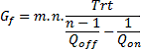 (2) - [2]
(2) - [2]
It can be demonstrated that the fleet capacity is bounded by a lower and an upper limit, respectively, depending on the gas consumption rate, Qu, which can be actually absorbed by destination terminals:
![]() (3) - [2]
(3) - [2]
assuming that the offloading rate equals the daily absorption at gas by each terminal, e.g. Qu = Qoff
Figure 2 provides the required fleet capacity and its lower and upper bounds, Ll and Lu, respectively, with parameters tc = 1.5 h, V = 18 kn, and Qoff = Qon, while considering one, two and three trains of ships, e.g. m = 1, 2, 3.
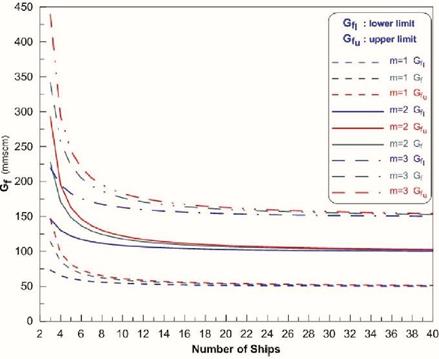
Figure 2: Gf and its bounds in terms of number of ships and trains
It can be easily seen that increasing number of ships causes that the limit lines bounding Gf approach each other until they coincide as a large number of smaller ships are employed at a capacity value given as:
![]() (4) - [2]
(4) - [2]
Some preliminary conclusions may be drawn from parametric analysis of the above formulae which serve an order-of-magnitude assessment of minimum fleet capacity. The necessitated CNG fleet capacity substantially depends on the distance to ship speed ratio (L / V) and consumption rate Qu /Qoff.
5. Bounding Ship Capacity in Fleet Composition
Capacity of CNG ships as well as their loading/offloading rates stays within certain limits because of technical and economic reasons. On the lower side, even with very low consumption rate and storage facility the tariff would not be competitive with subsea pipelines. On the upper side, the initial investment would be too high; moreover, to avoid too long loading/offloading times would require very large, heavy and expensive compressors on board.
When the CNG marine transport adopts the hub-and-spoke model, the first activity is to select the ship capacity as a function of consumption rate, Qu. Initially, consider a fleet of two ships. When the minimum capacity value G2 overtakes the upper bound that a CNG ship may reach in a single distribution train due to technical limits and economic inconvenience, it would be necessary to assess G3, then eventually G4, and so forth, until ship size will be within technical and building standards. On the contrary, would G2 be lower than minimal feasible capacity, it shall be advisable to plan the fleet following the milk-run model.
To clarify the matter, suppose a shipping company is asked to transport gas loaded at 12 MMscm/d and supplied to three distinct receiving points through the hub-and-spoke mode. The ships’ service speed is settled at 18 knots. The minimal capacities and related bounds required by the three corresponding fleets with varying number of ships (2 ≤ n ≤ 6) are given as a function of consumption rate at receiving location in the technical-logistic separation diagram below:
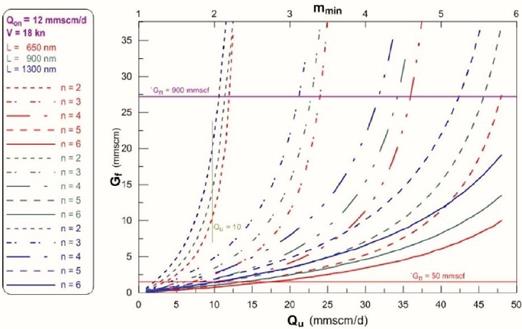
Figure 3: Gf and its bounds in terms of consumption rate for given number of ships in the fleet
The two horizontal lines define the feasible design capacity space. The “best possible” fleet will be decided within the capacity space on the basis of secondary-level criteria, mainly of economic nature. Points below the red horizontal line identify unfeasible solutions where the hub-and-spoke approach would led to wasting of ship capacities; points above the purple horizontal line identify insufficient overall capacity of a fleet to satisfy consumption demand. The design capacity space offers a number of feasible solutions. However, as it will be demonstrated later, searching for minimum transport tariff will lead to trains with the lower possible number of medium-sized ships.
Each vessel is required to continuously iterate the cycle of loading and offloading at the source and market, in a perfectly synchronized schedule with the other vessels employed. The minimum required number of vessels is set to be three.
Gas thermal content ratio is set at 1040 BTU/scf, gas price at source is set at $8/MMBtu, gas selling price is set at $16/MMBtu and discount rate is set at 15%.
Based on these assumptions, NPV is calculated for 15 years, capital expenditures are invested at time zero.
6. Economic analysis of CNG and LNG projects
Customers at the final destination want to pay as little as possible for the delivered loads of either CNG or LNG, while the initial gas providers want to sell gas at the highest possible price. Therefore, the potential CNG/LNG project operators have to establish long term agreements (generally linked to the project timeframe) with both gas providers and customers at the final destination and try to achieve their maximum profit. They need to identify the breakeven point at the given difference between the two gas prices (source and destination). [9]
At the discount rate of 15%, the resulting breakeven selling gas price at the market for CNG and LNG are calculated for a range of buying prices at the source. The gas transported as CNG can be sold at considerably lower prices than gas transported as LNG. For example, if the source price is $6, the prices for CNG would be 10.05 whereas for LNG would be 14.24. That is almost 40% higher. The detailed input values are given below.
Input values for CNG study
| Gas supply needed, Bcm/year |
1.5 |
| Transit distance |
1500 |
| Sailing Speed |
14 |
| Vessel Capacity, MMscf |
150 |
| Number of vessels |
7 |
| Fuel usage |
5% |
| CAPEX per vessel |
$ 115 000,000 |
| CAPEX loading facility |
$ 50 000, 000 |
| CAPEX offloading facility |
$ 25 000, 000 |
| Crew daily cost |
$ 5 000 |
| Annual Maintenance |
2% |
| OPEX contingency |
10% |
| Insurance |
0.8% |
| Project life, year |
15 |
| CPI |
2.5% |
| Discount rate |
15% |
| Taxes |
35% |
Table 1: CNG input data
Input values for LNG study
| Gas supply needed, Bcm/year |
1.5 |
| Transit distance |
1500 |
| Sailing Speed |
14 |
| Vessel Capacity, MMscf |
3000 |
| Number of vessels |
3 |
| Fuel usage |
7% |
| LNG thermal efficiency |
78% |
| CAPEX per vessel |
$ 150 000,000 |
| CAPEX liquefaction facility |
$ 500 000, 000 |
| CAPEX regasification facility |
$ 400 000, 000 |
| Utilities & Offsite |
$ 80 000, 000 |
| Crew daily cost |
$ 15, 000 |
| Annual Maintenance |
5% |
| OPEX contingency |
12% |
| Insurance |
1% |
| Project life, year |
15 |
| CPI |
2.5% |
| Discount rate |
15% |
| Taxes |
35% |
Table 2: LNG input data
The tables above show the allowable gas price at the source for a given sale price at the destination. For $15 sale price, gas for LNG should be purchased at no more than $7 whereas gas intended for CNG can be purchased almost at $11 and still be economically attractive. [8]
The graphical illustration of CNG and LNG projects is shown below in figure 4.
Figure 4: Capital cost calculation of CNG and LNG projects
7. Concluding remarks of study case
As expected, at low gas demand and a relative short distance, LNG simply cannot compete with CNG even at distance of 3000 km. Results show that, at gas demand of 1 Bcm/year, the NPV of CNG is $ 1,723 million at 500 km and 473 million at 3000 km. At 2 Bcm/year, the NPV is $ 767 million at 500 km and $85 million at 3000 km. LNG, on the other hand significantly, underperforms. The NPV is negative $627 at 1 Bcm/year and $168 million/year at 2 Bcm/year within 3000 km.
The number of vessels needed for CNG is calculated based on database of CNG ships. The number of vessels needed for CNG is much bigger than three but CNG is much attractive than LNG to transport natural gas from Sakhalin to Sapporo, Tokyo, Shanghai and Taipei, if the gas demand is within 2 Bcm/year. For a given buying price at the source, gas transported as CNG can sell at about 40% lower price at the destination than gas transported as LNG.
References
- Wood D., Mokhatab, S., Economides, M.J., 2008. Technology options for securing markets for remote gas. In: 87th Annual Convention, GPA, Grapevine TX.
- Nikolaou, M., Economides, M.J., Wang, X., Marongiu-Porcu, M.: Distributed Compressed Gas Sea Transport, Proceedings of the 2009 Offshore Technology Conference, Houston, OTC 19738, 2009, pp. 1-14.
- Santi, F.: Nimby-Proof Marine Transport of Gas (in Italian), in Nuova Energia, no. 4, 2007.
- XGAS LLC (http://www.xgas.us)
- Sea NG Corporation (http://www.coselle.com)
- Sakhalin-I project (http://www.sakhalin1.com)
- IHS Energy (http://www.energy.ihs.com)
- Gas Technology Institute (http://www.gastechnology.org)
- Enersea Transport LLc (http://www.enerseatransport.com)
- Energy Information Administration, department of energy (http://www.eia.doe.gov)
