В работе исследованы две краевые задачи для уравнения смешанного типа
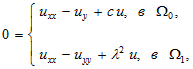 (1)
(1)где ![]() – область ограниченная отрезками АВ, ВС, СО и ОА прямых
– область ограниченная отрезками АВ, ВС, СО и ОА прямых ![]() ,
, ![]() ,
, ![]() ,
, ![]() соответственно;
соответственно; ![]() – характеристический треугольник, ограниченный отрезком ОА оси абсцисс и двумя характеристиками АD:
– характеристический треугольник, ограниченный отрезком ОА оси абсцисс и двумя характеристиками АD: ![]() , ОD:
, ОD: ![]() уравнения (1), выходящими из точек А, О и пересекающимися в точке D;
уравнения (1), выходящими из точек А, О и пересекающимися в точке D; ![]() и
и ![]() – заданные коэффициенты,
– заданные коэффициенты, ![]() ;
; ![]() .
.
Задача 1. Найти регулярное в ![]() ,
, ![]() , решение уравнения (1) из класса
, решение уравнения (1) из класса ![]() , удовлетворяющее краевым условиям
, удовлетворяющее краевым условиям ![]() ,
,
и условиям сопряжения:
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , причем
, причем ![]() .
.
Задача 2. Найти функцию ![]() , удовлетворяющую всем условиям задачи 1, кроме условия (5), которое заменено условием
, удовлетворяющую всем условиям задачи 1, кроме условия (5), которое заменено условием
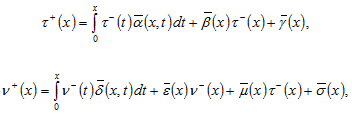
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() , причем
, причем ![]() .
.
На отрезке АО имеем функциональное соотношение принесенное из области ![]()
Соотношение же между ![]() и
и ![]() , принесенное на отрезок АО из гиперболической части
, принесенное на отрезок АО из гиперболической части ![]() смешанной области
смешанной области ![]() легко получить выписав решение соответствующей задачи Коши, а затем удовлетворив его краевому условию (3). В результате этих преобразований, находим
легко получить выписав решение соответствующей задачи Коши, а затем удовлетворив его краевому условию (3). В результате этих преобразований, находим
где
Подставляя ![]() из первого уравнения условий (4) во второе, получим
из первого уравнения условий (4) во второе, получим
или
где
Отсюда, с учетом (5), следует, что
Теперь, подставляя ![]() из первого уравнения условий (4) в соотношение (6), будем иметь
из первого уравнения условий (4) в соотношение (6), будем иметь
или
где
Обращая интегральное уравнение Вольтерра второго рода (8) через резольвенту ![]() ядра
ядра ![]() , получим
, получим
или
где
Подставляя равенство (9) в соотношение (7), будем иметь
Отсюда, в результате ряда элементарных преобразований, получим
Полагая здесь
приходим к равенству
Интегрируя полученное равенство, будем иметь
Меняя порядок интегрирования в третьем слагаемом последнего равенства, получим
или
где
Интегрируя равенство (10), будем иметь
Вновь меняя порядок интегрирования, но теперь, во втором слагаемом, приходим к следующему интегральному уравнению Вольтерра второго рода относительно функции ![]() :
:
где
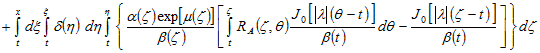 ,
,.gif) .
.Заметим, что ![]() зависит от двух неизвестных постоянных
зависит от двух неизвестных постоянных ![]() ,
, ![]() , первая из которых легко находится из условия (2). В самом деле, из этого равенства, имеем
, первая из которых легко находится из условия (2). В самом деле, из этого равенства, имеем ![]() .
.
Теперь, обращая интегральное уравнение (10), через резольвенту ![]() ядра
ядра ![]() , будем иметь
, будем иметь
Очевидно, что функция ![]() представима в виде
представима в виде
где
.gif) .
.Отсюда, с учетом (11), будем иметь
Полагая в этом равенстве ![]() , получим
, получим
Таким образом, отсюда находим искомую постоянную ![]() , при условии, что
, при условии, что ![]() . Тогда, функция
. Тогда, функция ![]() однозначно определяется равенством (11), функции же
однозначно определяется равенством (11), функции же ![]() находятся из соотношения (9), а
находятся из соотношения (9), а ![]() – из условий сопряжения (4). Теперь, очевидно, что решение задачи 1, легко найти как решение соответствующей задачи Коши в области
– из условий сопряжения (4). Теперь, очевидно, что решение задачи 1, легко найти как решение соответствующей задачи Коши в области ![]() и первой краевой задачи в области
и первой краевой задачи в области ![]() , для уравнения (1).
, для уравнения (1).
В заключении отметим, что условие ![]() в задаче 1 не является необходимым, так как при его нарушении, условия (4), как легко заметить, представляют собой частный случай условий сопряжения задачи 2, которая исследуется аналогично задаче 1.
в задаче 1 не является необходимым, так как при его нарушении, условия (4), как легко заметить, представляют собой частный случай условий сопряжения задачи 2, которая исследуется аналогично задаче 1.
Библиографический список
- Елеев В.А., Лесев В.Н. Задачи со смещением для вырождающихся гиперболических и смешанных уравнений. Конспект лекций. – Нальчик: Каб.-Балк. ун-т, 2003. – 109 с.
- Желдашева А.О., Лесев В.Н. Краевая задача для смешанного уравнения в ограниченной области // Фундаментальные исследования. 2015. №9-3. С. 460-463.
- Лесев В.Н. Нелокальные краевые задачи для смешанных уравнений с негладкими линиями изменения типа. Диссертация на соискание ученой степени кандидата физико-математических наук. Нальчик, 2003.
- Лесев В.Н., Желдашева А.О. Неклассическая краевая задача для смешанного уравнения второго порядка с интегральными условиями сопряжения // Известия Смоленского государственного университета. 2013. № 3 (23). – С. 379-386.
- Лесев В.Н., Желдашева А.О. Нелокальная краевая задача для уравнения смешанного типа второго порядка в характеристической области // Вестник Адыгейского государственного университета. Серия 4: Естественно-математические и технические науки, 2012. – № 3 (106). – С. 52-56.
- Лесев В.Н., Кодзоков А.Х., Бжеумихова О.И., Карова Ф.А. Локальные и нелокальные краевые задачи для уравнений смешанного типа. Конспект лекций. Учебное пособие. – Нальчик: Каб.-Балк. ун-т, 2014. – 110 с.
