Results and Conclusion
The values of temperature at upper and lower border are accepted equal Tc = 1400 K, Th = 2400 K. The extent of area on an axis х is accepted equal 3000 km, and on an axis y – 1000 km. Lithosphere thickness Ln - 100 km. The Temperatures of solid state Ts and liquid state TL are 1800К and 1900К accordingly. Velocity of movement of a continental plate Uк = 2 сm/year, and velocity of oceanic plate U0 1 сm/year. Re=1,0510-19; Gr= 3,210-14; Pe = 251; Ste = 3. Gravitational acceleration value g = 9,8 is constant.
In fig. 1 the results of calculation for velocity of movement oceanic plate 1 сm/year and angle of a feat under continental plate 30o are submitted.


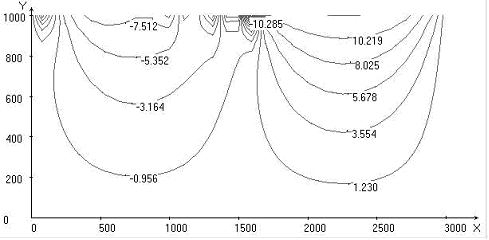
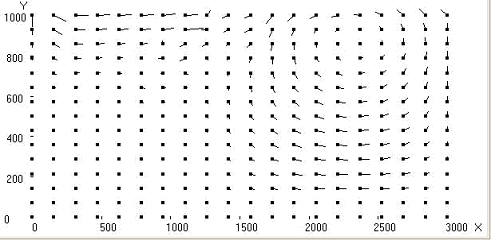
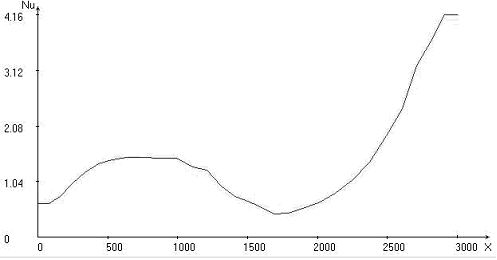
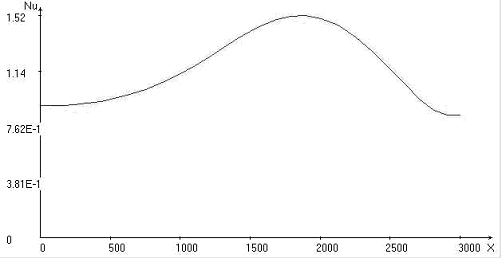
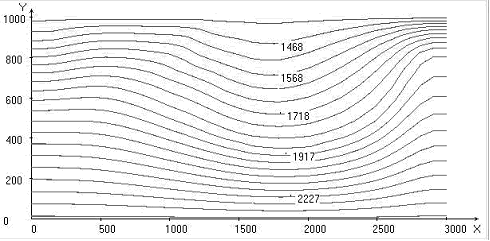
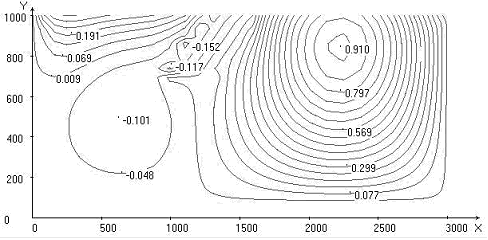
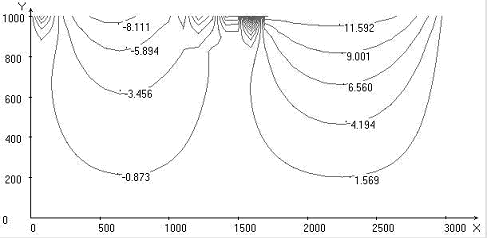
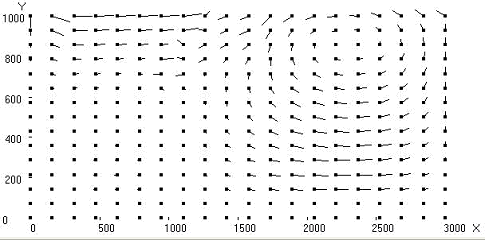
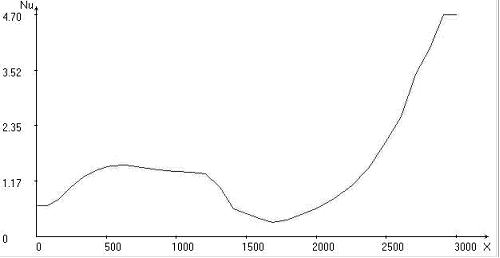
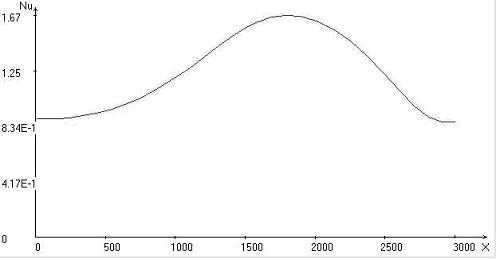
Fig. 1. Calculated fields for = 30o, Uo = 1: temperature; stream function; vortex intensity; velocity vector field; Nusselt number distribution on upper and lower boundaries of the area
In trench region isothermals “bend” to lower boundary of the area. Under oceanic and continental plates two large-scale convective cells are formed, the liquid in which is gone in opposite directions. And besides convective cell and vortex under continental plate flow round immersed lithosphere and penetrate into area of oceanic convective cell and vortex, located to the right of subduction zone, moving them to the right. Immersion depth of the lithosphere reaches about 300 km. The distributions of Nusselt numbers on the upper and lower boundaries of the area are given. At value x ~ 1700 km in the collision region of plates takes place minimum heat flow on the upper border of calculated area that will be agreed with known experimental data [1, 2].
In fig. 2 the results of calculation for velocity of movement oceanic plate 1 сm/year and angle of a feat under continental plate 45o are submitted.
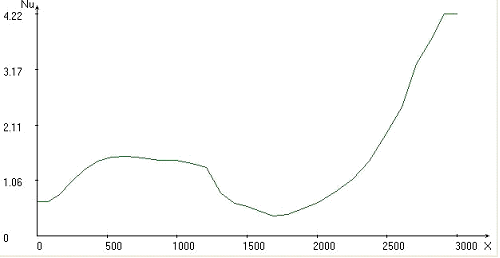
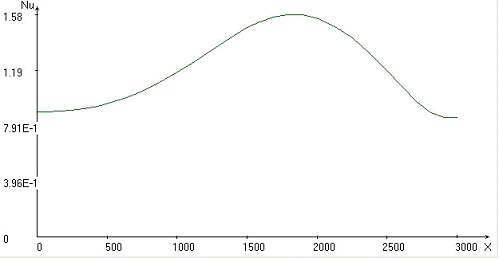
In fig. 3 the results of calculation for velocity of movement oceanic plate 1 сm/year and angle of a feat under continental plate 60o are submitted.
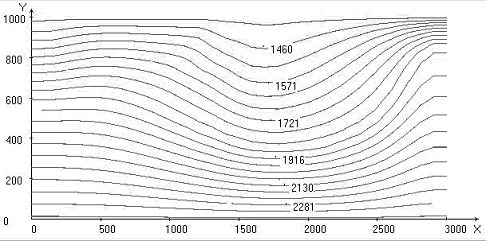

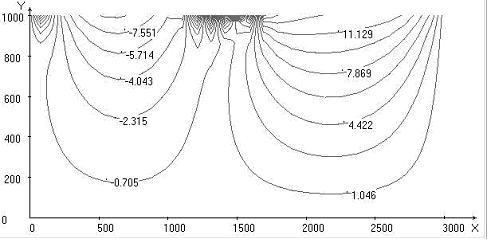
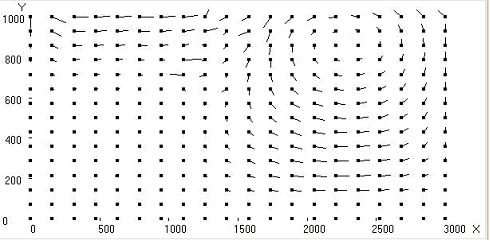
Comparing the results shown in fig. 1, 2, 3, we can see that the immersion depth of lithospheric plate for Uк = 2 сm/year and U0 = 1 сm/year is weakly dependent from the angle of immersing of oceanic plate. With increasing angle of immersing the isotherms deflection in the chute region increases (figs. 1, 2, 3).
The intensity of the stream functions as for cell continental and oceanic increases with increasing angle of immersing. For want of it has a place a small decrease in the continental scale cells and a small increase in the scale of the oceanic cell.
The intensity of the vortex as for a continental cell and oceanic cell will increase, with increasing angle of immersing from 300 to 450 (figs. 1, 2). For the angle 600 (fig. 2) the intensity of the vortex as for a continental cell and oceanic cell decreases on a comparison with the results shown in fig. 3. For all modes scale of continental vortex is decreases and scale of oceanic vortex is increases.
The interval of a modification of significance of the Nusselt number on the upper and lower boundary of the computational domain increases with increasing angle. Minimum heat exchange at the upper boundary of the computational domain and a maximum heat exchange at the lower boundary of the computational domain are at the value of x 1700 km.
In fig. 4 the structure of current of a liquid in a subduction zone for various angle values of subsidence of lithosphere is given. Velocity of movement of a continental plate Uk = 2 сm/year.

Analyzing the results of modeling we can make the following conclusion:
- with the increasing angle of immersing deflection of isotherms in the chute region is increased;
- with the increasing angle of immersing the intensity of a stream function is increased. Scale of a continental cell decreases, and oceanic – increases;
- the intensity of vortex increases with increasing angle of immersing from 300 to 450, and for angle of immersing 600 decreases on a comparison with results for angle 450. For all modes scale of a continental vortex decreases, and oceanic – is increased;
- with the increasing of immersing angle the values of the Nusselt numbers will increase;
- the received decisions as it is qualitative, and will quantitatively be agreed on depth of immersing of a plate in a mantle and under the law of change of a heat flow on a surface of the Earth with known experimental and theoretical results of other authors.Thus, suggested the mathematical model and the results obtained contribute to the available information on investigation of convection in the Earth’s interior and may be of use for better understanding and explanation of such phenomena as subduction, lithospheric plate motion and heat flow change at Earth’s surface.
Библиографический список
- Zharkov, V. N., Trubitsyn, V. P. and Samsonenko, L. V. [1971], Physics of the Earth and planets. Figures and inner structure. Moscow: Nauka, Chief editorial board of phys.-math. lit.
- Zharkov, V. N. [1983], Inner structure of the Earth and planets. Moscow: Nauka, Chief editorial board of phys.-math. lit.
