Современные ДВС с кривошипно-шатунным механизмом принципиально не могут обеспечивать высокий термический КПД, который достигается при высоких степенях сжатия из-за возможной детонации, разрушающей подшипники коленчатого вала и срывающей масляную пленку с зеркала цилиндра.
Для достижения высоких степеней сжатия, и соответственно высокого КПД, требуется двигатель, обладающий следующими ключевыми свойствами:
- не имеет механической связи поршня с выходным валом, по крайней мере, в области высоких давлений цикла,
- отсутствует боковая нагрузка поршня на стенку цилиндра, и поэтому может работать без жидкой смазки в горячей зоне.
Таким двигателем является двухцилиндровый двухтактный двигатель, предложенный автором в [1].
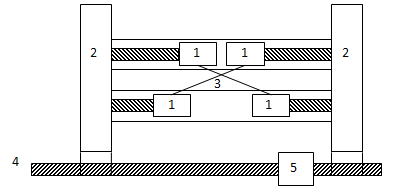
Уплотнительные кольца поршней предполагается изготавливать из графитового композита, что позволит отказаться от жидкой смазки. Отсутствие боковой нагрузки достигается благодаря соосности линии движения поршня и оси ротора. Связь поршня с ротором только магнитная, а в области высоких давлений (мертвых точек) она отсутствует. Схема двигателя представлена на рис.1.
Рис.1 Схема двухцилиндрового двигателя с противоположно движущимися поршнями и магнитной связью. 1 – поршни, 2 – роторы магнитного преобразователя, вращающиеся в противоположные стороны, 3 – жесткие «диагональные» связи поршней, 4 – выходной вал, 5 – редуктор-синхронизатор
Преобразователь возвратно-поступательного движения во вращательное является бесконтактным, основанным на магнитной связи магнитов штока поршня и вращающегося ротора [2].
Наличие нежесткой магнитной связи предполагает нетривиальную кинематику поршня и ротора, рассмотрение которой является целью данной работы.
Исходя из модели кинематики поршня, необходимо оценить диапазон рабочих частот, оптимальную частоту вращения ротора, мощность двигателя, параметры продувки.
Анимацию работы основных узлов двигателя можно посмотреть в [3].
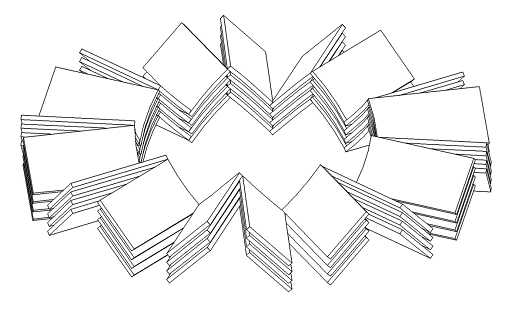
Расчетные значения будут представлены для двухцилиндрового двигателя конструкции, аналогичной [1], но с магнитом ротора в виде плоских пластин, расположенных под углом 90 градусов (см. рис.2)
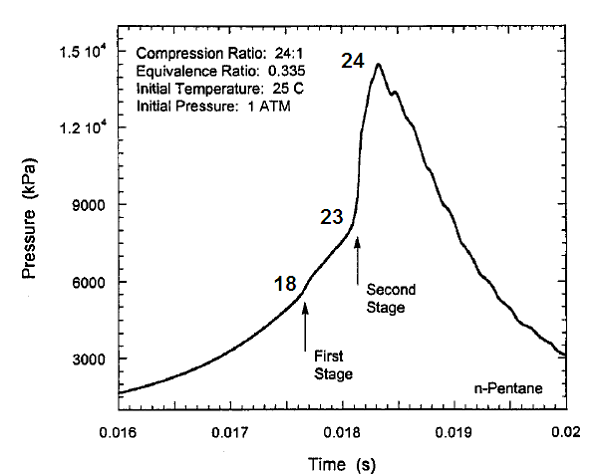
Экспериментальные данные по горению в режиме HCCI взятые из работы [4], показывают, что для достижения точки самовоспламенения, степень сжатия при использовании низкооктанового бензина должна составлять 23-24 единицы (рис. 3, данные для n-пентана, бедная смесь 0.335 от стехиометрической).
В предложенном двигателе степень сжатия переменная, зависит от условий каждого цикла сжатия и последующего сгорания.
Одним из модельных предположений будем считать адиабатичность процессов сжатия топливовоздушной смеси и расширения продуктов сгорания.
Значения хmin – минимальная координата поршня и xmax – максимальная координата, вообще говоря, различны для каждого цикла и зависят как от вида топлива, частоты движения поршней, так и от условий каждого акта воспламенения и сгорания. При этом эти значения должны соответствовать минимальным необходимым для самовоспламенения степеням сжатия. Очевидно, что хmin > 0, xmax - хmin ≤ L, где L – максимальная длина хода поршня.
В момент наибольшего сжатия смеси противодействующая сила со стороны магнитов ротора на магниты штока не действует. Поэтому большие усилия, возникающие в двигателе, в т.ч. при детонации смеси, в обычных ДВС передаются на шейку коленчатого вала и корпус двигателя, а в предложенном двигателе эти усилия лишь разгоняют противолежащие поршни, движущиеся фактически свободно. Существенную нагрузку растяжения при этом испытывает лишь стенка цилиндра и диагональные связи (штанги) поршней. Таким образом, прочность корпуса двигателя должна соответствовать не силам начальной стадии сгорания или детонации, а на порядок меньшим усилиям, передаваемым на выходной вал. Поэтому двигатель может выдерживать большие давления цикла без существенного утяжеления конструкции.
При адиабатическом расширении газа давление, а вместе с ней сила, падают очень быстро, поэтому пройдя небольшое расстояние, поршень испытывает уже вполне умеренные силы давления.
Для опытного образца в номинальном режиме работы сила уменьшается за время движения поршня от точки максимального давления до точки захвата магнитной силой в 5 раз.
Магнитные силы в двигателе
Изготовление магнитов ротора волнообразной формы [1] достаточно сложно с технологической точки зрения. Намного проще изготовить сборный магнит ротора из пластин, с торцевыми полюсами, установленными под углом (см. рис. 2).
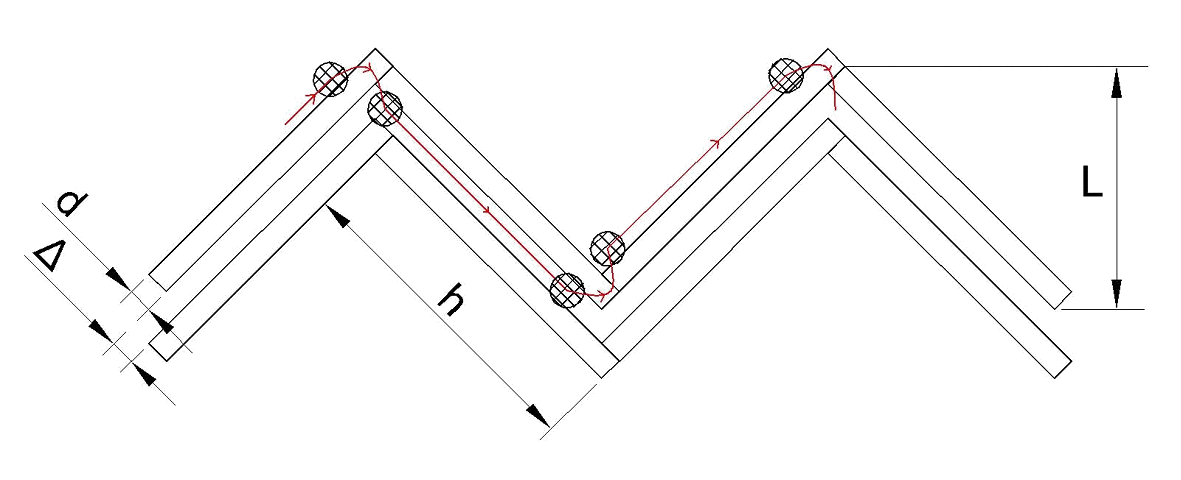
Развертка поверхности полюсов на плоскость выглядит следующим образом (рис.4):
Рис.4 Развертка внутренних полюсов магнитов ротора на плоскость. Кружками обозначен полюс магнита штока при его возвратно-поступательном движении. Слева схематично указан график магнитной силы в зависимости от положения полюса магнита штока. d – толщина магнита, ∆ – толщина разделителя магнитов, h – ширина магнита, L – расчетная длина хода поршня
Рассмотрим силы, действующие на магнит ротора в осевом направлении.
Сила давления продуктов сгорания топлива FД направлена вдоль оси движения поршня, а сила, направленная на вращение ротора FВ - перпендикулярно ей (см. рис.6)
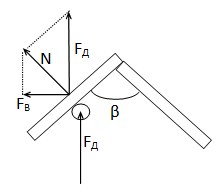
Касательной силы, действующей на магнит ротора нет, т.к. при перемещении полюса магнита штока вдоль полюса ротора сила не возникает. Механическая аналогия – тело на клине без трения, где на клин действует только нормальная сила со стороны тела.
Уравнения сил:
![]() ,
, ![]()
Максимальная сила давления, передаваемая магнитами, составит:
![]() .
.
Остальные магниты ротора и штока взаимодействуют аналогично, вклад каждого «слоя» магнитов в итоге суммируется.
Расчет в программе FEMM двумерной модели [2] показал для опытного образца вращающий момент системы магнитов М=2.07 Нм для каждого слоя магнитов. В каждом штоке и роторе опытного образца имеется 8 слоев. Таким образом, для всей системы имеется 16 слоев, и общий максимальный передаваемый вращающий момент составит Мдвиг = 33.12 Нм.
Для одного ротора вращающий момент опытного двигателя Mротор= 16.6 Нм, при плече силы R=5.8×10-2 м. Тогда максимальная магнитная вращающая сила одного ротора FВ= Mротор/R ≈ 286 Н.
Максимальная сила давления газов для угла в=90° составит FД=2FB=572 Н
При расчете режимов двигателя в дальнейшем считаем, что внешняя нагрузка является максимальной, т.е. соответствующей максимальной магнитной силе. В этих режимах будет развиваться максимальная мощность двигателя.
Кинематика прохода мертвой точки
Поскольку полюса крайнего магнита штока и крайнего магнита ротора имеют противоположную полярность, при проходе поршнем мертвых точек, магнитная сила меняет свой знак. При этом возникает эффект «свободного хода» поршня.
Считаем, что полюс поршня до некоторой точки «С» движется по средней линии разделителя магнитов. В этой точке «С» проекция скорости поршня на линию полюса ротора становится меньше проекции скорости ротора на эту же линию. При этом полюс поршня сходит со средней линии разделителя магнитов. Точку «С» назовем точкой сброса.
После точки сброса поршень тормозится силами давления сжимаемой топливо-воздушной смеси (ТВС), вплоть до полной остановки в точке хmin. При этом он проходит некое расстояние хС. Затем происходит самовоспламенение ТВС, поршень движется до средней линии разделителя магнитов, проходя некое расстояние xA (см. рис.7). Назовем точку «А» выхода поршня на эту линию точкой захвата. Отметим, что на средней линии разделителя магнитов на магнит штока (и жестко связанный с ним поршень) действует максимальная магнитная сила.
На рис.7 изображен фрагмент магнитной системы ротора, кружками обозначено положение полюса магнита штока в точках сброса (т.С), в мертвой точке (т.ВМТ) и в точке захвата (т.А)
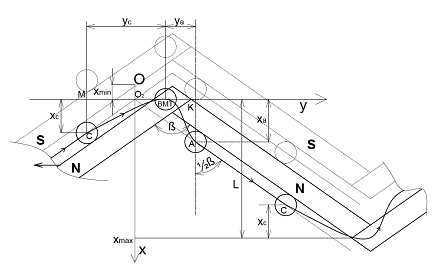
Рис. 7 Схема движения полюса штока относительно полюсов ротора вблизи мертвых точек. Система отсчета связана с внутренней поверхностью ротора, стрелкой указано направление движения ротора. Взаимодействующие полюса магнитов ротора и штока имеют различную полярность. Полярность магнитов ротора и штока чередуется в направлении движения штока. Точка О – начало координат, удобное для рассмотрения термодинамических процессов, точка О2 – начало координат для рассмотрения кинематики.
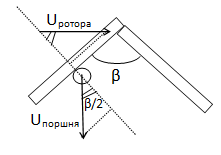
При синхронном движении полюс штока движется вдоль полюса ротора. Поэтому проекции скоростей полюсов штока и ротора на линию перпендикуляра к полюсу ротора должны иметь одинаковые значения (рис.8).
Приравнивая значения проекций, получим:
![]() , (1)
, (1)
где в – угол между полюсами ротора.
Таким образом, поршень «сбрасывается», когда скорость поршня становится меньше ![]() , и «захватывается» при достижении скорости
, и «захватывается» при достижении скорости ![]() . Обозначим скорости поршня, при которых происходит захват и сброс соответственно UЗ и UC.
. Обозначим скорости поршня, при которых происходит захват и сброс соответственно UЗ и UC.
Если угол между полюсами магнитов ротора в=900, скорости поршня и ротора при захвате одинаковы.
Качественная зависимость скоростей ротора и поршня от времени в приближении равноускоренного движения, для угла разворота полюсов в=90⁰ показана на рис. 9
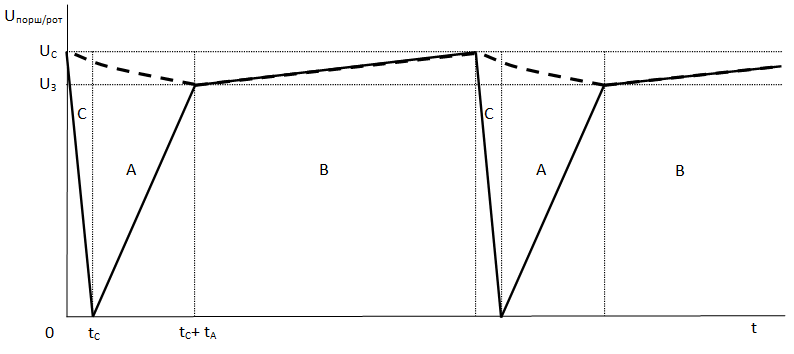
Рис. 9 График зависимости скоростей поршня и ротора от времени в приближении равноускоренного движения поршня. Прерывистой линией обозначена зависимость скорости ротора. Магниты ротора имеют прямоугольные полюса, расположенные под углом 90 градусов. Буквами обозначены фазы работы двигателя (описаны ниже).
Запишем основные кинематические соотношения для свободного хода поршня, считая движение равноускоренным с некоторым средним ускорением:
![]() ,
, ![]()
Приближенно будем считать, что ![]() , где асжат.мах - ускорение, действующее на поршень в конце такта сжатия, арасш.мах – ускорение, действующее на поршень в начале такта расширения. Тогда
, где асжат.мах - ускорение, действующее на поршень в конце такта сжатия, арасш.мах – ускорение, действующее на поршень в начале такта расширения. Тогда ![]() ,
, ![]() . Более точно время рассчитывается путем численного решения дифференциального уравнения типа
. Более точно время рассчитывается путем численного решения дифференциального уравнения типа ![]() с соответствующими краевыми условиями.
с соответствующими краевыми условиями.
Во время свободного хода поршня, скорость ротора меняется в соответствии с (1) от значения ![]() до
до ![]() . Приближенно считаем это движение равноускоренным, тогда средняя скорость ротора составит:
. Приближенно считаем это движение равноускоренным, тогда средняя скорость ротора составит:
![]()
Расстояние, пройденное точкой на внутренней поверхности ротора за время свободного пробега:
![]() (2)
(2)
Но, из рис.7 видно, что <О2СМ = <O2АК = в/2.
Тогда
![]()
Для расстояния, которое прошел ротор (а в системе отсчета ротора – расстояние пройденное полюсом магнита штока):
![]()
Сокращая ![]() , получаем условие для корректного прохождения мертвой точки:
, получаем условие для корректного прохождения мертвой точки:
![]() .
.
Как видим, от угла между пластинами магнита ротора соотношение не зависит. Введем обозначение:
![]()
Тогда окончательно получим условие:
![]() (3)
(3)
Значение величины д для каждого режима двигателя определяется с помощью численного исследования. С точки зрения физики процесса, д показывает, во сколько раз ротор движется быстрее, чем это нужно для того, чтобы поршень «успел» попасть на среднюю линию разделителя полюсов магнитов ротора. Для максимально эффективной работы эта величина должна быть равна 1.
Огибающая линия полюсов ротора может быть и не в виде ломаных прямых, а более сложной. Например, линия полюсов может быть волнистой линией или состоять из ломаных прямых с «плато» в области мертвых точек. Тогда расчет параметра д должен будет рассчитываться исходя из того, чтобы после прохождения поршнем расстояния ![]() он попадал на среднюю линию разделителя полюсов магнитов ротора.
он попадал на среднюю линию разделителя полюсов магнитов ротора.
Силовой расчет сечения поршня
В режиме передачи мощности тормозящий магнитный момент должен быть меньше или равен максимальному магнитному моменту. Для этого, после прохождения поршнем пути «свободного пробега», давление должно упасть до величины pраб = FД/S.
Для простоты, будем рассматривать термодинамические процессы только в одной половине цилиндра. В силу симметрии, величины работы, давления и силы одинаковы. Для получения итоговых значений мощности, полученные значения необходимо будет удвоить.
Считаем падение давления адиабатическим с показателем г=7/5:
pмаx (Vмаx)г = pраб (Vраб)г
Тогда, сокращая площадь поршня, получим:
pмаx = pраб ((xА+ xмin)/xмin)г,
где xА – часть длины свободного пробега поршня, его разбег, xmin – координата внутренней мертвой точки. Начало координат находится в центре цилиндра двигателя.
После окончания свободного пробега сила давления газов должна быть равна силе магнитной связи, в данном случае максимальной силе давления газов:
pраб S = FД, тогда
.gif) (4)
(4)
Механизм передачи мощности.
С точки зрения передачи мощности поршня к ротору, движение поршня состоит из трех фаз, повторяющихся каждый цикл.
Фаза А Первоначальный разгон поршня силами расширения сгоревшего (сдетонировавшего) топлива (1-2 на рис.10). Поршень движется без взаимодействия с ротором. Ротор немного снижает скорость под внешней нагрузкой. Точка захвата определяется силой магнитов, начальным давлением газов и текущей частотой ротора.
Фаза В Идет передача мощности за счет торможения ротором поршня. Движение поршня до некоторой конечной скорости «сброса» Uc, при которой ротор начинает обгонять поршень и передача мощности прекращается (2-3 на рис.10).
Фаза С Торможение поршня силами сжимаемой ТВС, вплоть до его остановки (3-4 на рис.10). Ротор немного снижает скорость под внешней нагрузкой.
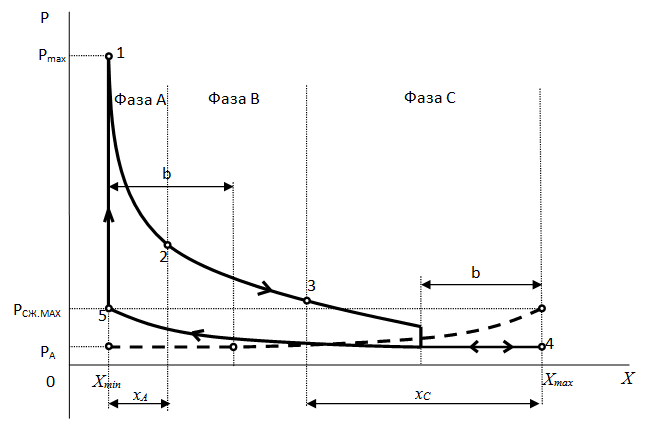
Считаем расширение газов адиабатическим с показателем г, то есть![]() , где pMAX – максимальное давление цикла при достижении внутренней мертвой точки, VMIN – объем Ѕ цилиндра при достижении внутренней мертвой точки. Тогда, учитывая, что сечение цилиндра не меняется, зависимость давления расширения от координаты будет иметь вид:
, где pMAX – максимальное давление цикла при достижении внутренней мертвой точки, VMIN – объем Ѕ цилиндра при достижении внутренней мертвой точки. Тогда, учитывая, что сечение цилиндра не меняется, зависимость давления расширения от координаты будет иметь вид:
![]() (5)
(5)
Аналогично, адиабата сжатия имеет вид ![]() , где pA – атмосферное давление, VСЖАТИЯ – объем Ѕ цилиндра при начале сжатия в соседнем цилиндре. Тогда зависимость давления сжатия от координаты будет иметь вид
, где pA – атмосферное давление, VСЖАТИЯ – объем Ѕ цилиндра при начале сжатия в соседнем цилиндре. Тогда зависимость давления сжатия от координаты будет иметь вид
![]() ,
,
где z – координата поршня в соседнем цилиндре.
Так как сжатие осуществляется в соседнем цилиндре, но из-за жестких «диагональных» связей – штанг, энергетически происходит за счет расширения в текущем цилиндре. Для учета в текущей координате x необходимо преобразование координат:
![]()
Тогда зависимость давления, действующего со стороны соседнего цилиндра, будет:
![]() (6)
(6)
Полная работа расширения, для Ѕ цилиндра, учитывая (5):
![]() (7)
(7)
Полная работа сжатия, для Ѕ цилиндра, учитывая (6):
.gif) (8)
(8)
Для расчета скоростей захвата и сброса необходимо также рассчитать работы фазы А и фазы С соответственно, для Ѕ цилиндра. Исходя из численных расчетов, xA < b, xC >b. Поэтому, учитывая работу сжатия в соседнем цилиндре:
![]() ,
,
.gif)
В этих фазах вся работа газов переходит в кинетическую энергию поршня и наоборот:
![]() ,
, ![]()
Скорости захвата и сброса, соответственно, составят: ![]() ,
, ![]() .
.
Максимальная работа, которая может быть совершена «половиной» цилиндра за рабочий такт двигателя:
Авнеш мах = FД(L – xA – xC) (9)
Отметим, что небольшие силы действуют также в фазах С и А, однако в рамках данной модели мы их не рассматриваем.
Передача мощности происходит в результате непосредственной работы газов в фазе B, а также за счет изменения скорости поршня. Это изменение скорости определяет неравномерность хода ротора. Коэффициент неравномерности:
.gif)
Расчеты для опытного образца показывают, что коэффициент неравномерности вращения в области рабочих частот близок к единице.
Энергетический расчет сечения поршня
Из уравнения энергетического баланса, в случае отбора максимальной мощности:
А+ + А- = Авнеш мах
Используя (7) и (8), а также (9), получим:
![]()
Раскрывая скобки, получим площадь сечения поршня:
![]() (10)
(10)
Необходимо отметить, что в формуле не учитываются потери двигателя на трение, потери давления в уплотнениях поршневых колец, потери на образование вихревых токов в магнитах и металлических частях двигателя. Однако эти потери должны быть невелики, в пределах 1-2 % мощности двигателя.
Расчет зависимости интервалов разгона и торможения
Для двигателя необходимо одновременное выполнение условий (4) и (10). Из решения получим, обозначив ![]() :
:
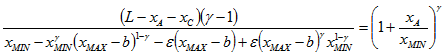
Обозначим ![]() .
.
Тогда условие соблюдения энергетического баланса и силы примет вид:
.gif) (11)
(11)
Расчет мощности на номинальной рабочей частоте
Мощность, развиваемая Ѕ цилиндра двигателя при условии полного использования магнитной силы:
![]()
Поскольку за один оборот ротора поршень совершает 2k ходов (для опытного образца 2k=9), а работают 2 половины цилиндра, мощность двигателя составит:
![]() (12)
(12)
Таблица 1 Вводные значения численного исследования
| Расстояние от середины цилиндра до внутренней мертвой точки | Xmin, мм | 0,6 |
| Расстояние от середины цилиндра до внешней мертвой точки | Xmax, мм | 19,1 |
| Ход поршня | L, мм | 18,5 |
| Атмосферное давление | Pa, Па | 101325 |
| Максимальное давление цикла | Pmax, Па | 15000000 |
| Длина выпускных окон по зеркалу цилиндра | b, мм | 3,0 |
| Показатель адиабаты воздуха и ТВС | г | 1,4 |
| Внутренний радиус ротора | r, мм | 58,0 |
| Масса поршня | m, кг | 0,7 |
| Максимальная сила, передаваемая магнитной системой | Fд, Н | 572 |
| Угол разворота магнитных полюсов ротора | в | 90 |
| Степень сжатия | ж | 26,8 |
| Термический КПД цикла | з | 73,2 |
Таблица 2. Результаты численного исследования
|
Ха,мм
|
Хс,мм
|
Диаметр цилиндра D, мм
|
UЗ, м/с
|
UС , м/с
|
Частота n, мин-1
|
Uз/Uc
|
Мощ-ность N, Вт
|
N, л.с.
|
Рабочий объем, см3
|
Удель-ная мощ-ность, кВт/л
|
д
|
|
0,1
|
16,1176
|
7,7627
|
0,4265
|
1,2298
|
856,7
|
0,3
|
107
|
0,1
|
3,5016
|
29
|
0,339
|
|
0,2
|
15,5485
|
8,5233
|
0,6314
|
1,3469
|
1023,2
|
0,5
|
154
|
0,2
|
4,2213
|
35
|
0,404
|
|
0,3
|
14,9552
|
9,2558
|
0,8047
|
1,4586
|
1170,6
|
0,6
|
208
|
0,3
|
4,9781
|
40
|
0,457
|
|
0,4
|
14,3395
|
9,9642
|
0,9624
|
1,5655
|
1307,5
|
0,6
|
269
|
0,4
|
5,7693
|
45
|
0,504
|
|
0,5
|
13,7027
|
10,6517
|
1,1105
|
1,6678
|
1437,0
|
0,7
|
337
|
0,5
|
6,5929
|
49
|
0,550
|
|
0,6
|
13,0460
|
11,3206
|
1,2516
|
1,7660
|
1560,8
|
0,7
|
414
|
0,6
|
7,4470
|
53
|
0,594
|
|
0,7
|
12,3704
|
11,9730
|
1,3875
|
1,8600
|
1679,7
|
0,7
|
498
|
0,7
|
8,3300
|
57
|
0,639
|
|
0,8
|
11,6768
|
12,6105
|
1,5191
|
1,9501
|
1794,4
|
0,8
|
590
|
0,8
|
9,2407
|
61
|
0,686
|
|
0,9
|
10,9660
|
13,2345
|
1,6472
|
2,0360
|
1905,1
|
0,8
|
690
|
0,9
|
10,1778
|
65
|
0,736
|
|
1,0
|
10,2387
|
13,8461
|
1,7722
|
2,1177
|
2012,0
|
0,8
|
798
|
1,1
|
11,1402
|
69
|
0,789
|
|
1,1
|
9,4955
|
14,4463
|
1,8946
|
2,1948
|
2115,2
|
0,9
|
913
|
1,2
|
12,1270
|
72
|
0,847
|
|
1,2
|
8,7369
|
15,0360
|
2,0146
|
2,2670
|
2214,6
|
0,9
|
1036
|
1,4
|
13,1373
|
76
|
0,912
|
|
1,3
|
7,9636
|
15,6160
|
2,1324
|
2,3337
|
2310,0
|
0,9
|
1166
|
1,6
|
14,5703
|
79
|
0,984
|
|
1,4
|
7,1759
|
16,1869
|
2,2484
|
2,3937
|
2401,1
|
0,9
|
1302
|
1,8
|
15,7253
|
82
|
1,066
|
|
1,5
|
6,3744
|
16,7493
|
2,3626
|
2,4459
|
2487,1
|
1,0
|
1444
|
2,0
|
16,3017
|
85
|
1,160
|
|
1,6
|
5,5593
|
17,3037
|
2,4751
|
2,4879
|
2567,1
|
1,0
|
1590
|
2,2
|
17,3987
|
88
|
1,270
|
|
1,7
|
4,7311
|
17,8506
|
2,5861
|
2,5165
|
2639,3
|
1,0
|
1740
|
2,4
|
18,5159
|
91
|
1,400
|
|
1,8
|
3,8901
|
18,3904
|
2,6957
|
2,5257
|
2700,7
|
1,1
|
1890
|
2,6
|
19,6526
|
93
|
1,556
|
|
1,9
|
3,0367
|
18,9235
|
2,8040
|
2,5048
|
2745,9
|
1,1
|
2035
|
2,8
|
20,8085
|
94
|
1,742
|
|
2,0
|
2,1712
|
19,4502
|
2,9111
|
2,4304
|
2762,9
|
1,2
|
2163
|
2,9
|
21,9830
|
95
|
1,963
|
|
2,1
|
1,2937
|
19,9709
|
3,0169
|
2,2392
|
2718,7
|
1,3
|
2244
|
3,1
|
23,1758
|
93
|
2,191
|
|
2,2
|
0,4047
|
20,4858
|
3,1217
|
1,6332
|
2459,4
|
1,9
|
2136
|
2,9
|
24,3863
|
84
|
2,147
|
Параметры Таблице 1 выбирались исходя из расчетов в программе Дизель-РК [5], экспериментальных данных [4], а также параметров магнитной системы, рассчитанных в [1].
Для получения расчетных данных Таблицы 2 использовался диапазон значений xA от 0.5 мм до 2.2 мм с шагом 0.1 мм. Верхний предел обусловлен неотрицательностью xС, в соответствии с соотношением (11). Расчет производился по формулам (5)-(12).
Выделены строки, значения в которых подходят для номинального режима работы с д=1. В этом режиме приемлемая неравномерность ч=0.9, при необходимости ее можно скомпенсировать эксцентриковыми шкивами.
Для опытного образца была выбрана номинальная частота вращения ротора 2400 об/мин, при этом мощность составит 1300 Вт. Диаметр поршней 16,2 мм, а рабочий объем всего двигателя около 16 куб. см, при удельной мощности 82 кВт/л. Расчетный термический КПД составил 73,2%.
Регулирование мощности
Поскольку количество воздуха в каждом такте практически неизменно, а частота вращения, как мы видели, не должна меняться, регулирование мощности производится изменением степени обогащения топлива. Применительно к рассматриваемой модели, меняться будет максимальное давление цикла. Считаем при этом, что степень сжатия не изменяется.
Таблица 3 Зависимость расчетных параметров от максимального давления цикла
| Pmax, Па | Ха | Хс | Частота n, мин-1 | Uз/Uc | Мощность N, Вт | д |
|
10000000
|
0,8971
|
10,9868
|
2329,4
|
0,8
|
842
|
0,864466
|
| 11000000 |
1,0026
|
10,2198
|
2352,6
|
0,8
|
935
|
0,894955
|
| 12000000 |
1,1053
|
9,4554
|
2370,9
|
0,9
|
1028
|
0,929544
|
| 13000000 |
1,2057
|
8,6935
|
2384,8
|
0,9
|
1121
|
0,96905
|
| 14000000 |
1,3038
|
7,9337
|
2394,8
|
0,9
|
1212
|
1,014347
|
| 15000000 |
1,4000
|
7,1759
|
2401,1
|
0,9
|
1302
|
1,066451
|
| 16000000 |
1,4944
|
6,4200
|
2403,6
|
1,0
|
1390
|
1,126582
|
| 17000000 |
1,5870
|
5,6657
|
2402,0
|
1,0
|
1476
|
1,196226
|
| 18000000 |
1,6782
|
4,9129
|
2395,7
|
1,0
|
1559
|
1,277162
|
| 19000000 |
1,7679
|
4,1616
|
2383,4
|
1,1
|
1637
|
1,371403
|
| 20000000 |
1,8562
|
3,4116
|
2363,1
|
1,1
|
1708
|
1,480821
|
| 21000000 |
1,9434
|
2,6629
|
2330,8
|
1,1
|
1769
|
1,605703
|
| 22000000 |
2,0293
|
1,9154
|
2278,1
|
1,2
|
1811
|
1,739342
|
| 23000000 |
2,1141
|
1,1690
|
2182,7
|
1,4
|
1815
|
1,844677
|
| 24000000 |
2,1979
|
0,4236
|
1953,8
|
1,9
|
1695
|
1,706957
|
Определившись с номинальным режимом работы и определив диаметр поршня, можем из (4) получить значение xA:
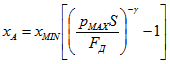 (13)
(13)
Формулы (11) и (13) позволяют рассчитать мощность в зависимости от максимального давления. Результаты расчетов для опытного образца двигателя представлены в таблице 3.
Из таблицы 3 видим, что возможно регулирование мощности путем изменения состава ТВС, в пределах 900 – 1500 Вт, при неизменной степени сжатия. Меньшие значения мощности соответствуют степени сжатия, при которой не гарантируется самовоспламенение смеси.
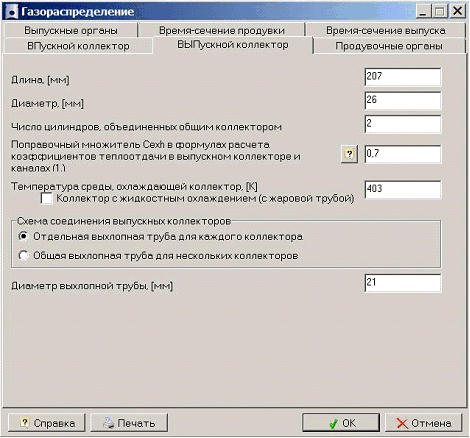
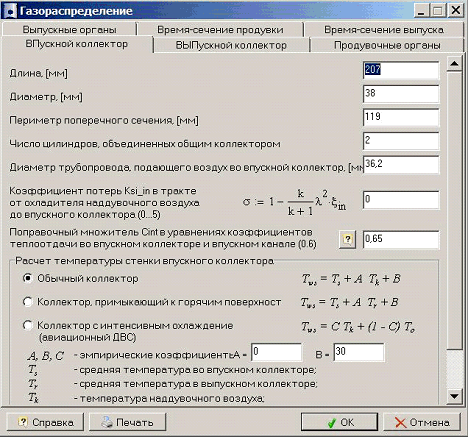
Расчет газообмена
Двигатель имеет прямоточно-щелевую продувку, встречные поршни движутся строго в противофазе. При этом выпускные окна открываются раньше впускных и позже закрываются, что обеспечивается большей длиной выпускных окон по зеркалу цилиндра. Для расчета формы и оптимального сечения окон использовалась программа Дизель-РК [5], а также работа [6].
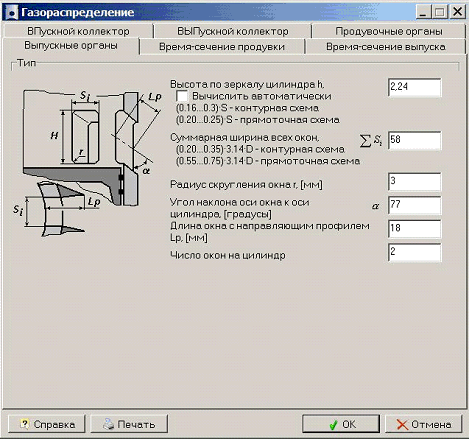
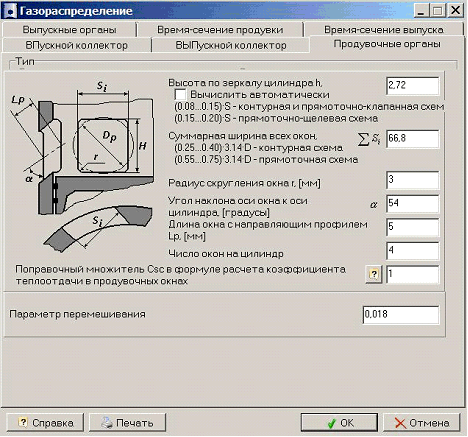
Двигатель, предложенный в [1], является с точки зрения программы Дизель-РК нестандартным, но мы можем считать, что он аналогичен встречно-поршневым дизелям с теми же размерами камеры сгорания.
Пути совершенствования двигателя
В предложенном двигателе противоположные поршни двигаются в противофазе, в отличие от классических двигателей со встречно-движущимися поршнями, где фазы продувочных и выпускных поршней сдвинуты для возможности использования наддува.
Поэтому более раннее закрытие выпускных окон необходимо обеспечивать, при необходимости, например, наддува, дополнительным устройством – гильзовым клапаном или заслонкой в выпускном коллекторе, с соответствующим управлением. Управление гильзами или заслонками проще всего осуществить от возвратно-поступательного движения соединительных штанг. Тогда продувочный насос будет работать также как нагнетатель. Использование турбонаддува представляется нецелесообразным из-за высокой степени сжатия, и, следовательно, расширения. При этом температура и скорость выхлопа не будут большими.
Одним из путей увеличения литровой мощности двигателя может быть увеличение частоты, что достигается увеличением длины хода L и силы магнитов FД. Кроме того, форсирование по частоте может быть применено путем изменения геометрии магнитов ротора, в частности, «плато» (см. рис.13)
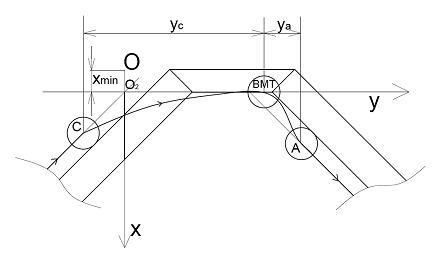
Благодаря увеличенному пути ротора, при том же пути поршня, можно соблюсти условие (3) для более высоких мощностей и частот вращения.
В силу отсутствия масляной пленки на зеркале цилиндра и химической пассивности графитовых колец, перспективным представляется непосредственный впрыск топлива в цилиндр вместе с водой или растворами активных веществ. В качестве активного вещества можно использовать карбамид, свойства его как поглотителя оксидов азота и серы хорошо изучены [7,8].
Выводы
Двигатель по своим характеристикам подходит для нагрузок с постоянной частотой вращения:
- гибридные транспортные средства,
- генераторы электроэнергии,
- крупнотоннажные суда и локомотивы,
- привод компрессоров и другого оборудования.
Исходя из расчетов, двигатель обладает высоким для тепловых машин термическим КПД и высокой удельной мощностью. Благодаря своим конструктивным особенностям, нейтрализация оксидов азота и серы в двигателе может производиться непосредственно в цилиндре.
Библиографический список
- Сухаревский В.В. Преобразователь возвратно-поступательного движения во вращательное и двухцилиндровый двигатель на его основе // Современные научные исследования и инновации. 2014. № 10 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2014/10/39944 (дата обращения: 22.10.2015)
- Youtube, http://www.youtube.com/watch?v=CGNBFX1FHgA
- Заявка РСТ/RU 2014/000486 от 30.06.2014
- Van Blarigan P., Goldsborough S. Homogeneous charge compression ignition free piston linear alternator. Sandia report SAND99-8206, November 1998
- Программа Дизель-РК http://www.diesel-rk.bmstu.ru/Rus/
- Орлин. Расчет сечений органов распределения двухтактных быстроходных двигателей. – М:Труды ЦИАМ, Выпуск 28, 1938, с. 62
- Фролов С.Г., Росляков А.Д. Уменьшение вредных выбросов транспортных дизелей путем нейтрализации оксидов азота // Вестник Самарского государственного аэрокосмического университета, 2009, №3(19), с. 138-142
- Демидов А.А., Надарейшвили Г.Г. Контроль концентрации аммиака в системах селективного восстановления оксидов азота дизелей // Механика машин, механизмов и материалов. 2015. № 3 (32), с. 43-46