Введение

Основным уравнением, из которого вытекала гипотеза Луи де Бройля о волновых свойствах материи, была формула, записанная им на основании гипотезы Планка о наименьшем кванте энергии и уравнения Эйнштейна, связывающего массу и энергию, . Из нее следовало, что каждой порции энергии, обладающей массой  , соответствует периодический процесс, частота которого равна .

Применение гипотезы де Бройля к элементарным частицам, в частности к электрону, будет означать, что электрон содержит внутренний волновой процесс. Но в свое время этот волновой процесс не был обнаружен и волны де Бройля стали ассоциироваться только с механическим движением частиц.

Современная физика интерпретирует волны де Бройля как волны вероятности, не имеющие материального воплощения.

В последнее время, появились экспериментальные факты, подтверждающие первоначальную гипотезу де Бройля о существовании волн материи [3], [4].

Эти экспериментальные результаты стимулировали появление многочисленных попыток теоретического объяснения [7], [8].

В настоящей работе, путем решения релятивистского уравнения М2 [2] будет показано, что элементарные частицы, в частности электрон, вполне могут содержать волновой процесс с весьма специфическими свойствами. Волновая модель неподвижного электрона представляется в виде сферического волнового процесса.

Данную статью можно скачать в формате PDF по ссылке - https://portalnp.snauka.ru/wp-content/uploads/2016/01/VolnovayaFunkciaElektrona1.pdf

Нестационарное уравнение М2

Преобразуем полученное в работе [2] стационарное релятивистское уравнение М2 (1.1) в нестационарную форму.

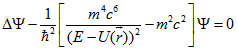 (1.1)

Для этого удаляем из уравнения потенциальную энергию  и подставляем зависящее от времени и волновой функции значение квадрата энергии в уравнение.

В результате получим: 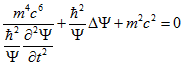 (1.2)

Теперь необходимо найти дисперсионное соотношение для полученного уравнения (1.2).

Для этого подставим сферическую волну  (1.3) в уравнение.

Определим второе производное по времени:  (1.4)

Оператор Лапласа в сферической системе координат имеет следующий вид:

 (1.5)

Определим результат действия оператора Лапласа на сферическую волну:

 (1.6) Подставим сферическую волну (1.3) и полученные значения (1.4) и (1.6) в исходное нестационарное уравнение (1.2).

В результате получим дисперсионное соотношение в виде:  (1.7)

 

Волна без дисперсии и волновой пакет без расплывания

 

Для полученного дисперсионного соотношения, определим фазовую и групповую скорости распространения волн.

Как известно фазовая скорость определяется через круговую частоту  и волновое число по формуле:  (2.1)

Из уравнения (1.7) определим круговую частоту .  (2.2)

Подставим полученное значение (2.2) в формулу (2.1) 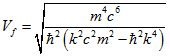 (2.3)

Групповая скорость определяется по формуле:  (2.4). Определим производную пользуясь формулой (2.2).  (2.5).

Построим графики зависимости фазовой и групповой скоростей от волнового числа . Далее будем пользоваться атомной системой единиц Хартри.

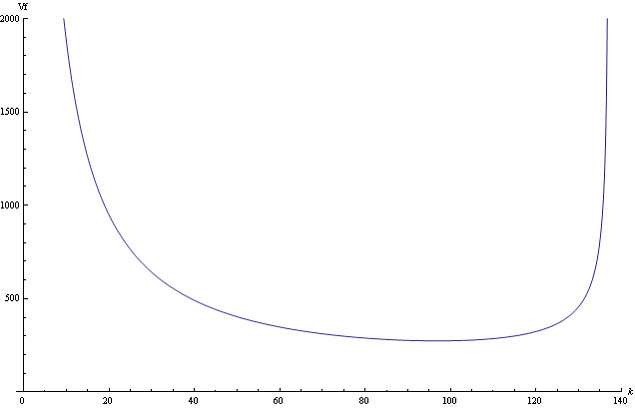
Рис.1 График зависимости фазовой скорости от волнового числа .

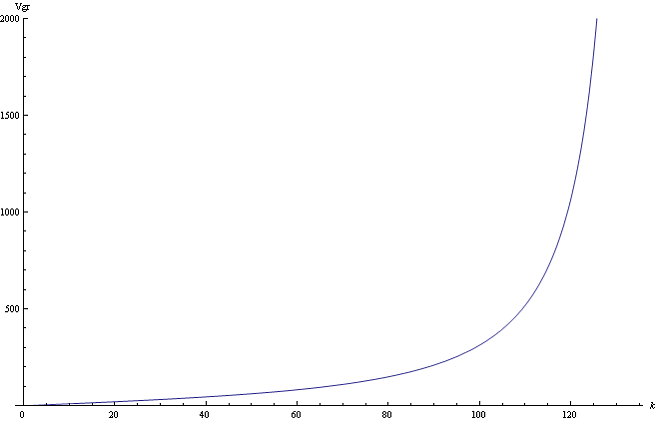
Рис.2 График зависимости групповой скорости  от волнового числа .

Теперь совместим оба графика на одном рисунке.

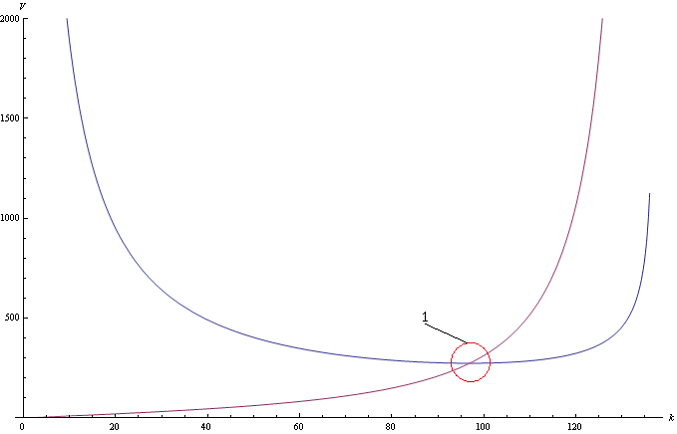
Рис.3 Совместный график фазовой и групповой скоростей.

Как можно заметить, при определенном значении волнового числа, фазовая скорость равняется групповой скорости.

Приравнивая соответствующие формулы  и решая полученное уравнение, определяем значение волнового числа устойчивого состояния:  (2.6). При этом значение скорости будет . И соответствующее значение круговой частоты получим:  (2.7). Таким образом, мы получили сферическую волну без дисперсии. Так как, при условии равенства фазовой и групповой скоростей, дисперсия исчезает.

Полученное значение скорости в два раза выше скорости света. Но это не скорость движения электрона. Так как мы рассматриваем электрон в неподвижном состоянии. Это скорость распространения в пространстве сферической волны де Бройля (для первоначальной версии гипотезы), то есть волны материи. И поскольку полученная волна материи пока что имеет неизвестную природу, то пока не будем ограничивать ее характеристики и в частности скорость распространения.

Прежде чем продолжить, обратим внимание на следующее обстоятельство. Определим энергию покоя электрона в соответствии с формулой . Тогда получим . Как можно заметить, полученное значение энергии, в  раза больше ожидаемого значения, энергии покоя электрона .

Для устранения полученного несоответствия, введем понятие затравочной массы электрона. Которая вступая во внутренние волновые процессы, образует энергию покоя . Из этих соображений получим значение затравочной массы . И в дальнейших расчетах вместо массы электрона будем применять затравочную массу.

Тогда окончательно получим для устойчивого состояния значение волнового числа  (2.8) и значение круговой частоты  (2.9).

Интегрируя сферические волны в небольшой окрестности  устойчивого состояния (область 1 Рис.3.). Можно получить сферический волновой пакет без расплывания (2.10).

 (2.10)

Теперь, после получения параметров устойчивого состояния электрона, имеет смысл перейти к стационарному уравнению и окончательно получить волновую функцию голого неподвижного электрона.

Для этого, подставим полученное значение затравочной массы  и значение энергии покоя  в исходное стационарное уравнение (1.1) без потенциальной энергии. Тогда получим:  (2.11)

Полученное уравнение, в теории дифференциальных уравнений, известно как уравнение Гельмгольца.

Решение уравнения Гельмгольца

Для решения уравнения (2.11) применим стандартную методику разделения переменных в сферической системе координат.

Представим волновую функцию в виде произведения радиальной и угловой частей (3.1)

Оператор Лапласа в сферических координатах выглядит следующим образом:  (3.2) Подставим произведение (3.1) в исходное уравнение (2.11).

 Умножим полученное уравнение на дробь .

 (3.3) Как можно заметить левая часть уравнения (3.3) зависит только от переменной  , а правая от переменных  и . Следовательно, обе части равны некоторому постоянному числу . Что позволяет отделить радиальную часть уравнения от угловой части.

 (3.4)  (3.5) Далее представим функцию  в виде произведения  (3.6). Угловая часть оператора Лапласа имеет следующий вид:  (3.7). Подставим произведение (3.6) в угловое уравнение (3.5) получим:  (3.8).

Умножив уравнение (3.8) на дробь  получим:  (3.9) Левая часть уравнения (3.9) зависит только от переменной  а правая часть только от переменной . Следовательно, обе части равны некоторому постоянному числу, которую обозначим . В итоге получим два уравнения: (3.10) и  (3.11)

Решение уравнения (3.11) хорошо известно  (3.12). Так как при тождественных значениях угла  ( и ) функция должна иметь одно и то же значение, то  и . Используя формулу Эйлера для комплексных чисел: , получим  Таким образом,  может принимать только целочисленные значения. Константа находится из условия нормировки функции . Но поскольку стандартная нормировка и вероятностная интерпретация волновой функции теперь уже не действуют, то пока этот вопрос обсуждать не будем.

Для решения уравнения (3.10), воспользуемся математическим интернет ресурсом WolframAlpha http://www.wolframalpha.com/

Решение дает:  (3.13)

То есть, решением является, сумма присоединенных функций Лежандра первого и второго рода.

Сделаем обозначение  (3.14). Переменная  у нас будет ассоциироваться с квантовым числом спина. Определим область возможных значений квантового числа. Из формулы (3.14) следует, что  следовательно  (3.15). Переписав зависимость (3.14) относительно  получим  (3.16) как и следовало ожидать. Таким образом угловая часть волновой функции будет иметь вид:

 (3.17)

Поскольку у нас электрон находится в неподвижном состоянии, то обычные условия квантования орбитального момента не имеют места. Поэтому пока не можем говорить, что квантовое число  может принимать только целые или полуцелые значения. Область возможных значений  будет ограничиваться только соотношением (3.15) и условием неразрывности угловой части волновой функции (3.17). Конкретные значения квантовых чисел  и  и констант интегрирования  и  будут зависеть от внешних факторов. То есть от граничных условий конкретной задачи. В работах автора [5] приведен подход, согласно которому квантовые числа  и  могут принимать как целые так и полуцелые значения. Мы считаем этот подход разумным.

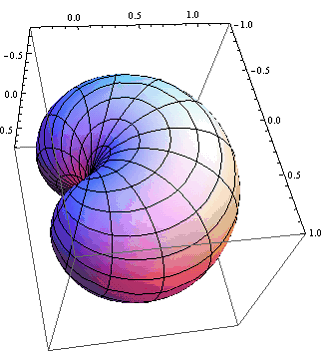
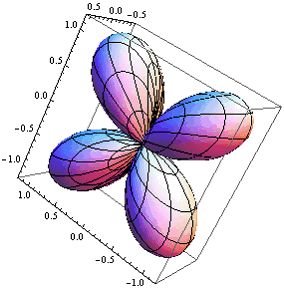
Приведем для наглядности несколько графических примеров угловой части волновой функции при различных значений квантовых чисел  и .

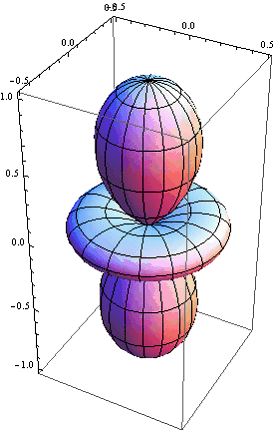
Перейдем к решению радиального уравнения (3.4). Для этого воспользуемся математическим интернет ресурсом WolframAlpha http://www.wolframalpha.com/

Перепишем уравнение (3.4) с учетом обозначения (3.16).

 (3.18)

Решение имеет вид:  (3.19)

То есть является комбинацией сферических функций Бесселя первого и второго рода. Как известно, сферическая функция Бесселя второго рода неограничена при . Поэтому принимаем . И окончательно радиальная часть волновой функции будет иметь вид:

 (3.20)

Приведем график радиальной волновой функции в атомных единицах Хартри, для первых нескольких значений квантового числа . Поскольку вопрос нормировки пока не обсуждаем, по приведенным причинам, то примем . В единицах Хартри масса электрона , постоянная Планка и скорость света .

Рис. 4. График радиальной части волновой функции при значениях 

 

Таким образом, полная волновая функция электрона будет представлять, произведение радиальной, угловой и зависящей от времени частей.

 (3.21)

Результаты и обсуждения

Как было показано, электрон имеет внутренний волновой процесс с частотой . Волновой процесс выходит в наружу и образует волны материи. При этом волновое число равно , следовательно длина волны равна , а скорость распространения в пространстве двукратно превышает скорость света. Следовательно, волны материи имеют не электромагнитную природу.

Как известно, электрон характеризуется экспериментально обнаруженным значением: длиной волны Комптона . Следовательно, полученная длина волны составляет двукратную величину Комптоновской длины волны . Отсюда можно сделать предположение, что Комптоновская длина волны связана с волновыми свойствами электрона.

В свое время Э. Шредингер не был согласен с чисто корпускулярным объяснением эффекта Комптона. И опубликовал свое волновое описание [9].

“Шредингер утверждал, что рентгеновское излучение может дифрагировать на стоячей “волне плотности заряда”, созданной падающим и отраженным электроном, так же как свет дифрагирует на стоячей волне ультразвука (Born and Wolf 1959).”

Далее обнаружено, что в колебательном процессе участвует не вся масса электрона. В результате, вводится понятие затравочной массы . То есть, масса электрона формируется, в результате вступления затравочной массы во внутренний волновой процесс. По аналогии можно предположить, что и затравочная масса тоже образуется в результате волнового процесса второй ступени. И следовательно, материя имеет многоступенчатую, вложенную друг в друга волновую структуру, как матрешка.

Установлено, что спин электрона не обязательно должен иметь значение . Область возможных значений квантовых чисел электрона еще предстоит изучать.

Полученные результаты открывают новые горизонты для теоретических и экспериментальных исследований. Позволяют по новому взглянуть на многие экспериментальные результаты, в которых фигурируют волновые свойства электрона.

Библиографический список

1. Луи де Бройль. Избранные научные труды. Т. 1. Становление квантовой физики: работы 1921 – 1934 годов. – М.: Логос, 2010. – 556 с.
2. Дангян А.Э. “Новое уравнение релятивистской квантовой механики”
3. Gouan`ere, M. et al., Experimental observation compatible with the particle internal clock, Annales de la Fondation Louis de Broglie 30, 109-114 (2005)
4. A search for the de Broglie particle internal clock by means of electron channeling P.Catillon, N.Cue, M.J.Gaillard, R.Genre, M.Gouanère, R.G.Kirsch, J-C.Poizat, J.Remillieux, L.Roussel and M.Spighel
5. Квантовая теория полей движения Д.В.Гламазда Уральский федеральный университет, Екатеринбург 18 октября 2011 г.  http://quantt.ru/
6. Холодова С.Е., Перегудин С.И. Специальные функции в задачах математической физики. – СПб: НИУ ИТМО, 2012. – 72 с.
7. On electron channeling and the de Broglie internal clock M. Bauer Instituto de F´ısica, niversidad Nacional Aut´onoma de M´exico and A.P. 20-364, 01000 M´exico, D.F., MEXICO
8. Hunting for Snarks in Quantum Mechanics David Hestenesa Physics Department, Arizona State University, Tempe, Arizona 85287.
9. Srhrodinger E. The Compton effect. Annalen der Physik. 1927. V. 28. P. 257 – 264.

---

Количество просмотров публикации: Please wait

Все статьи автора «Дангян Араик Эмильевич»