Введение

Задача определения прочности металлоконструкции и её остаточного ресурса является актуальной для объектов повышенной опасности, таких как, например, ядерная энергетическая установка. При этом требуется максимально точное определение механических характеристик металла, отражающих его состояние с точки зрения прочности.

В предшествующих работах [1-3] была рассмотрена задача определения стандартизованных механических характеристик (предел текучести и степенной показатель упрочнения)  по диаграмме индентирования, являющейся результатом проведения испытаний на вдавливание индентора в исследуемый образец металла. Было показано, что эта задача является плохо обусловленной [4-6]. Плохая обусловленность проявляется в высокой степени изменений значений механических характеристик при незначительных изменениях параметров диаграммы индентирования. Для некоторых видов сталей отклонение параметров диаграммы не более чем на 1% может приводить к 13% изменению значения предела текучести. В таких условиях требуется применение специальных мер для получения высокоточных оценок механических характеристик металла, удовлетворяющих практическим требованиям.

В статье [7] для решения плохо обусловленных задач, характеризующихся описанными выше особенностями, предложено использовать комитет нейронных сетей оригинальной архитектуры наряду с использованием регуляризации [8, 9]. Разработанный комитет позволяет оценить значения механических характеристик металла по соответствующей диаграмме индентирования. Естественным ограничением при этом является использование отдельного предварительно настроенного комитета для каждого конкретного типа металла, обладающего известным диапазоном изменения значений предела текучести и степенного показателя упрочнения. Для унификации разработанного метода и его расширения на различные группы сталей требуется использование дополнительного модуля. В качестве такого модуля в текущей работе предлагается использовать нейросетевой классификатор.

 1.      Постановка задачи. Исходные данные

Процесс определения значений механических характеристик в таком случае организован в последовательности, схематично представленной на рисунке 1. На начальном этапе при помощи классификатора определяется тип металла по известным характеристикам диаграммы индентирования. В качестве таких характеристик используются коэффициенты аппроксимации диаграммы кубической параболой. Затем из предварительно обученного набора комитетов нейронных сетей выбирается один, соответствующий определённому ранее типу металла. При помощи выбранного комитета на основании параметров диаграммы индентирования вычисляются значения предела текучести и степенного показателя упрочнения.

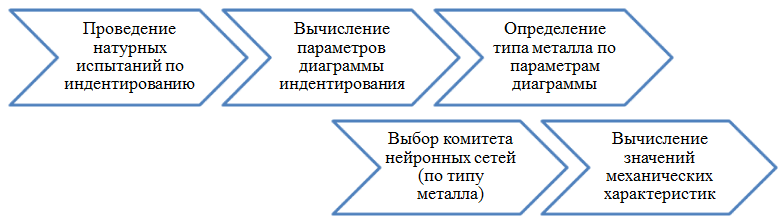
Рисунок 1 - Последовательность действий для определения значений механических характеристик при помощи нейросетевого подхода

В результате, для каждого типа металла требуется обучить отдельный нейросетевой комитет и построить классификатор. Всего в работе рассматривается четыре различных вида сталей, характеристики которых представлены в таблице 1.

Таблица 1 – Характеристики исследуемых образцов металлов

Каждая диаграмма для рассматриваемых типов металлов может быть аппроксимирована кубической параболой, проходящей через точку (0; 0) в пространстве координат «приложенная к индентору сила –  глубина вдавливания индентора». Таким образом, в качестве входных параметров всех нейронных сетей, входящих в состав комитета, используются значения трёх аппроксимационных коэффициентов диаграммы индентирования. Для снижения корреляции ошибок работы сетей, каждая из них обучается на отдельной подвыборке исходного набора данных. Обучающие наборы могут пересекаться для различных сетей, но не могут совпадать полностью.

 2.      Экспериментальные результаты

Исследование особенностей данных показало, что для каждого типа металла с целью уменьшения погрешности целесообразно осуществлять моделирование предела текучести и степенного показателя упрочнения на отдельных комитетах сетей. Следовательно, всего было обучено восемь комитетов: по два для каждого класса стали. Все они имели одинаковую архитектуру, квантильное решающее правило [10] и состояли из 10 многослойных персептронов. Рабочие сети комитетов, определяющих значение степенного показателя упрочнения, содержали два скрытых слоя по три нейрона в каждом; комитетов, предназначенных для определения степенного показателя упрочнения – два скрытых слоя по пять нейронов в каждом. Активационные характеристики скрытых слоёв сигмоидальные, выходного слоя – линейные. Результаты обучения комитетов представлены в таблице 2. Полученная погрешность определения предела текучести менее 10% соответствует практическим требованиям.

Таблица 2 – Погрешность определения значений механических характеристик комитетами нейронных сетей

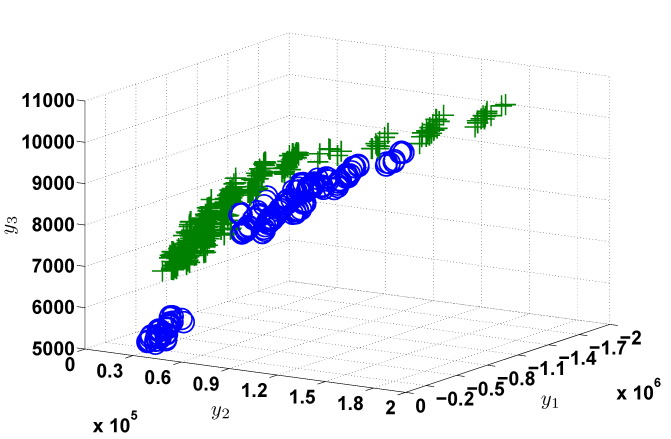
С целью определения метода построения классификатора для исследуемых типов сталей, рассмотрим пример распределения параметров экспериментальных диаграмм индентирования, соответствующих образцам сталей 20 и Х18Н10Т. Соответствующий график представлен на рисунке 2. По координатным осям отложены значения трёх аппроксимирующих коэффициентов, однозначно идентифицирующих каждую диаграмму. Образцы, соответствующие стали 20, отмечены на графике плюсами, стали Х18Н10Т – кругами. Видно, что два этих класса сталей не являются линейно разделимыми в рассматриваемом пространстве признаков. Такая задача классификации может быть решена с использованием нескольких элементарных персептронов с бинарными активационными характеристиками. Построение нейросетевого классификатора на основе элементарных персептронов осуществляется при помощи классического алгоритма, предложенного Мезардом и Надалом [11].

Рисунок 2 – Распределение параметров диаграмм индентирования для сталей 20 и Х18Н10Т

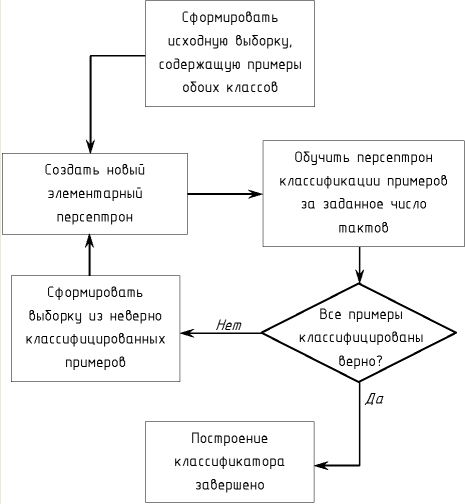
Схема алгоритма Мезарда-Надала представлена на рисунке 3. На первом этапе осуществляется формирование обучающей выборки, содержащей все примеры, принадлежащие обоим классам сталей. Затем создаётся первый персептрон (он состоит из одного нейрона), который в течение заданного количества тактов обучается классификации примеров в выборке. Поскольку исходные классы не являются линейно разделимыми, то процесс обучения такого персептрона является бесконечным и должен быть остановлен принудительно. После того, как обучение первого персептрона останавливается, требуется определить все примеры, которые были классифицированы им неверно. Они формируют выборку, на которой будет обучаться второй персептрон. Затем будут отобраны образцы, которые он классифицирует ошибочно и так далее до тех пор, пока все примеры не будут классифицированы верно. Совокупность всех обученных элементарных персептронов формирует финальный классификатор. Важно отметить, что поскольку рассматриваемые параметры диаграмм индентирования для двух классов сталей являются разделимыми, то алгоритм Мезарда-Надала для них сходится.

Рисунок 3 – Алгоритм построения классификатора

Так как на каждом его этапе число неверно классифицируемых примеров уменьшается как минимум на 2 – один элементарный персептрон с бинарной активационной характеристикой верно классифицирует как минимум два отличных друг от друга примера. То есть процесс построения такого классификатора является конечным. Аналогичная ситуация наблюдается и для других рассмотренных в работе групп сталей. Для них успешно построены классификаторы по приведённому выше алгоритму.

 Заключение

Рассмотренный подход позволяет для имеющихся образцов попарно отделить друг от друга все исследуемые группы сталей в пространстве признаков, формируемом аппроксимационными коэффициентами диаграмм индентирования. Предложенная схема классификации дает возможность для каждой конкретной экспериментальной диаграммы индентирования выбрать соответствующий определённому типу стали комитет нейронных сетей и вычислить значения механических характеристик. Погрешность определения предела текучести для контрольной серии образцов не превысила 10%, что соответствует техническим требованиям.

1. М.Б. Бакиров, О.А. Мишулина, И.А. Киселев, И.А. Круглов. Исследование возможности восстановления диаграмм деформирования с помощью нейросетевого подхода // Заводская лаборатория. Диагностика материалов, 2010. – Т. 76. №7. – С. 42-48.
2. O.A. Mishulina, I.A. Kruglov, M.B. Bakirov. Neural networks committee decision making for estimation of metal’s hardness properties from indentation data // Optical Memory and Neural Networks (Information Optics), 2011. – Vol. 20. No. 2. – Pp. 132-138.
3. O.A. Mishulina, I.A. Kruglov, M.B. Bakirov. Neural Networks Committee for Improvement of Metal’s Mechanical Properties Estimates / // Lecture Notes in Computer Science. – Springer, 2011. – Vol. 6593. – Pp. 150-157.
4. Тихонов А. Н., Леонов А. С., Ягола А. Г. Нелинейные некорректно поставленные задачи. М.: Наука, 1995.
5. Burger M., Engl H. W. Training neural networks with noisy data as an ill-posed problem // Adv. Comp. Math. 2000. No. 13. Pp. 335–354.
6. Kaltenbacher B., Neubauer A., Scherzer O. Iterative regularization methods for nonlinear ill-posed problems. Walter de Gruyter, 2008.
7. И.А. Круглов, О.А. Мишулина. Нейросетевое моделирование векторной функции многих переменных в условиях плохой обусловленности задачи аппроксимации // Известия РАН. Теория и системы управления, 2013. – № 4. –С. 3-18.
8. Burger M., Neubauer A. Analysis of Tikhonov regularization for function approximation by neural networks // Neural networks. 2003. No. 16. Pp. 79–90.
9. Нужный А. С., Шумский С. А. Регуляризация Байеса в задаче аппроксимации функции многих переменных // Математическое моделирование. 2003. Т. 15, № 9. Стр. 55–63.
10. Kruglov I., Mishulina O., Bakirov B. Quantile based decision making rule of the neural networks committee for ill-posed approximation problems // Neurocomputing. 2012. Vol. 96. Pp. 74–82.
11. Mezard M., Nadal J.-P. Learning in feedforward layered networks: the tiling algorithm // J. Phis. A: Math. Gen. 1989. No. 22. Pp. 2191–2203.

Все статьи автора «Круглов Игорь Александрович»