При имитационном моделировании динамических систем и разработке тренажеров часто управляющие воздействия оператора определяются как центрированные случайные функции (отклонение от программного управления (тренд); воздействия по стабилизации программного движения за вычетом флуктуаций). При их определении по данным нормальной эксплуатации используется итерационная процедура (относится и к определению передаточных функций, как оператора, так и объекта). Модели человека-оператора соответствуют моделям отдельных органов (обычно вход – восприятие; выход – движение конечностей). Часто человек-оператор действует в импульсном режиме; прогнозирование производится в результате распознавания образов; в течение каждого периода времени использует максимальное управляющее воздействие. Определение динамических характеристики системы в процессе функционирования системы на основе реакций объекта на периодические импульсные сигналы оператора. Реакцию системы человек-оператор оценивает по концептуальной модели.
Рассматриваемые эргатические системы описываются уравнениями вида
,
,где 
- векторы фазовых координат, управляющих и возмущающих воздействий; 
- матрицы соответствующих размерностей, 
- вектор-столбец постоянных времени. Управляющие воздействия оператора рассматриваются как непрерывные функции 
, удовлетворяющие условиям:
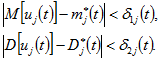
Стиль управления по каждому из каналов определяется параметрами внутренней структуры случайной функции (управляющее воздействие первого приближения)
,
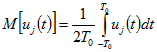
(зависит от выбора интервала усреднения 
; выбор значения 
должен быть согласован со значением доминирующей в 
частоты 
; 
; обычно принимается 
). Удобным оказалось рассмотрение управляющих воздействий как узкополосный случайный процесс; оценка оператором характеристик объекта управления, вид и структура управляющих воздействий существенно зависят от собственных частот колебаний 
и безразмерных коэффициентов демпфирования 
(собственных чисел 
матрицы 
).
В ряде случаев целесообразно рассмотрение управляющих воздействий оператора как импульсных процессов. В этом случае в качестве основных характеристик управляющих воздействий рассматриваются амплитуды, длительности и вероятности их распределения. Отметим интересный факт: распределение случайных амплитуд 
импульсов не является нормальным, хотя дискретные значения 
распределены нормально.
При качественной оценки связи между стимулом и реакцией оператора предполагается, что неперекрывающимся импульсам выходной координаты объекта соответствуют неперекрывающиеся импульсы управляющих воздействий. Однако, в силу инерционности объекта и оператора, а также случайных внешних возмущений и внутренних помех управляющие воздействия и изменения выходных координат представляют собой серии перекрывающихся импульсов. Поэтому установление связи между стимулом и реакцией по данным нормальной эксплуатации порою затруднительно.
Управляющие воздействия нередко рассматриваются как выбросы. Здесь параметры управляющих воздействий определяются как некоторые числовые характеристики, рассматривая выбросы случайного процесса 
. В качестве параметров управляющих воздействий рассматриваются числа 
и длительности 
положительных и отрицательных выбросов, а также их средние значения 
на интервале 
.
Если сигналы 
и 
являются гауссовыми и имеют нулевое среднее значение, то нормированная взаимно-корреляционная функция имеет вид
и выражается через знаковую взаимно-корреляционную функцию 
. Она получается из
заменой 
на 
:
.При решении задач, где требуется выявить максимум коэффициента корреляции, знаковая корреляционная функции более предпочтительна. Правда, среднеквадратичное значение случайных сигналов при использовании знаковой корреляции может быть определено лишь при добавлении к 
специальных вспомогательных сигналов.
Имеют место следующие формулы:
Если 
, то 
являются независимыми при данном 
.
Алгоритм вычисления знаковой корреляционной функции совершенно аналогичен алгоритму вычисления корреляционной функции.
Близость статистической связи между 
и 
стационарного процесса к линейной функциональной зависимости:
оценивается по 
; чем ближе 
к 1 , тем более определенна связь между 
и 
и наоборот.
При 
(на приведенном рисунке) при помощи уравнения 
можно с большей степенью достоверности предсказать 
по 
, чем по уравнению 
при 
.
Преимущество использования знаковой корреляционной функции перед другими состоит в простоте использования, наглядности и интерпретации. Поэтому она широко использовалась при составлении когнитивной модели транспортной эргатической системы [1…6].
Библиографический список
- Тюкалов Д.Е., Данилов А.М. Моделирование и подготовка операторов транспортных эргатических систем / Молодой ученый. – 2015. – № 3 (83). – С. 247-249.
- Петренко В.О., Данилов А.М. Управление в пространстве: идентификация управляющих воздействий / Современные научные исследования и инновации. – 2014. – № 12-1 (44). – С. 146-149.
- Тюкалов Д.Е., Данилов А.М. Формирование критериев динамического подобия модели реальному объекту/ Молодой ученый. – 2015. – № 4 (84). – С. 278-280.
- Данилов А.М., Пылайкин С.А. Оценка параметров распределения амплитуд в управляющих движениях оператора / Молодой ученый. – 2013. – № 3. – С. 48-52.
- Нугаев А.С., Данилов А.М. Параметры распределения управляющих воздействий оператора в эргатической системе / Молодой ученый. – 2014. – № 19. – С. 228-231
- Будылина Е.А., Гарькина И.А., Данилов А.М., Пылайкин С.А.Аналитическое определение имитационных характеристик тренажных и обучающих комплексов / Фундаментальные исследования. – 2014. – № 6-4. – С. 698-702.