Введение

Одним из ключевых вопросов логистики является выбор оптимальных кольцевых маршрутов передвижения материальных потоков, которые могут минимизировать стоимость доставки товара потребителям. Их определение при доставке товара с нескольких баз представляется довольно сложной задачей дискретной оптимизации, которая рассмотрена лишь для некоторых частных случаев. Обзор некоторых подходов к ее решению приведен, например, в [1]. Из них наибольший интерес представляет использование метода ветвей и границ (ВиГ), так как он является точным по сравнению со всеми другими. Он основан на глобальном поиске решения и, следовательно, обладает способностью избежать «ловушек» при применении методов локальной оптимизации. Его возможности постоянно расширяются [2]. Разработан усовершенствованный алгоритм ВиГ, позволяющий посещать пункты разгрузки товара несколько раз [3]. Следует заметить, что для неполного транспортного графа он может иметь вырождение решения [4].

Модель и метод расчета

Постановка задачи заключается в следующем. Базы Б1 и Б2 расположены в противоположных наиболее удаленных концах транспортной сети. Известна матрица стоимости переезда между вершинами транспортного графа. Грузоподъемность не ограничена. Требуется найти кольцевые маршрута движения с каждой базы минимальной суммарной стоимости.
Решение состоит из двух основных этапов. На первом этапе находим оптимальные кольцевые маршруты из условия, чтобы их суммарная стоимость была наибольшей. Для этого решаем задачу коммивояжера, используя метод фиктивных узлов и ветвей [3].
Алгоритм вычислений на первом этапе заключается в следующем.

1. В исходной матрице заменяем стоимость каждой ветви  приведенной ее величиной

, (1)

где: 

 –  наибольшее значение стоимости в исходной таблице.

2. Вводим внешние фиктивные узлы в вершины, дублирующие базы.

3. Соединяем базы и фиктивные узлы со смежными вершинами ориентированными дугами. При этом их направление противоположное.

4. Соединяем базы и дублирующие фиктивные узлы четырьмя фиктивными ветвями: Ф1-Ф3 и Ф3-Ф2, Б2-Ф4 и Ф4-Б1, чтобы получился замкнутый круг. Их длина принимается не менее минимальной величины хорды в рассматриваемой базе. Принципиальная схема организации двух колец представлена на рис. 1.

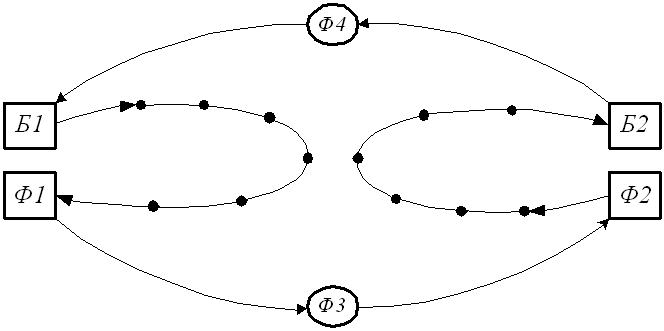
Рис. 1. Схема ввода внешних фиктивных узлов

5. Составляем расчетную матрицу стоимости с учетом введенных внешних фиктивных узлов.

6. Выполняем операции приведения по строкам и столбцам с помощью наименьших их элементов.

7. Производим оценку элементов матрицы.

8. Удаляем из матрицы ветвь с наибольшей оценкой и блокируем движение в обратном направлении. Получаем новую матрицу меньшего размера.

9. Создаем фиктивные матрицы и , вводя в матрицу  вычеркнутые строку и столбец.

10. Выполняем над матрицами ,  и  операции, описанные в пунктах 6-9 до тех пор, пока последняя вычеркиваемая ветвь не станет очевидной.
Оптимальная схема маршрута устанавливается из сравнениявсех возможных полученных рациональных вариантов.
На втором этапе решается задача коммивояжера по критерию минимальной стоимости отдельно каждого полученного кольца. Затем путем обмена смежными вершинами между двумя маршрутами выполняется улучшение решения. Применение разработанной методики рассмотрим на следующем примере.

Пример

Исходная матрица стоимости представлена в табл. 1, где максимальное ее значение составляет 8 единиц. Базы Б1 и Б2 расположены в вершинах 1 и 11, соответственно.

	1	2	3	4	5	6	7	8	9	10	11	12	13	14
1		3	2	1								3
2	3		1		8	6						4	2
3	2	1		2	3	5	5
4	1		2			4	7
5		8	3			8		6	4			5	6	7
6		6	5	4	8		6	3	3	6
7			5	7		6		4		2
8					6	3	4		7	5	7
9					4	3		7			5		2	6
10						6	2	5			6
11								7	5	6				7
12	3	4			5								7
13		2			6				2			7		2
14					7				6		7		2

В табл. 2 представлена расчетная матрица после применения формулы (1) и ввода внешних фиктивных узлов и ветвей. Приведем краткие результаты расчета табл. 2 по вышеизложенному алгоритму. 

Расчетная матрица стоимости Таблица 2

	1	2	3	4	5	6	7	8	9	10	11	12	13	14	Ф1	Ф2	Ф3	Ф4
1		5	6	7								5
2			7		0	2						4	6		5
3		7		6	5	3	3								6
4			6			4	1								7
5		0	5			0		2	4			3	2	1
6		2	3	4	0		2	5	5	2
7			3	1		2		4		6
8					2	5	4		1	3	1
9					4	5		1			3		6	2
10						2	6	3			2
11																		1
12		4			3								1		5
13		6			2				6			1		6
14					1				2		1		6
Ф1																	5
Ф2								1	3	2				1
Ф3																1
Ф4	5

В процессе решения были получены два кольцевых маршрута с максимальной суммарной стоимостью. Если отбросить введенные начальные и расчетные фиктивные узлы, то получаются следующие схемы движения: 1-12-13-5-2-5-6-7-4-7-3-1 и 11-10-8-9-14-11 (рис. 2). Заметим, что вершины 5 и 7 посещаются дважды. Маршруты имеют восемь смежных вершин: 5, 6, 7, 8 , 9, 10, 13 и 14.

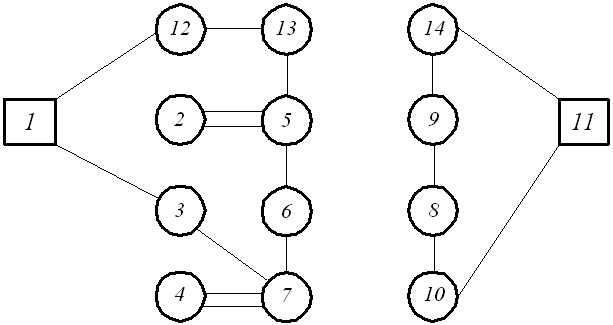
Рис. 2. Определение кольцевых маршрутов на первом этапе

Переходим ко второму этапу и рассматриваем все комбинации сочетаний при обмене их между маршрутами. В результате решения задачи находим две оптимальные схемы движения: 1-4-3-2-3-5-12-1, стоимостью 16 единиц и 11-10-7-8-6-9-13-14-11, стоимостью 29 единиц (рис. 3). Заметим, что вершина 3 посещается дважды.

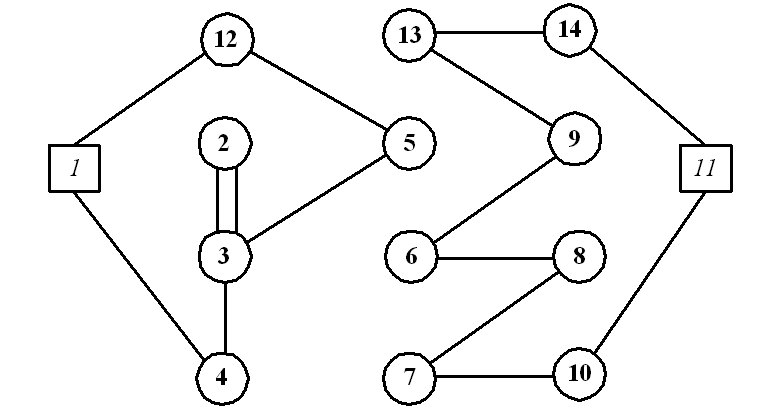
Рис. 3. Оптимальные маршруты.

Выводы

Таким образом, разработана методика нахождения кольцевых маршрутов с двух баз снабжения с использованием метода фиктивных узлов и ветвей.

1. Пожидаев, М.С. Алгоритмы решения задачи маршрутизации транспорта [Текст]: автореф. дис…. канд. техн. наук / М.С. Пожидаев. – Томск, 2010.
2. Костюк Ю. Л. Эффективная реализация алгоритма решения задачи коммивояжера методом ветвей и границ. [Текст] / Ю. Л. Костюк. // Прикладная дискретная математика. – Томск.: Национальный исследовательский Томский государственный университет., 2013.– №2 (20). – С. 78-90.
3. Подшивалова, К.С. Повышение эффективности перевозок мелкопартионных грузов автомобильным транспортом [Текст]: автореф. дис…. канд. техн. наук / К.С. Подшивалова – Волгоград. 2007. – С.16.
4. Подшивалов С. Ф. Особенность использования метода ветвей и границ в задаче маршрутизации при неполном транспортном графе. [Текст] / Подшивалов С. Ф. Подшивалова К. С. // Экономика и математические методы.– М. 2014, том 50, №3, с. 190-196.

Все статьи автора «Подшивалова Кристина Сергеевна»