Решения задач теплопроводности для относительно простых случаев стандартных геометрических тел (стержень, цилиндр, плоскость, сфера, и т.д.) могут быть легко получены аналитически. Однако на практике чаще приходится иметь дело с задачами теплопроводности, которые или не поддаются аналитическим методам решения, или аналитические методы оказываются для них крайне неэффективными. Это может быть связано как со сложной геометрией рассматриваемых объектов, так и с нелинейностью построенных для решения задачи математических моделей (например, учитывающих неоднородность посторонних включений или свойств самого объекта).

В таких случаях применяются универсальные способы решения с использованием компьютера, в качестве которых выступают численные методы. Их программная реализация в относительно простых случаях может быть выполнена самим исследователем на одном из языков программирования. В более сложных случаях может использоваться какая-либо подходящая вычислительная система, например, MathCAD или Matlab.

Большие инженерные задачи обычно требуют специальных математических вычислительных комплексов [1], таких как, например, ANSYS и PHOENICS. Первый из них предназначен для решения различных физических задач (расчет прочности, тепломассообмена, задачи теплофизики, гидрогазодинамики, электромагнетизма, и т.д.). Второй имеет специальную ориентацию на задачи компьютерного моделирования в области динамики жидкости и тепломассообмена.

В представленной работе рассматривается учебная задача о моделировании процесса теплопроводности в плоской неоднородной (составной) пластине, состоящей из нескольких слоев с отличающимися теплофизическими свойствами. Задача может быть использована при обучении студентов основам компьютерного моделирования реальных физических процессов и, в частности, процессов теплопроводности.

Рассмотрим плоскую пластину, состоящую из нескольких слоев. Будем считать, что нижняя сторона пластины теплоизолирована, а остальные поддерживаются при постоянной температуре. Пластина может содержать различные протяженные области, занятые источниками тепла или холода определенной мощности (прямоугольной формы). Рассчитаем распределение температур в пластине в произвольные моменты времени.

Рассматриваемая в такой постановке задача, вообще говоря, является трехмерной, т.к. температура будет изменяться как в плоскости пластины (вдоль осей x и y), так и по ее толщине (по оси z). Однако изменениями температуры по оси z можно пренебречь, если пластина достаточно тонкая, ее теплопроводность велика, а коэффициенты теплоотдачи на верхней и нижней поверхностях относительно малы [1]. Будем считать, что для нашей пластины перечисленные условия выполнены и поэтому температурное поле будет двумерным.

Для решения задачи запишем дифференциальное уравнение теплопроводности:

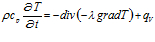,                 (1)

где , .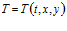

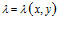Для двумерного случая уравнение (1) перепишется в виде

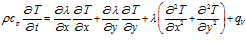.            (2)

В случае необходимости теплообмен с окружающей средой через верхнюю и нижнюю поверхности пластины можно имитировать внутренним стоком теплоты:

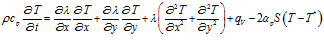,        (3)

где 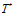– температура окружающей среды, 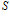– площадь верхней (нижней) поверхности пластины, 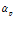– коэффициент теплоотдачи.

В случае стационарного (установившегося) процесса уравнение теплопроводности (2) перепишется в виде:

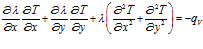.            (4)

На основе (4) можно рассчитать температурное поле в пластине для стационарного случая.

Для численных расчетов будем использовать уравнение (2). Перепишем его в конечно-разностной схеме:

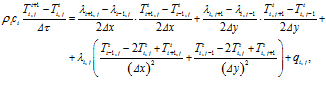
откуда

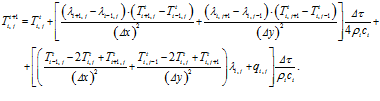        (5)

На основе (5) решим задачу о распределении температур в пластине, состоящей из набора слоев.

Моделирование рассматриваемого процесса выполнено в компьютерной программе, написанной в среде визуального программирования Delphi. Для ускорения работы с изображением при разработке программы использовано свойство битовой карты TBitMap – ScanLine [2, 3], представляющее собой массив указателей на строки с данными битовой карты (строки точечного изображения).

Программа позволяет задавать размеры области моделирования (прямоугольной пластины), параметры материала слоев пластины и их размер, мощности источников тепла или холода. Распределение источников тепла (холода) в пластине задается путем выделения мышью областей на пластине.

На рис. 1-2 рассмотрены последовательные этапы моделирования в случае пластинки размером 36×36 см. Пластинка состоит из трех слоев: олово (ширина 15 см), алюминий (ширина 12,5 см) и медь (ширина 8,5 см). Начальные параметры металлов [4], из которых состоят слои пластины, взяты при температуре около 293 К: олово – 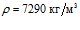, , 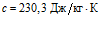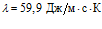; алюминий – 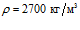, , 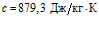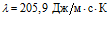; медь – 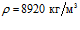, , 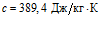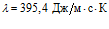. Отметим, что параметры металлов изменяются в зависимости от температуры.

Для случая, представленного на рис. 1 на пластинке расположены два источника тепла 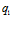и 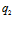прямоугольной формы (15×5 см и 5×8 см) с отличающимися мощностями 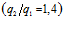. Моменты времени: а) t=3 с, б) а) t=8 с, в) t=22 с, г) t=42 с, д) t=68 с, е) t=128 с.

Для случая, представленного на рис. 2 на пластинке расположен источник тепла 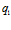и источник холода 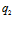прямоугольной формы (15×5 см и 5×5 см) с отличающимися мощностями 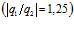. Моменты времени: а) t=3 с, б) а) t=7 с, в) t=20 с, г) t=34 с, д) t=55 с, е) t=108 с. Видно, что источник тепла постепенно нагревает слои пластины и уменьшает область низких температур, образованных источником холода.

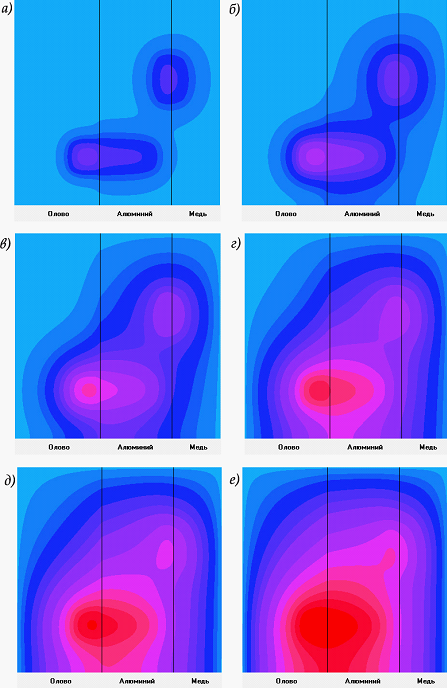
Рисунок 1. Распределение температур в пластине в случае двух источников тепла

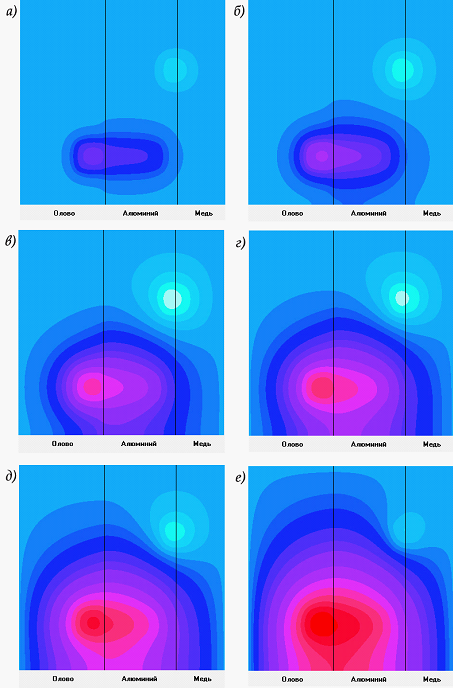
Рисунок 2. Распределение температур в пластине в случае источников тепла и холода

Материал, изложенный в статье, будет интересен и полезен студентам физико-математических специальностей. На основе него могут быть проведены численные эксперименты в следующих направлениях: изучение влияния коэффициента теплоотдачи на распределение температур в пластине; изучение влияния свойств материала пластины и свойств отдельных включений на распределение температур в пластине; исследование температурных режимов стен зданий при различных погодных изменениях температуры; решение задачи об определении температуры в центральной части пластины на основе значений температур ее поверхностей, и т.д.

1. Солодов А.П. Тепломассообмен в энергетических установках. [Электронный ресурс]. – Режим доступа: http://twt.mpei.ac.ru/solodov/HMT-eBook_2009/index.htm
2. Дмитриев В.Л. Модификация LSB-метода на основе последовательностей особенных точек изображения // Отраслевые аспекты технических наук. 2013. № 12. – С. 17-20.
3. Дмитриев В.Л. Защита сетевых публикаций на основе динамически изменяющихся изображений // Отраслевые аспекты технических наук. 2014. № 6. – С. 15-19.
4. Дмитриев В.Л. Элементы линейной акустики. – Уфа: РИЦ БашГУ, 2008. – 85 с.

Все статьи автора «Дмитриев Владислав Леонидович»