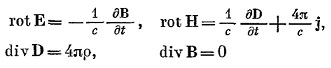Введение.
Математическая безупречность любой теории ничего не говорит об истинности этой теории. Вот как об этом, применительно к геометрии, пишет Г. Рейхенбах [1 с.22]:
«Если математик не связан использованием определенной системы аксиом и может применять аксиому не-а точно так же, как и аксиому а, тогда утверждение а не относится к математике, а математика есть не что иное, как наука об импликациях, то есть об отношениях типа «если …, то …». Следовательно, для геометрии как математической науки не существует проблемы истинности ее аксиом … Аксиомы не являются ни истинными, ни ложными, а лишь произвольными утверждениями».
Теория относительности построена чисто математически на двух постулатах (аксиомах или принципах), поэтому, если мы считаем эти постулаты верными, то нам не остается ничего другого, как признать верной и всю теорию. Давайте внимательнее присмотримся к этим постулатам. Как известно, они взаимно противоречивы, но их противоречивость устраняется допущением относительности времени. Вот как об этом писал Эйнштейн [2 с.418]:
«Оказывается, что принцип постоянства скорости света и принцип относительности противоречат один другому только до тех пор, пока сохраняется постулат абсолютного времени, т.е. абсолютный смысл одновременности. Если же допускается относительность времени, то оба принципа оказываются совместимыми; в этом случае, исходя из этих двух принципов, получается теория, называемая «теорией относительности».
Таким образом, принцип относительности времени, так сказать, «склеивает» исходно несовместимые постулаты теории относительности. При этом у релятивистского физического времени появляются две очень интересные особенности. Первая – это его замедление на движущихся телах, вторая – это относительность одновременности.
Релятивистское замедление времени – методологический эффект?
Как известно, согласно теории относительности, в движущейся системе отсчета, по сравнению с неподвижной, время замедляется [2 с.185; 3 с.250]. Это следствие вытекает из сравнения промежутков физического (в формулировке Эйнштейна [2 с.149-150]) или собственного (в формулировке Борна [3 с.244]) времени этих систем отсчета, между двумя одними и теми же пространственно-временными событиями. Причем эти пространственно-временные события выбираются таким образом, что в неподвижной системе отсчета эти события происходят в разных пространственных точках, а в движущейся – в одной и той же. То есть время в неподвижной системе отсчета измеряется парой разноместных часов этой системы, а в движущейся системе – ее единственными часами, и потом эти измерения сравниваются. Нетрудно заметить, что условия проведения измерений в разных системах отсчета различны. Причем известно, что именно этому различию обязано своим происхождением утверждение о замедлении времени в движущейся системе отсчета [4 с.23], и только ему. Очень доступно данный факт был описан доктором физико-математических наук, профессором физического факультета МГУ в его работе «Выражение общих свойств физических процессов в пространственно-временной метрике специальной теории относительности» [5 с. 644], цитата:
«В действительности в специальной теории относительности речь идет о сопоставлении интервала времени, прошедшего в одной точке какой-либо системы отсчета, с разностью времен, прошедших в разных точках другой системы отсчета… Взятые в единственном числе часы в определенной точке какой-либо системы отсчета, всегда отстают от совместных показаний пары синхронизированных часов другой системы».
Действительно, если для сравнения отрезков времени, прошедших в разных системах отсчета, выбрать пару событий, таких, что в неподвижной системе отсчета они будут фиксироваться единственными часами (события происходят в одной и той же точке неподвижной системы отсчета), а в движущейся системе отсчета – парой часов, то разность показаний двух часов движущейся системы отсчета будет больше, чем разность показаний одних и тех же покоящихся. То есть в данном случае получаем, что время в движущейся системе идет быстрее, а не медленнее. Здесь можно услышать возражение, что с точки зрения неподвижного наблюдателя разноместные часы движущейся системы отсчета идут не синхронно, поэтому такое сравнение не является корректным. Но ведь физическое время в движущейся системе отсчета это время движущегося вместе с этой системой наблюдателя, для которого все ее часы синхронны. Движущийся наблюдатель имеет полное право измерять время в своей системе отсчета по разноместным часам.
Если мы запрещаем наблюдателю какой-либо системы отсчета пользоваться разноместными часами, то, во-первых, вступаем в противоречие с эйнштейновским определением физического времени, как множества синхронизированных часов данной системы отсчета, цитата [2 с.150]:
«Пусть даны две системы координат S и S′, движущиеся равномерно и прямолинейно одна относительно другой. Предположим, что с каждой из этих двух систем связана группа часов, причем все часы, принадлежащие к одной и той же системе, идут в фазе. В этих условиях показания группы часов, связанной с S, определяют физическое время по отношению к системе отсчета S; подобным же образом показания группы часов, связанной с системой отсчета S′, определяют физическое время по отношению к S′».
А во-вторых, как уже подчеркивалось ранее, мы ставим наблюдателей в заведомо неравные условия при проведении измерений.
Если же мы уравняем условия проведения измерений, т.е. сделаем их идентичными, то получим равенство темпов хода времени в движущихся друг относительно друга системах отсчета, что наглядно показано в приведенном далее примере встречно летящих ракет.
Пусть в голове и хвосте двух идентичных ракет A и B, имеющих собственную длину L0, закреплены идентичные синхронизированные часы. Ракеты сближаются со скоростью V, двигаясь по инерции вдоль соединяющей их прямой. При встрече ракет сначала совмещаются их головные часы, а потом хвостовые. Назовем пространственно-временную точку встречи головных часов ракет – событием X, а точку встречи хвостовых часов – событием Y. Найдем, отличаются ли темпы хода физического времени ракет, измерив отрезки времени между событиями X и Y по часам каждой из ракет. По часам ракеты А, учитывая, что в результате Лоренцева сокращения длина ракеты В меньше и равна L, события X и Y разделены отрезком времени:
∆tA = (L0 + L)/V
Аналогично по часам ракеты В те же события разделены отрезком времени:
∆tB = (L0 + L)/V
Оба эти отрезка совпадают по величине, что с очевидностью следует не только из приведенных выше равенств, но и из соображений симметрии. Сравнив полученные значения отрезков времени, пилоты ракет убедятся, что один и тот же интервал XY имеет одинаковую длительность как по часам ракеты А, так и по часам ракеты В, значит темп хода физического времени на ракетах одинаков.
В качестве еще одного примера, подтверждающего неоднозначность «стандартной» релятивистской методики сравнения темпов хода часов, можно привести следующий. Пусть имеется неподвижная кольцевая железная дорога сколь угодно большого радиуса. По этой дороге по инерции движется поезд. Учитывая, что кривизна дороги сколь угодно мала, – система отсчета, связанная с поездом, на конкретном небольшом участке пути, сколь угодно близка к инерциальной системе отсчета; пассажир поезда, сравнивая показания единственных часов на дороге с парой часов на своем поезде, получит, что часы на дороге идут медленнее. Однако в данном случае это не верно [6 с.200, 7 с.309].
Относительность одновременности и принцип причинности.
С точки зрения наблюдателя какой-либо инерциальной системы отсчета часы в точках A и B, неподвижных в этой системе отсчета, идут синхронно, если разность τB2 – τA1, времени прихода светового сигнала в точку B (по часам B) и времени испускания светового сигнала из точки A (по часам A) равна разности τ′A2 – τ′B1, времени прихода светового сигнала в точку A (по часам A) и времени испускания светового сигнала из точки B (по часам B) [2 c.417]. При этом предполагается, что скорости распространения сигналов, посылаемых из точки A в точку B и обратно, равны. Причем в рамках данной неподвижной системы отсчета это правило справедливо как в теории относительности Эйнштейна, так и в классической механике Галилея-Ньютона. Действительно, согласно классической механике, скорости распространения сигналов в обоих направлениях (от точки A к B и от точки B к A) складываются со скоростью источника, но в системе отсчета, где и источник, и приемник неподвижны – скорости этих сигналов равны.
С точки зрения движущегося относительно этих часов наблюдателя (согласно специальной теории относительности) скорость света остается неизменной, и поэтому времена распространения сигналов от точки A к B и от точки B к A в общем случае уже не равны, что и дает этому наблюдателю основание считать часы в точках A и B несинхронными. Данный эффект называется релятивистской «относительностью одновременности». Согласно же классической механике, скорости световых сигналов «туда» и «обратно» складываются со скоростью системы отсчета, поэтому времена распространения сигналов от точки A к B и от точки B к A остаются для наблюдателя равными, что означает синхронность часов в точках A и B для наблюдателя. Хотя заключения движущегося наблюдателя о синхронности часов в точках A и B с позиций классической механики и с позиций специальной теории относительности различны, тем не менее, оба эти заключения не противоречат причинной теории времени, т.к. в обоих случаях использованные определения метрической одновременности пространственно разделенных событий вполне согласуются с топологической одновременностью, что подробно рассмотрено в [8 с.447-462].
Как уже упоминалось выше, часы, синхронные в собственной инерциальной системе отсчета, где они неподвижны, – с точки зрения движущегося относительно них со скоростью V наблюдателя (согласно теории относительности) в общем случае идут не синхронно. Это означает, что часы в точках A и B показывают разное время, отличающееся на величину ∆t0, которая дается выражением [9 с.17; 10 с.68-69; 11 с.62]:
∆t0 = γ∙V∙Δx/c2
где: γ = (1 – V 2/c2) –1/2 – Лоренц-фактор; Δx – проекция расстояния между часами в системе отсчета наблюдателя на прямую, параллельную скорости V; с – скорость света.
В системе отсчета этого наблюдателя, вследствие Лоренцева сокращения, величина Δx в γ раз меньше величины Δx0, представляющей собой проекцию расстояния между часами на прямую, параллельную скорости V, но в системе отсчета, где эти часы неподвижны. Поэтому предыдущее уравнение эквивалентно следующему:
∆t0 = V∙Δx0/c2 (1)
Причем, для наблюдателя отстают (показывают меньшее на ∆t0 время) часы, движущиеся с его точки зрения впереди.
Исследуем ход неподвижных часов с точки зрения движущегося наблюдателя, при изменении им своей скорости (т.е. при его переходе в другую инерциальную систему отсчета). Пусть в неподвижной системе отсчета в точках A и B, расстояние между которыми равно Δx0, расположены идентичные и синхронные часы. Наблюдатель движется вдоль прямой AB с постоянной скоростью V. Причем вначале он находится за границами отрезка AB и в процессе своего движения первыми встречает часы в точке B (рис. 1).
Рис. 1. Наблюдатель начинает и заканчивает разворот в непосредственной близости от точки B внутри отрезка AB, поэтому при совмещении с часами B он покоится в соответствующей инерциальной системе отсчета.
В момент первого совмещения с точкой B наблюдатель фиксирует на часах B время t1. С точки зрения наблюдателя, в этот момент часы в точке A опережают часы в точке B, и согласно (1), имеют следующие показания:
τ1 = t1 + V∙Δx0/c2
Сразу после встречи с часами B наблюдатель включает двигатели и разворачивается, путем торможения и последующего разгона в обратную сторону с постоянным ускорением a. Когда на обратном пути, непосредственно перед повторной встречей с точкой B, он достигает скорости –V, то выключает двигатели и продолжает двигаться по инерции. После этого, при совмещении с точкой B, наблюдатель фиксирует на часах B время t2. Теперь для него часы в точке A отстают от часов в точке B, и согласно (1), имеют следующие показания:
τ2 = t2 – V∙Δx0/c2
Сколько времени с точки зрения наблюдателя прошло по часам A пока он разворачивался? Чтобы найти это время вычтем показания часов A перед разворотом из их показаний после разворота, в результате получим:
τ2 – τ1 = t2 – t1 – 2∙V∙Δx0/c2
Заметим, что t2 – t1 это время разворота наблюдателя по часам B, т.е. время, которое затратил наблюдатель на разворот с точки зрения неподвижной системы отсчета, в которой отрезок AB покоится. Учитывая, что ускорение наблюдателя в неподвижной системе отсчета постоянно, это время равно:
t2 – t1 = 2∙V/a
Подставляя полученное значение в предыдущее уравнение, получим:
τ2 – τ1 = 2∙V/a – 2∙V∙Δx0/c2
Если при этом выполняется неравенство:
2∙V/a < 2∙V∙Δx0/c2,
то τ2 < τ1, и значит, с точки зрения наблюдателя, пока он разворачивался – часы A шли вспять. Проверим, может ли полученное нами неравенство быть истинным. Преобразовав его получим:
a∙Δx0/c2 > 1
Очевидно, что при достаточно большой величине a и/или Δx0, это неравенство будет истинно. Оценим при каких значениях a и Δx0 выражение a∙Δx0/c2 будет равно единице. Пусть ускорение a равно 106 м/с2, что примерно соответствует ускорению пули в стволе огнестрельного оружия, тогда:
Δx0 ≈ 9∙1010 м. = 90 млн. км.
Это меньше чем расстояние от Солнца до Земли. То есть с точки зрения пули, выпущенной на Земле, пока она летела в стволе – время на Солнце, согласно теории относительности, шло вспять.
Таким образом, мы получили, что если в точке A находится какое-либо физическое тело, и с ним происходит причинно-связанная последовательность событий, такая, что событие X1, произошедшее в момент времени τ1 является причиной события X2, произошедшего в момент времени τ2, то с точки зрения наблюдателя, событие X1 может произойти позже X2 (τ2 < τ1). Иначе говоря, хотя релятивистское определение метрической одновременности пространственно разделенных событий и не противоречит топологической одновременности событий в разных точках A и B, однако заставляет наблюдателя считать, что при его развороте причинная последовательность событий, происходящих с одним и тем же телом в точке A, нарушается, что вряд ли может соответствовать действительности [1 с.156-163]. Вот что пишет, например, А.И. Жуков в своей книге «Введение в теорию относительности» по поводу возможности нарушения принципа причинности [12 с.30]:
«Никакое явление не может произойти раньше своей причины. Этот закон не допускает никаких исключений; если какая-либо теория приходит с ним в противоречие, то это для нее является смертельным приговором».
Здесь мы можем услышать возражение, что при развороте – для наблюдателя меняется не «реальная» последовательность причинно-связанных событий в точке A, а меняется «соглашение об одновременности», которое и заставляет наблюдателя считать, что последовательность этих событий изменилась. Но тогда релятивистское «соглашение об одновременности», которое приводит наблюдателя к такому заключению, нуждается в пересмотре. В подтверждение сказанного приведем далее простой мысленный эксперимент.
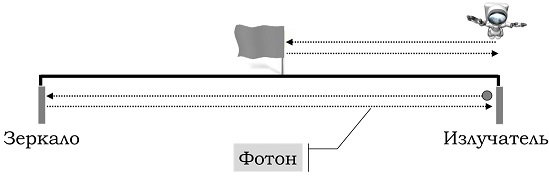
Пусть имеется неподвижный жесткий стержень. На одном конце этого стержня расположен излучатель фотонов, а на другом – зеркало. Вдоль прямой, на которой лежит этот стержень, движется наблюдатель, его скорость равна половине скорости света. Наблюдатель подлетает к стержню со стороны излучателя. Когда наблюдатель и излучатель совмещаются, то излучатель испускает в сторону зеркала фотон. Фотон летит до зеркала, отражается от него и возвращается к излучателю. Наблюдатель летит ровно до середины стержня, которая отмечена флажком, быстро разворачивается и летит обратно к излучателю с прежней скоростью (Рис.2). Для простоты условимся, что ускорение наблюдателя при развороте сколь угодно велико. Это позволит нам не учитывать время, затраченное наблюдателем на разворот.
По условию, скорость наблюдателя в 2 раза меньше световой, и расстояние, которое преодолевает наблюдатель, тоже в 2 раза меньше, чем расстояние, которое преодолевает фотон. Значит, наблюдатель и фотон по возвращении встретятся у излучателя. То есть вернутся к излучателю одновременно.
Посмотрим теперь на этот мысленный эксперимент глазами нашего наблюдателя. Хотя наблюдатель не может непосредственно видеть положение фотона относительно стержня, но он всегда может рассчитать это положение. Давайте проделаем этот несложный расчет вместе с ним.
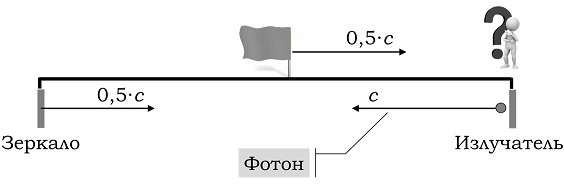
Сначала найдем положение фотона с точки зрения наблюдателя, не за долго до встречи наблюдателя с флажком. С точки зрения наблюдателя – он покоится, а стержень движется относительно него со скоростью, равной половине скорости света. Когда излучатель совмещается с наблюдателем – в сторону зеркала испускается фотон (Рис.3).
Так как согласно теории относительности с точки зрения наблюдателя скорость фотона неизменна, а зеркало движется навстречу фотону со скоростью, равной половине скорости света, то скорость сближения фотона и зеркала составляет полторы скорости света, т.е. в три раза больше скорости сближения наблюдателя и флажка, которая равна половине скорости света. Расстояние же между фотоном и зеркалом только в два раза больше расстояния между наблюдателем и флажком. Следовательно, фотон и зеркало встретятся раньше, чем наблюдатель и флажок, значит, фотон отразится от зеркала еще до встречи наблюдателя с флажком. Пусть, для наглядности, зеркало сразу же после отражения фотона самоликвидируется (взрывается). Тогда наблюдатель уверен, что зеркало разбилось еще до его встречи с флажком.
Теперь посмотрим, где же должен находиться фотон с точки зрения наблюдателя уже после разворота. Сразу после разворота наблюдатель опять вправе считать себя неподвижным. Относительно него стержень движется, но уже в обратную сторону. Теперь излучатель приближается к наблюдателю со скоростью, равной половине скорости света. И фотон, если он уже отразился, тоже приближается к наблюдателю (Рис.4).
Наблюдатель считает, что фотон движется со скоростью света, поэтому фотон приближается к наблюдателю в два раза быстрее, чем излучатель. Для того, чтобы фотон и излучатель встретились одновременно около наблюдателя – расстояние между фотоном и наблюдателем тоже должно быть в два раза большим, чем между излучателем и наблюдателем, но это невозможно. Если фотон уже отразился, то расстояние между ним и наблюдателем будет даже меньше, чем между излучателем и наблюдателем. Следовательно, фотон еще не мог отразиться. То есть сразу после разворота, когда наблюдатель перестал испытывать что-то похожее на гравитационное поле, зеркало с его точки зрения должно быть еще цело, иначе фотон и излучатель прибудут к нему не одновременно.
Таким образом, опираясь только на постулат о постоянстве скорости света, наблюдатель уверен, что до его встречи с флажком зеркало уже разбито, однако после встречи с флажком, на том же основании он уверен, что зеркало еще цело. Это может быть только в том случае, если зеркало в нарушение принципа причинности само собралось из осколков.
Синхронизация часов на ободе вращающегося диска.
Как мы уже отмечали ранее, «время» и «одновременность» в теории относительности являются ключевыми понятиями, обеспечивающими целостность и непротиворечивость ее аксиом, но эти понятия уже не являются самостоятельными, они определяются с помощью еще более фундаментального для этой теории понятия – синхронно идущих часов. Вот цитата из первого тома собрания сочинений Эйнштейна, где он об этом пишет [2 с.10]:
«Таким образом, пользуясь некоторыми (мысленными) физическими экспериментами, мы установили, что′ нужно понимать под синхронно идущими, находящимися в различных местах покоящимися часами, и благодаря этому, очевидно, достигли определения понятий: «одновременность» и «время». «Время» события – это одновременное с событием показание покоящихся часов, которые находятся в месте события и которые идут синхронно с некоторыми определенными покоящимися часами, причем с одними и теми же часами при всех определениях времени».
Способов синхронизации часов можно придумать множество, но каждый из них должен удовлетворять требованию симметрии. Вот фрагмент стр. 148 первого тома собрания сочинений Эйнштейна, где описано это важнейшее и по сути единственное требование к процедуре синхронизации [2 с.148]:
«Для того, чтобы получить полное физическое определение времени, необходимо сделать еще один шаг. Надо сказать, каким образом все часы были выверены в начале эксперимента. Поступим следующим образом: во-первых, найдем способ передавать сигналы, например, из A в B или из B в A. Этот способ должен быть таким, чтобы мы были абсолютно уверены, что явления передачи сигналов из A в B нисколько не отличаются от явлений передачи сигналов из B в A. В этом случае очевидно, что существует только одна возможность поставить часы в точке B по часам в A так, чтобы сигнал, идущий из A в B, проходил бы этот путь за то же время, измеренное с помощью этих же часов, что и сигнал, идущий из B в A».
Как следует из цитаты, условия распространения сигналов, посылаемых от часов A к часам B и обратно, должны быть абсолютно идентичны. Только уверенность в этом дает нам право считать, что времена движения сигналов «туда» и «обратно» равны, и позволяет правильно выставить время на часах B в соответствии с формулой:
τB = τA + ∆τ/2 (2)
где τA – время отправления сигнала по часам A; τB – время отражения сигнала по часам B; ∆τ – время распространения сигнала «туда» плюс «обратно», измеренное единственными часами A.
Здесь следует отметить, что требование идентичности условий распространения сигналов синхронизации «туда» и «обратно», и, как следствие, равенство соответствующих времен – не является каким-то нововведением теории относительности, оно очевидно вытекает из логических соображений и не вызывает никаких сомнений. Однако, в теории относительности, это справедливо только для наблюдателя, неподвижного относительно синхронизируемых часов. Если для пассажира движущейся ракеты часы на ракете идут синхронно, то для неподвижного наблюдателя «головные» часы этой ракеты отстают от ее «хвостовых» часов (см. формулу (1)).
Рассмотрим теперь проблему синхронизации стандартных (т.е. одинаковых) часов, закрепленных на ободе вращающегося диска. Теория относительности утверждает, что непротиворечиво синхронизировать их невозможно, хотя темп хода всех таких часов одинаков [4 с.329, 7 с.311]. Вот как об этом пишет Л. Мардер на стр. 194-195 в своей книге «Парадокс часов» [13 с.194]:
«Пусть на карусели находится (и вращается вместе с ней) большое число стандартных часов C1, C2, …, Cn, закрепленных на равных расстояниях друг от друга по ее круговой кромке. Радиус такой окружности равен r, а угловая скорость вращения карусели – ω; тогда множитель, описывающий замедление хода каждых таких часов с точки зрения системы S, будет равняться (1 – r2ω2)1/2. Однако если пассажир карусели попытается синхронизовать друг с другом последовательно все эти часы, основываясь на эйнштейновской методике, у него ничего не получится. Пусть он синхронизует C2 с C1, потом C3 с C2 и т.д. по всей окружности. Когда он дойдет до часов Cn, то обнаружит, что они будут рассинхронизованы с соседними часами C1».
Мардер не уточняет каким именно способом синхронизируются часы. Не делает он этого видимо потому, что в теории относительности обычно применяется один и тот же, так сказать, «стандартный» способ. Он заключается в том, что часы при синхронизации обмениваются световыми сигналами вдоль соединяющего их отрезка прямой [4 с.329, 7 с.311].
Результат, полученный пассажиром карусели, подтвердит и неподвижный наблюдатель, иначе они пришли бы к противоречию в суждении о синхронности часов C1 и Cn, находящихся в одной точке (Рис. 5). Действительно, с точки зрения неподвижного наблюдателя часы C2 отстают от часов C1, т.к. являются «головными» для движущегося отрезка C1C2, соответственно C3 отстают от C2, C4 отстают от C3 и т.д., следовательно, часы Cn отстают от часов C1.
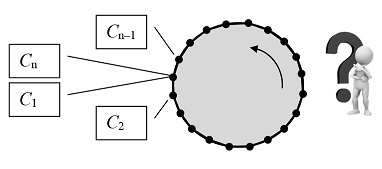 Рис. 5. Часы на ободе диска и «относительность одновременности».
Рис. 5. Часы на ободе диска и «относительность одновременности».
Мы видим, что «стандартная» релятивистская процедура синхронизации часов на ободе вращающегося диска не является транзитивной. Кроме того, как будет показано далее, она не является и симметричной.
Докажем, что часы на ободе вращающегося диска синхронизировать можно. Сделаем так. Синхронизируем все часы на ободе диска до начала его вращения. После этого раскрутим диск, и зададим себе вопрос – синхронно ли теперь идут часы? В процессе раскрутки все часы находились в абсолютно равных условиях в силу круговой симметрии диска, причем как с точки зрения неподвижного наблюдателя, так и с точки зрения пассажира диска. Следовательно, что бы не влияло на ход часов, – это влияние будет идентичным для всех часов. Значит и после раскрутки диска все часы на его краю останутся синхронными, как для неподвижного наблюдателя, так и для пассажира диска. Иными словами, все часы на краю диска равноправны, поэтому, как для неподвижного наблюдателя, так и для пассажира диска, не существует причины, по которой какие-либо часы могли бы уйти вперед или назад по отношению к любым другим. То есть, как с точки зрения наблюдателя на диске, так и с точки зрения неподвижного наблюдателя, все часы на краю диска, после его раскрутки, могут идти только синхронно.
Рассмотрим теперь синхронизацию часов на ободе уже вращающегося диска. Соединим часы A и B световодом, проложенным от часов A вдоль радиуса диска к его центру, и далее от центра вдоль радиуса диска к часам B (рис. 6).
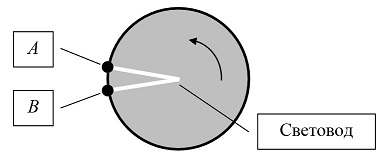 Рис. 6. Часы на ободе диска, соединенные световодом.
Рис. 6. Часы на ободе диска, соединенные световодом.
Время движения светового сигнала от A к B складывается из двух промежутков: времени движения от точки на ободе диска до его центра, и времени движения от центра диска к точке на ободе. В силу круговой симметрии диска, время движения светового сигнала обратно, от B к A, складывается точно из таких же промежутков, поэтому время распространения светового сигнала от A к B равно времени его распространения обратно. Таким образом, чтобы часы B и A были синхронны, требуется просто подвести часы B так, чтобы выполнялось равенство (2). Данный способ синхронизации, в отличие от «стандартного» релятивистского, является транзитивным. При его использовании наблюдатели не столкнутся с описанным ранее противоречием при синхронизации часов по кругу. Все часы будут синхронны, как с точки зрения неподвижного наблюдателя, так и с точки зрения наблюдателя на диске.
Мы получили, что синхронизировать часы на ободе вращающегося диска можно, пользуясь только соображениями симметрии, без каких бы то ни было условий или допущений. Мы получили также, что безусловно симметричные способы синхронизации часов на ободе вращающегося диска приводят к тому, что события, одновременные для наблюдателя на диске, – будут одновременными и для неподвижного наблюдателя.
Почему же «стандартный» релятивистский способ синхронизации в данном случае дает другой результат? Ответ очевиден – потому что при использовании этого способа условия распространения сигнала «туда» и «обратно» отличаются; «туда» сигнал идет по ходу вращения диска, а «обратно» – против его вращения. Для наблюдателя на диске условия движения вдоль обода в противоположных направлениях различны. А ведь согласно требованиям самой же теории относительности [2 с.148]: «Этот способ должен быть таким, чтобы мы были абсолютно уверены, что явления передачи сигналов из A в B нисколько не отличаются от явлений передачи сигналов из B в A». Следовательно, «стандартный» релятивистский способ в данном случае непригоден, а утверждение теории относительности о невозможности непротиворечивой синхронизации часов на ободе вращающегося диска необоснованно.
Заключение.
Часто говорят, что критика теории относительности – это шаг назад, ведь она решила проблему неинвариантности уравнений Максвелла относительно преобразований Галилея. Вот, например, цитата из книги Р. Фейнмана [9 с.7]:
«Однако уравнения Максвелла, по-видимому, не подчиняются принципу относительности: если преобразовать их подстановкой (15.2), то их вид не останется прежним».
Подстановка (15.2) это преобразования координат Галилея. Обратите внимание, Фейнман не утверждает, он говорит «по-видимому», и не зря. Инвариантность своих уравнений относительно преобразований Галилея анализировал уже сам Максвелл в «Трактате об электричестве и магнетизме». Этот параграф так и называется «Об изменении уравнений электродвижущей интенсивности в случае, когда оси, к которым они относятся, движутся в пространстве» [14 с. 467]. Вывод, который делает Максвелл, говорит сам за себя [14 с. 469]: «Отсюда вытекает, что электродвижущая интенсивность выражается формулой того же самого типа, будут ли движения проводников отнесены к неподвижным осям или к осям, движущимся в пространстве».
Уравнения Максвелла не являются полной системой уравнений электродинамики. Для полноты им не хватает материальных уравнений. Причем известно, что сами уравнения Максвелла инвариантны относительно преобразований Галилея, это легко проверить непосредственной подстановкой, вопросы возникают только с материальными уравнениями. Вот более-менее современное описание этой проблемы, представленное группой ученых в журнале УФН [15 с.525], цитата:
«Довольно распространено мнение, что преобразования Лоренца
x′ = γ (x – Vt), y′ = y, z′ = z, t′ = γ (t – Vc–2x), (1.1)
где γ = [1 – (V2/c2)]–1/2 выделены среди других преобразований координат и времени (например, классических преобразований Галилея) тем, что, в отличие от последних, они (и только они) оставляют инвариантными уравнения Максвелла. Хорошо известно, однако, что уравнения Максвелла
могут быть записаны в 4-тензорной форме без конкретизации связи между векторами полей в веществе. А это означает не только их лоренц-инвариантность (что обычно подчеркивается в физической литературе), но также инвариантность относительно произвольных невырожденных линейных преобразований пространственно-временных переменных (аффинная ковариантность).
Иначе говоря, если вместе с координатами по соответствующему закону пересчитывать поля и источники (как это делается, в частности, и в специальной теории относительности (СТО)), уравнения (1.2) сохранят свой вид при любых линейных преобразованиях, включая и галилеевские. Разумеется, каждому такому преобразованию (т.е. каждой системе 4-координат) будут при этом соответствовать свои материальные уравнения среды.
С формальной точки зрения преобразования Лоренца выделены только тем, что в вакууме они сохраняют вид материальных уравнений среды (D = E, B = H), что физически и соответствует релятивистскому постулату инвариантности скорости света. Для полей в веществе преобразования Лоренца таким преимуществом уже не обладают …». Конец цитаты.
Учитывая, что вакуум в общем случае тоже является средой распространения электромагнитных полей, то почему бы не допустить возможность изменения материальных уравнений и для вакуума?
Библиографический список
- Рейхенбах Г. Философия пространства и времени, перевод с английского Ю.Б. Мочанова, общая редакция А.А. Логунова. – М.: Прогресс, 1985 (Philosophy of Space and Time by Hans Reichenbach. Translated by Maria Reichenbach and John Freund: witch introductory remarks by Rudolf Carnap. New York 1958)
- Эйнштейн А. Собрание научных трудов. В 4 т. Т.I. Работы по теории относительности 1905-1920; под редакцией И.Е. Тамма, Я.А. Смородинского, Б.Г. Кузнецова. – М.: НАУКА, 1965
- Борн М. Эйнштейновская теория относительности, перевод с английского Н.В. Мицкевича. – 2-е изд., испр. – М.: МИР, 1972 (EINSTEIN’S THEORY OF RELATIVITY by Max Born. Revised edition prepared with the collaboration of Gunter Leibfried and Walter Biem. Dover Publications Inc. New York 1962)
- Ландау Л.Д., Лившиц Е.М. Теоретическая физика: Учеб. пособие. В 10 т. Т.II. Теория поля. – 7-е изд., испр. – М.: НАУКА, 1988. – 512 с. – ISBN 5-02-014420-7
- Тяпкин А.А. Выражение общих свойств физических процессов в пространственно-временной метрике специальной теории относительности // УФН. 1972. Т. 106, вып. 4. С. 617-659 (http://ufn.ru/ru/articles/1972/4/c/)
- Мёллер К. Теория относительности. – 2-е изд. – Пер. с англ. Под ред. проф. Д. Иваненко. – М.: Атомиздат, 1975 (THE THEORY OF RELATIVITY by C. Möller, second edition, Clarendon press, Oxford, 1972)
- Тоннела Мари-Антуанетт, Основы электромагнетизма и теории относительности, перевод с французского Г.А. Зайцева. – М: Издательство иностранной литературы, 1962 (Marie-Antoinette TONNELAT, Professeur a la Faculte des Sciences de Paris, LES PRINCIPES DE LA THEORIE ELECTROMAGNETIQUE ET DE LA RELATIVITE; MASSON ET CIE, EDITEURS; PARIS, 1959)
- Грюнбаум А. Философские проблемы пространства и времени, перевод с английского Ю.Б. Молчанова, общая редакция Э.М. Чудинова. – М.: Прогресс, 1969 (Philosophical problems of space and time, Adolf Grünbaum; Andrew Mellon Professor of Philosophy UNIVERSITY OF PITTSBURGH; New York Alfred A. Knopf, 1963)
- Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. В 9 т. Т.II. Пространство, время, движение. – М.: МИР, 1965
- Угаров В.А. Специальная теория относительности. – 2-е изд., испр. – М.: НАУКА, 1977
- Фок В.А. Теория пространства, времени и тяготения. – 2-е изд., дополненное. – М.: Государственное издательство физико-математической литературы, 1961
- Жуков А.И. Введение в теорию относительности. – М.: Государственное издательство физико-математической литературы, 1961
- Мардер Л. Парадокс часов. – Пер. с анг. А.А. Бейлинсона. – М.: МИР, 1974 (L. Marder, TIME AND THE SPACE-TRAVELLER, LONDON∙GEORGE ALLEND AND UNWIN LTD RUSKIN HOUSE MUSEUM STREET, 1971)
- Максвелл Д.К. Избранные сочинения по теории электромагнитного поля, перевод З.А. Цейтлина под ред. П.С. Кудрявцева. – М.: Государственное издательство технико-теоретической литературы, 1952. – 687 с.
- Миллер М.А., Сорокин Ю.М., Степанов Н.С. Ковариантность уравнений Максвелла и сопоставление электродинамических систем // УФН. 1977. Т. 121, вып. 3. С. 525-538 (http://ufn.ru/ru/articles/1977/3/e/)