В работе рассматривается движение космического аппарата (КА) с инерционными исполнительными органами (ИИО) на высокоэллиптической орбите (ВЭО). При насыщении системы ИИО КА применяют различные способы разгрузки накопленного кинетического момента. Обычно управление центром масс КА и разгрузка ИИО автоматических КА производится с использованием ракетных двигателей малой тяги, в том числе электроракетных [1]. Естественно, наиболее предпочтительными способами управления кинетическим моментом являются способы, без расхода рабочего тела. Для этой цели в работе используется гравитационный момент.
1.Уравнения движения. Линеаризованные уравнения углового движения КА в общем виде при наличии ИИО в не разделяющихся каналах крена и рыскания для ВЭО при учете действия гравитационного момента в случае применения теоремы об изменении кинетического момента [2, с. 147] в соответствии с [3] имеют вид:
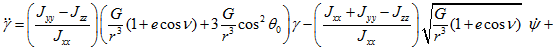
.gif)
.gif)
.gif) (1)
(1)
![]()
![]() .
.
Здесь ![]() главные центральные моменты инерции КА,
главные центральные моменты инерции КА, ![]() кинетические моменты ИИО в каналах крена и рыскания соответственно,
кинетические моменты ИИО в каналах крена и рыскания соответственно, ![]() моменты реакций в подшипниках ИИО, через который осуществляется как управляющее воздействие на корпус КА с целью поддержания его ориентации, так и одновременное регулирование (в частном случае, разгрузка) накопленного кинетического момента ИИО в каналах крена и рыскания соответственно,
моменты реакций в подшипниках ИИО, через который осуществляется как управляющее воздействие на корпус КА с целью поддержания его ориентации, так и одновременное регулирование (в частном случае, разгрузка) накопленного кинетического момента ИИО в каналах крена и рыскания соответственно, ![]() –малый угол отклонения от углового положения (0, 0, 0) в канале тангажа;
–малый угол отклонения от углового положения (0, 0, 0) в канале тангажа; ![]() ,
,![]() гравитационный параметр,
гравитационный параметр, ![]() радиус-вектор, направленный из центра Земли в центр масс КА;
радиус-вектор, направленный из центра Земли в центр масс КА; ![]() эксцентриситет орбиты,
эксцентриситет орбиты, ![]() -истинная аномалия.
-истинная аномалия.
При переходе к описанию в пространстве состояний уравнения (1) имеют следующий вид:
где .gif) ;
; 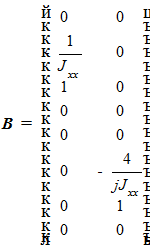 ;
; .gif) - вектор состояния;
- вектор состояния;
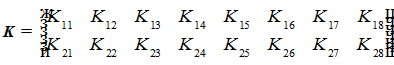 - коэффициенты обратной связи;
- коэффициенты обратной связи; ![]() - углы крена и рыскания соответственно;
- углы крена и рыскания соответственно;
.gif) ,
, .gif) ,
, 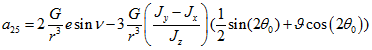 ;
; .gif)
![]() ;
; 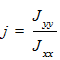 .
.
2. Постановка задачи в пространстве состоянии.
Для заданной линейной MIMO–система (Multi Input Multi Output)
![]()
где ![]() – вектор состояния,
– вектор состояния, ![]() – вектор выхода,
– вектор выхода,
а ![]() ,
, ![]() ;
;
![]()
требуется определить закон обратной связи
![]()
обеспечивающий:
![]() ,
,
![]()
Здесь под ![]() понимается левая полуплоскость комплексной плоскости.
понимается левая полуплоскость комплексной плоскости.
3. Описание алгоритма управления ориентацией КА на участке орбиты свободном от выполнения целевых задач в не разделяющихся каналах крена и рыскания.
В работе [4] для не разделяющихся каналов крена и рыскания на основе метода точного размещения полюсов, суть которого изложена в [5], были представлены законы управления ориентацией при одновременном регулировании кинетического момента ИИО КА на ВЭО для следующих соотношений моментов инерции КА:
В данной работе автором получены коэффициенты обратной связи по состоянию для произвольных значений моментов инерции. Итак, вычисляя декомпозицию системы аналогично тому, как представлено в [4], последовательно выполнив вычисления коэффициентов обратной связи, получаем:
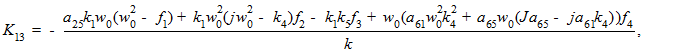
.gif)
.gif)
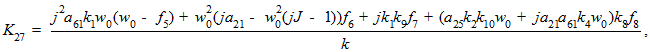
Для простоты представления коэффициентов были введены следующие обозначения:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
![]()
![]() .
.
В качестве ![]() , которые в соответствии с методом точного размещения полюсов являются корнями характеристического уравнения
, которые в соответствии с методом точного размещения полюсов являются корнями характеристического уравнения ![]() , где
, где ![]() – размерность рассматриваемой системы, принимались корни полинома Баттерворта восьмого порядка, таким образом, что:
– размерность рассматриваемой системы, принимались корни полинома Баттерворта восьмого порядка, таким образом, что:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Здесь ![]() ,
, ![]() – радиус окружности, на которой расположены
– радиус окружности, на которой расположены ![]() .
.
4. Заключение.
Получены законы управления ориентацией при одновременном регулировании накапливаемого кинетического момента ИИО КА на рассматриваемом участке ВЭО с использованием метода точного размещения полюсов в не разделяющихся каналах крена и рыскания для произвольных соотношения моментов инерции. Эти законы обеспечивают асимптотическую устойчивость, определенный запас устойчивости и имеют явную зависимость коэффициентов усиления законов управления от параметров орбиты, массово-инерционных характеристик КА.
Библиографический список
- Платонов В.Н. Одновременное управление движением центра масс и вокруг центра масс при маневрах космических аппаратов на геостационарной и высокоэллиптических орбитах с использованием электроракетных двигателей // Космическая техника и технологии. 2013. № 1, С.56–66.
- Раушенбах Б.В., Токарь Е.Н. Управление ориентацией космических аппаратов. М.: Наука, 1974.
- Тимаков Н.С. Исследование управляемого углового движения космического аппарата на высокоэллиптической орбите // Навигация и управление движением. Матер. IX конф. молодых ученых. СПб, 2007. С. 330–336.
- Воробьева Е.А., Зубов Н.Е., Микрин Е.А. Безрасходная разгрузка накопленного кинетического момента инерционных исполнительных органов автономного космического аппарата на высокоэллиптической орбите// Инженерный журнал: наука и инновации, 2013. №10.(22), С. 1– 18.
- Зубов Н.Е., Микрин Е.А., Мисриханов М.Ш., Рябченко В.Н. Синтез развязывающих законов стабилизации орбитальной ориентации космического аппарата // Изв. РАН. ТиСУ. 2012. № 1. С. 92–108.
