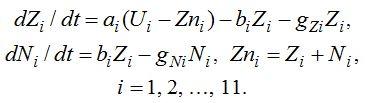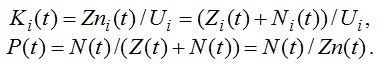Важное направление развития современной теории обучения состоит в изучении дидактических систем методом математического [2] и имитационного (или компьютерного) моделирования [4, 8]. Используя метод имитационного моделирования, ученые могут исследовать сложные объекты и процессы в случаях, когда проводить реальные эксперименты с ними невозможно или нецелесообразно. Сущность этого метода состоит в построении компьютерной модели реальной системы и проведении серии вычислительных экспериментов с целью понимания поведения системы или оценки различных стратегий управления, обеспечивающие ее функционирование. Высокое быстродействие современных ЭВМ позволяет обрабатывать большие объемы информации и достаточно быстро осуществлять компьютерную имитацию. Изменяя начальные данные и параметры модели, можно исследовать пути развития системы, определить ее состояние в конце обучения. В этом состоит преимущество данного подхода по сравнению с методом качественного анализа. Поэтому проблема исследования различных математических и компьютерных моделей процесса обучения имеет большое значение для развития дидактики.
При имитационном моделировании процесса обучения часто считают, что все элементы учебного материала усваиваются одинаково прочно [2 – 6]. Но это не так: психологи установили, что те знания, которые включены в учебную деятельность ученика, запоминаются значительно прочнее, чем знания, которые школьник не использует. Чтобы компьютерная модель более точно соответствовала реальному процессу обучения, нужно учесть, что: 1) прочность усвоения различных элементов учебного материала неодинакова, поэтому их следует разделить на несколько категорий; 2) прочные знания забываются существенно медленнее непрочных; 3) непрочные знания при их использовании учащимся постепенно трансформируются в прочные знания, превращаются в навыки [8, с. 69 – 72]. Ученика можно охарактеризовать коэффициентами обучения a_i, коэффициентами перехода непрочных знаний в прочные b_i и коэффициентами забывания g_zi и g_ni (i = 1, 2, …, 11). Предлагаемая двухкомпонентная модель обучения выражается системой уравнений [7 – 9]:
Здесь U_i –– уровень требований, предъявляемый учителем в i–том классе, который равен сообщаемым знаниям Z_0i, Zn_i –– суммарные знания ученика за i–тый класс, Z_i –– количество непрочных знаний за i–тый класс, имеющих высокий коэффициент забывания g_zi, а N_i –– количество у ученика прочных знаний за i–тый класс, которые имеют низкий коэффициент забывания g_ni. Состояние ученика в любой момент времени t может быть задано матрицами Z_i = (Z_1, Z_2, …, Z_11) и N_i = (N_1, N_2, …, N_11), которые характеризуют количества усвоенных прочных и непрочных знаний за 1, 2, …, 11 классы. При обучении в i–том классе увеличиваются количества знаний Z_i и навыков N_i (i = 1, 2, … 11), а также количества знаний за предыдущие классы, к которые используются учеником при изучении текущей темы. Коэффициент усвоения учеником учебного материала за i–ый класс и коэффициент прочности знаний ученика (то есть доля прочных знаний от общего их количества) в данный момент времени t:
Рассматриваемая модель обучения должна учитывать: 1) основные закономерности обучения и забывания [1]; 2) превращение непрочных знаний в прочные знания (или навыки), которые имеют меньший коэффициент забывания; 3) увеличение количества изучаемой информации и ее сложности (степени абстрактности) при переходе ученика в старшие классы; 4) повышение коэффициента усвоения школьника при переходе в следующий класс; 5) использование учеником j–того класса учебного материала, изученного в предыдущих 1, 2, …, (j–1)–ом классах; 6) применение знаний из учебника j–того класса в повседневной жизни во время каникул и после окончания школы.
Для моделирования изменения знаний во время обучения в школе и после ее окончания следует задать параметры ученика, его начальное состояние при t = 0 и распределение сообщаемой учебной информации [7–9]. Ученик характеризуется:
1. Коэффициентами усвоения a_i, которые определяют быстроту перехода знаний учителя Z_0i = U_i за i–тый класс в непрочные знания ученика Z_i. Значения a_i по мере обучения монотонно возрастают, так как чем больше информации ученик усвоил, тем легче он запоминает новую информацию. Коэффициенты a_i можно задать так: A_i = (1, 1.2, 1.4, 1.6, 1.9, 2.2, 2.5, 2.8, 3.1, 3.4, 3.7), a_i =A_i / 12.
2. Коэффициентами формирования навыков b_i = a_i /80 (i = 1, 2, … 11), характеризующими скорость превращения непрочных знаний в прочные; при этом Z_i уменьшается, а N_i растет на ту же величину.
3. Коэффициентами забывания непрочных g_zi и прочных g_ni знаний, изученных в i–том классе. Известно, что знания, полученные в 1 – 4 классах, используются человеком в повседневной жизни и поэтому запоминаются хорошо. В старших классах увеличивается степень абстрактности учебной информации, то есть приобретаемые знания сильнее оторваны от повседневной жизни и имеют более высокий коэффициент забывания. Эти коэффициенты можно задать так: g_i = (10, 10, 10, 11, 12, 13, 14, 15, 16, 17, 18), g_zi = g_i / 200, g_ni = g_zi/60. Так как забывание происходит по экспоненциальному закону, то время забывания половины имеющихся знаний равно T = ln2 / g. Например, для шестого класса g_z6 = 0,065 (1/месяц) и g_n6 = 0,00108 (1/месяц). Это означает, что для непрочных знаний, изученных в шестом классе T_z = 10,7 месяца, а для прочных T_n = 53 года.
Внешнее воздействие, оказываемое на ученика задается:
1. Распределением учебной информации в течение всего времени обучения в школе; оно задается массивом U_i = (10, 12, 14, 17, 20, 24, 29, 35, 42, 50, 59), где U_i –– уровень требований учителя в –том классе, который равен количеству сообщенных им знаний.
2. Коэффициентами обращения ученика j–того класса к знаниям, полученным в i–том классе, задаваемыми двумерной треугольной матрицей:
Из e[3, 11] = 0,7 следует, что, обучаясь в одиннадцатом классе, ученик использует 70 процентов знаний, полученных в третьем классе.
3. Коэффициентом использования информации, изученной в i–том классе, во время каникул и после обучения, который можно задать так: c_i = 0,3 при i < 5 и c_i =0,3/(i – 4) при i > 4. В обозначенные промежутки времени человек читает книги, выполняет математические действия, смотрит фильмы, разговаривает на иностранном языке, использует различные устройства и программные продукты. При этом в большей степени увеличиваются и закрепляются знания, полученные в 1 – 4 классах, и в меньшей степени –– знания из 9 – 11 классов, уровень абстрактности которых выше.
Значения U_i, e[i, j] и c_i должны отражать особенности школьной программы. Параметры a_i, b_i, g_zi и g_ni характеризуют гипотетического ученика, который успешно учится в школе. Используется программа 1; в ней время измеряется в месяцах. Считается, что из 12 месяцев в году 3 месяца ученик отдыхает, а 9 – учится. За начало отсчета t = 0 принят первый день обучения в первом классе, начальный уровень знаний ученика: Zn(0)=0.
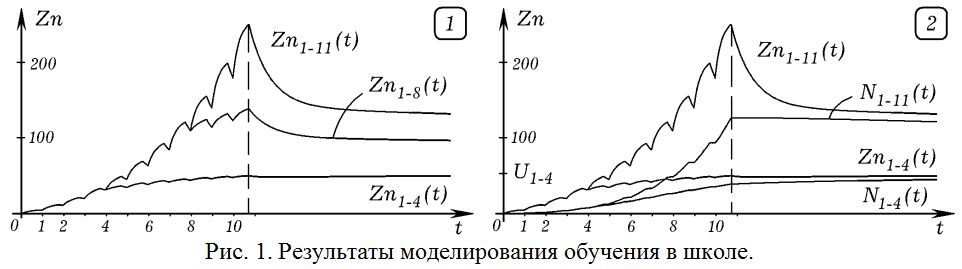
На рис. 1 и 2 представлены результаты имитационного моделирования изменения количества знаний гипотетического школьника в течение 11 лет посещения школы и 10 лет после окончания обучения. Понятно, что на практике реализуются самые разнообразные ситуации, отличающиеся как учебной программой, так и параметрами конкретных школьников.
На рис. 1.1 приведены графики зависимостей количества знаний ученика за 1 – 4, 1 – 8 и 1 – 11 классы от времени. Из рис. 1.2 видно, что в процессе обучения (1 – 11 годы) суммарное количество знаний Zn(t) в среднем возрастает, а после обучения –– снижается в первую очередь из–за забывания непрочно усвоенных знаний. Провалы в графике Zn(t) соответствуют летним каникулам, в течение которых школьник забывает часть непрочных знаний. Количество прочно усвоенных знаний (или навыков) N(t) в течение обучения повышается, а после обучения практически не изменяется. Графики Zn{1–4}(t) и N{1–4}(t) показывают динамику изменения количества суммарных знаний и навыков (прочных знаний), соответствующих 1 – 4 классам в течение всего рассматриваемого промежутка t от 0 до 20 лет. Речь идет о навыках чтения, письма, выполнения арифметических операций, элементарных знаний об окружающем мире, которые человек усваивает в начальной школе и затем использует всю свою жизнь. Видно, что их количество монотонно возрастает, стремясь к предельному значению U{1–4} = U_1 + U_2 + U_3 + U_4, равному информации, которое должен в идеале усвоить ученик в 1 – 4 классах.
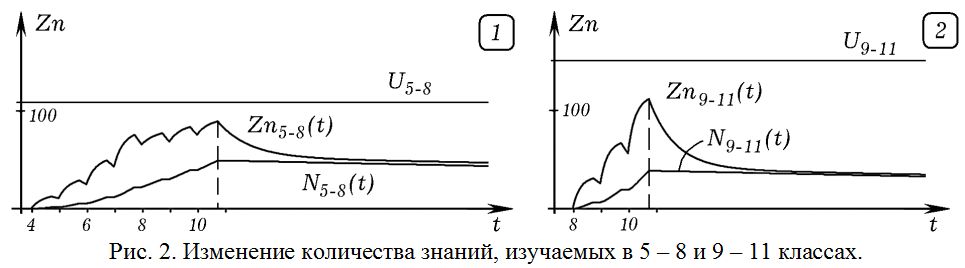
На рис. 2.1 показаны графики изменения количества знаний Zn{5–8}(t) и N{5–8}(t), изучаемых в 5 – 8 классах. Учебный материал имеет более высокий уровень абстрактности и в меньшей степени используется в повседневной жизни, поэтому суммарное количество знаний Zn{5–8} к концу школы (t = 11 лет) примерно равно 0,8*U{5–8}, количество прочных знаний N{5–8} примерно равно 0,5*U{5–8}, от общего уровня требований учителя U{5–8} =U_5+U_6+U_7+U_8. Так как приобретенные в 5 – 8 классах знания также частично используются в повседневной жизни, то после окончания обучения их суммарное количество сначала снижается, а затем остается постоянным на уровне 0,5*U{5–8}.
На рис. 2.2 представлены графики Zn{9–11}(t) и N{9–11}(t), показывающие изменение суммарного количества знаний и количества прочных знаний, изучаемых в 9 – 11 классах. Из них следует, что к концу обучения (t = 11 лет) суммарное количество знаний Zn{9–11} достигает своего максимума 0,7*U{9–11}, в то время как N{9–11} примерно равно 0,25*U{9–11}. При этом U{9–11} – суммарное количество учебной информации, содержащееся в учебниках 9 – 11 классов, которое в идеале должен усвоить учащийся. При подборе коэффициентов считалось, что гипотетический ученик после успешного обучения в школе помнит более 0,6*U{9–11}, а за летние каникулы после 10 класса забывает около трети усвоенного в 10 классе материала (рис. 2.2). Улучшение модели требует уточнения входящих в нее коэффициентов.
Предлагаемая имитационная модель обучения в школе учитывает, что: 1) изменение количества знаний человека происходит в соответствии с известными законами научения и забывания; 2) во время обучения на фоне увеличения общего количества знаний ученика, происходит переход непрочных знаний в прочные знания, которые забываются медленнее; 3) с ростом номера класса количество изучаемой информации и ее сложность (степень абстрактности) увеличиваются, коэффициент забывания растет; 4) по мере обучения в школе происходит повышение коэффициента усвоения ученика; 5) во время обучения в j–том классе ученик использует материал, изученный в 1, 2, …, (j–1)–том классах; 6) во время каникул и после окончания школы человек использует изученный материал в повседневной жизни, часть непрочных знаний становится прочными.
Библиографический список
- Атанов Г.А., Пустынникова И.Н. Обучение и искусственный интеллект, или Основы современной дидактики высшей школы. Донецк: Изд–во ДОУ, 2002. 504 с.
- Добрынина Н.Ф. Математические модели распространения знаний и управления процессом обучения студентов. Фундаментальные исследования. 2009. N 7. С. 7 – 9.
- Доррер А.Г., Иванилова Т.Н. Моделирование интерактивного адаптивного обучающего курса // Современные проблемы науки и образования. 2007. N 5.
- Ивашкин Ю.А., Назойкин Е.А. Мультиагентное имитационное моделирование процесса накопления знаний // Программные продукты и системы. 2011. N 1. С. 47 – 52.
- Кудрявцев В.Б., Вашик К., Строгалов А.С., Алисейчик П.А., Перетрухин В.В. Об автоматном моделировании процесса обучения. Дискретная математика. 1996. Т. 8., вып. 4. С. 3 – 10.
- Лаптев В.В., Сербин В.И. Изучение поведения моделей обучения с использованием марковского процесса // Вестник АГТУ. Управление, вычислительная техника и информатика. 2010. N 1. С 42 – 45.
- Майер Р.В. Двухкомпонентная модель изучения курса: результаты имитационного моделирования // Психология, социология и педагогика. 2014. № 11 [Электронный ресурс]. URL: http://psychology.snauka.ru/2014/11/3835.
- Майер Р.В. Кибернетическая педагогика: Имитационное моделирование процесса обучения: монография. Глазов: Глазов. гос. пед. ин–т, 2014. 141 с. URL: http://maier-rv.glazov.net
- Майер Р.В. Многокомпонентная модель обучения и ее использование для исследования дидактических систем // Фундаментальные исследования: Педагогические науки. 2013. N 10. С. 2524 – 2528.