Моделирование социально-экономических процессов по своей сути является воспроизведением данных процессов в малых экспериментальных формах, в искусственно созданных условиях. Чаще всего для этих целей используется математическое моделирование, описывающее социально-экономические процессы при помощи математических зависимостей. 
Созданная математическая модель обычно подкрепляется реальными статистическими данными, а результаты расчетов, выполненные в рамках построенной модели, позволяют строить прогнозы и проводить объективные оценки. 
По фактору времени принято выделять статические и динамические модели. Статические модели описывают поведение объекта в какой-либо конкретный момент времени. Данные модели применяют для описания статических систем, путем характеристики их состояния в заданный момент времени. При этом полученные, при помощи статического моделирования данные, не дают достоверного представления о динамической системе, можно судить лишь о ее поведении в строго определенный момент времени. 
Динамические модели – модели, учитывающие взаимосвязи переменных во времени. Такие модели не сводятся к простой сумме ряда статических моделей, а описывают силы и взаимодействия, определяющие ход процессов в экономических системах. Модель является динамической, если в данный момент времени она учитывает значения входящих в нее переменных, относящихся как к текущему, так и к предыдущим моментам времени. 
В экономических исследованиях очень часто для изучения факторов, определяющих уровень и динамику экономических процессов, используются модели корреляционно-регрессионного типа. При этом задачи корреляционного анализа сводятся к измерению тесноты известной связи между изменяющимися признаками, определению неизвестных причинных связей и оценке факторов, оказывающих наибольшее влияние на результативный признак. Задачи регрессионного анализа заключаются в выборе типа модели, установлении степени влияния независимых переменных на зависимую переменную и определении расчетных значений зависимой переменной. 
Модели корреляционно-регрессионного типа в зависимости от количества факторов, включенных в уравнение регрессии, бывают простого (парного) и множественного вида. В свою очередь, парная регрессия и корреляция может определяться как наличием линейных связей между переменными, так и наличием нелинейных связей. 
Простая регрессия представляет собой модель, где среднее значение зависимой (объясняемой) переменной yрассматривается как функция одной независимой (объясняющей) переменной x, то есть данная модель имеет вид:
. (1)
Парная регрессия достаточна, если имеется доминирующий фактор, который и используется в качестве объясняющей переменной. В уравнении регрессии корреляционная по сути связь признаков представляется в виде функциональной связи, выраженной соответствующей математической функцией. Практически в каждом отдельном случае величина y, складывается из двух слагаемых:
, (2)
где  – фактическое значение результативного признака;  – теоретическое значение результативного признака, найденное по соответствующему уравнению регрессии;  – случайная величина, характеризующая отклонения реального значения результативного признака от теоретического, найденного по уравнению регрессии.
Случайная величина  включает влияние неучтенных в модели факторов, случайных ошибок и особенностей измерения. Ее присутствие в модели обусловлено тремя источниками: спецификацией модели, выборочным характером исходных данных и особенностями измерения переменных. 
При построении регрессионных моделей могут использоваться как линейные, так и нелинейные функции. 
Множественная регрессия – уравнение связи с несколькими объясняющими (независимыми) переменными:
. (3)
Множественная регрессия широко используется при решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах и целого ряда других вопросов эконометрики. Основная цель множественной регрессии – построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а так же совокупное воздействие их на моделируемый показатель. 
Основной недостаток использования регрессионных моделей в экономике – не всегда достоверные результаты прогнозов, рассчитанных по данным моделям. Несмотря на то, что данные модели при проверке и обладают высоким качеством, но они не учитывают влияние, оказываемое предыдущими результатами на результат текущий. Это может в определенных случаях искажать прогнозные значения, полученные при помощи данных моделей. 
Для большей достоверности полученных прогнозов в экономической и управленческой деятельности стоит учитывать динамические особенности прогнозируемых явлений.
Одним из типов динамических моделей, применяемых для исследования социально-экономических процессов, являются модели с распределенным лагом, в которых значения переменных за прошлые периоды непосредственно включены в модель. 
В общем виде рассмотрим алгоритм построения модели социально-экономических процессов при помощи построения динамической модели с распределенным лагом – моделью с лагами Алмон: 
, (4)
где  - максимальная величина лага; , , , , – параметры оценок; 
 – текущий момент времени;  - случайная величина, характеризующая отклонения реального значения результативного признака от теоретического. 
Данный метод хорошо описан в труде Елисеевой И.И. [1] и реализован на примере моделирования зависимости ВВП от инвестиций в экономику США. Исходная статистическая информация представлена в табл. 1.

Пусть максимальная длина лага равна четырем, тогда вид лаговой модели будет следующим:

 (5)

Для определения коэффициентов модели воспользуемся обычным МНК, с помощью стандартной функции ExcelЛинейн. Результаты моделирования представлены на рисунке 1.

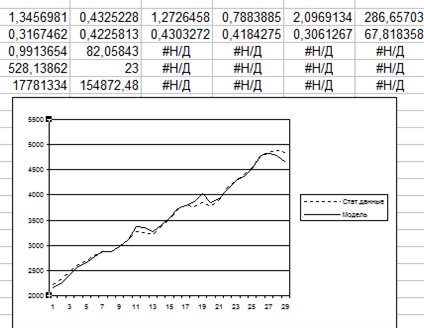
Рисунок 1 – результаты моделирования

Конкретный вид модели:

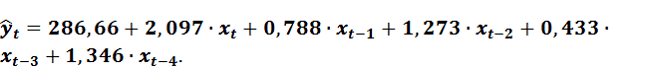 (6)

Из рисунка видно, что совпадение экспериментальных данных и результатов моделирования достаточно неплохое. Подтверждением тому является высокий коэффициент детерминации = 0,9914. Однако коэффициенты при лаговых переменных  и  являются статистически незначимыми. Кроме того применение метода МНК к таким моделям в общем случае некорректно по ряду причин:Высокий уровень мультиколлинеарности факторов модели;
При большой величине лага снижается число наблюдений, используемых при моделировании, что естественным образом ведет к снижению числа степеней свободы;
Неизбежным также является наличие автокорреляции остатков.Вышеперечисленные факторы свидетельствуют о значительных нарушениях предпосылок МНК, что приводит к неэффективным, а зачастую и к смещенным оценкам. 
Следует отметить, что несостоятельность модели становится более выраженной при увеличении количества коэффициентов, когда по смыслу задачи ожидается влияние с большим запаздыванием.
Для преодоления этих трудностей обычно предлагается та или иная форма «гладкости» распределения лагов. Это приводит к уменьшению числа оцениваемых параметров. 
Пусть модель с распределенным лагом порядка  имеет вид:

 (7)

В преобразовании Алмон коэффициенты модели представлены степенными полиномами, факторами которых является величина лага. Для полинома k – ой степени эта зависимость имеет вид:
 (8)
Если подставить значения (8) в исходную модель (7), то получим модель вида:

 (9)

где  
Для нашего примера, с максимальным лагом =4, модель преобразуется к виду:

 (10)

где 


Оценим (10) с помощью МНК. Результаты моделирования представлены на рисунке 2.

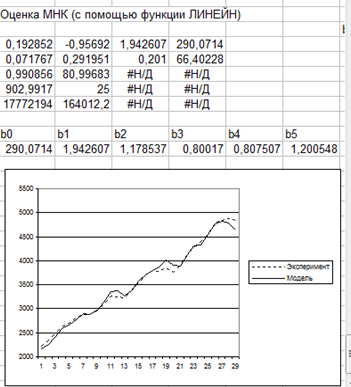
Коэффициенты модели Алмон:
, , , .
Подставив эти значения в (4) получим модель с распределенным лагом

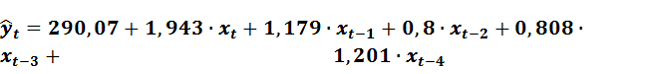 (11)

В этом случае коэффициент детерминации даже несколько ниже, чем в предыдущем случае R² = 0,99, однако все коэффициенты являются статистически значимыми. 
Данный метод имеет два неоспоримых преимущества. Во-первых, он достаточно универсален и может быть применен для моделирования процессов, которые характеризуются разнообразными структурами лагов. Во-вторых, при относительно небольшом количестве переменных, которое не приводит к потере значительного числа степеней свободы, с помощью метода Алмон можно построить модели с распределенным лагом любой длины. 
Результаты исследований с использованием этих преобразований показали, что, несмотря, на некоторое снижение коэффициента детерминации, эффективность оценок повышается, они становятся статистически более значимыми. Однако не снимается главная проблема – наличие мультиколлинеарности. Кроме того величина лага должна быть известна заранее. 
Выбор длины лага меньше реального приведет к искажению динамики процесса: не будут учтены факторы, оказывающие значительное влияние на результат. В этом случае остатки будут неслучайными и оценки по МНК окажутся неэффективными и смещенными. Проявление этих проблем будет заметным особенно при определении прогнозных значений зависимой переменной с использованием других статистических данных.
Выбор большей величины лага по сравнению с ее реальным значением приведет к включению в модель слабо значимых факторов, а, следовательно, к снижению эффективности оценок. Кроме того при этом происходит уменьшение объема выборки, используемой для моделирования, что ведет также к снижению эффективности и состоятельности оценок.
Для моделирования динамики можно использовать непрерывную модель, представленную дифференциальным уравнением. Наиболее предпочтительным является использование линейных уравнений первого и второго порядков:

 (12)
 (13)

где  – постоянная времени; ζ- коэффициент затухания; – установившееся значение.
В (12) и (13) под установившимся значением понимается тренд между переменными  и  в установившемся режиме, когда u = const и отклики на «предысторию» значений объясняющей переменной завершены.
Трендовая составляющая моделей (12) и (13) может быть как линейной, так и нелинейной, например:

 (14)
 (15)

Для оценки параметров модели Т, ζ,   , можно использовать дискретно-непрерывный метод идентификации, основанный на соотношениях дискретного линейного фильтра Калмана [2], [3]. 
Используя статистику (табл. 1), построим математическую модель зависимости ВВП от инвестиций в форме (12), (14)
 (16)
где параметры модели Т, ,  подлежат оцениванию. 
Для идентификации параметров Т, ,  составим расширенную модель вида:

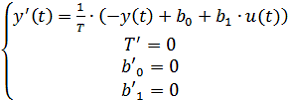. (17)

Обозначим . Тогда исходную систему для идентификации можно представить в виде:

 (18)

где ,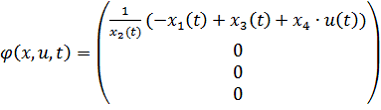
 вектор шумов с дисперсионной матрицей 
.
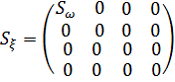Модель измерения координат состояния имеет вид:

 (19)

где  
Модель измерения управления

 (20)

где  - измеренные значения,  - истинные значения управления.
В (19) и в (20)  ,  - центрированные случайные шумы с известными дисперсиями: .
Для оценки вектора  модели (18) воспользуемся алгоритмом дискретно-непрерывного метода.
Оценка параметров модели и численное моделирование динамики инвестиций были реализованы с помощью ППП Mathcad.
Результаты идентификации представлены на рисунке 3.

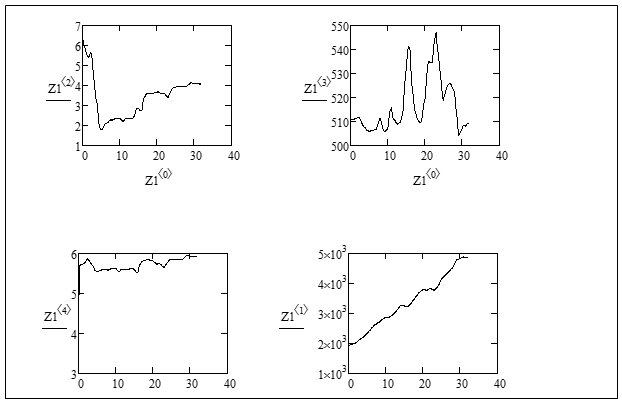
Рисунок 3- Результаты идентификации. Z1⁽¹⁾ - , Z1⁽²⁾ - , Z1⁽³⁾ - ,

Z1⁽⁴⁾Исследования показали, что эффективность оценки коэффициента  достаточно низкая, так как в эксперименте нет установившегося значения x(t). Поэтому пришлось варьировать начальное значение этого коэффициента: если тенденция его оценки была возрастающая и не была установившейся, то начальное значение еще увеличивали, до тех пор, пока тенденция не сменила знак, т.е. стала убывающей. Затем начальное значение принималось в районе смены тенденции, «зажималась» его начальная дисперсия (дисперсия принималась небольшой, чтобы этот коэффициент не «раскачивался») и осуществлялось окончательное оценивание, результаты которого представлены на рисунке. Итоговые оценки были выбраны следующими: =509; =5,9; Т = 3,92.
Результаты проверки соответствия модели экспериментальным данным представлены на рисунок 4.

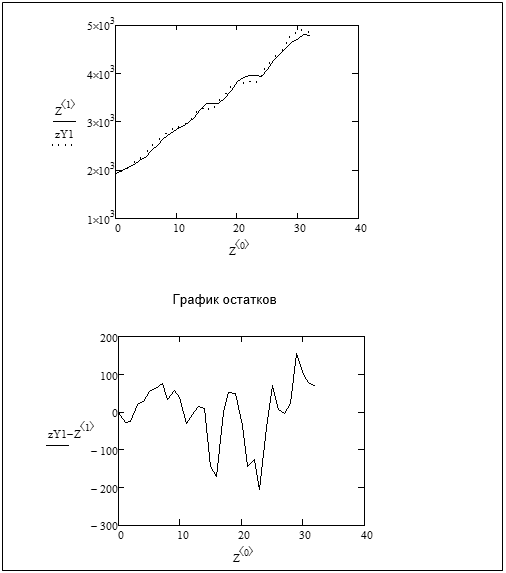
Из рисунка видно, что совпадение модельных и экспериментальных данных достаточно высокое. Свидетельством тому является значение коэффициента детерминации R² = 0,992.
Следующим этапом проверки адекватности модели экспериментальным данным была проверка полноты моделирования динамических свойств модели с лаговыми переменными (5) и непрерывной модели вида (16). Как уже отмечалось выше, неполное отражение динамических свойств в первую очередь скажется на точности прогноза при других значениях фактора (не используемых при идентификации).
С этой целью для оценки параметров моделей (5) и (16) была использована статистика без последних четырех измерений. Результаты эксперимента показали, что оценки модели (16) практически не изменились, а оценки же лаговой модели изменились существенно:

(21)

Осуществим прогноз по последним четырем наблюдениям объясняющего фактора, т.е. объема ВВП на 1988 – 1991г.г.
На рисунке 5 показаны ошибки прогноза, полученного с помощью этих моделей.

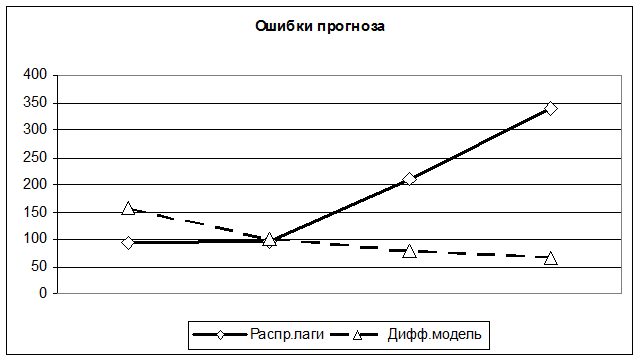
Рисунок 5 – Ошибки прогноза непрерывной и лаговой моделей

Из рисунка видно, что адекватность динамических свойств непрерывной модели гораздо выше, чем модели с распределенными лагами. При этом для непрерывной модели на период прогноза суммарные ошибки составили = 50077, а для лаговой модели = 176547,52.
Оценка параметров динамической модели показала следующее:
1) соответствие модельных и экспериментальных данных является достаточно высоким;
2) моделирование динамических свойств модели является полным. При использовании других значений факторов оценки модели практически не изменились;
3) адекватность динамических свойств модели достаточно высока.
Таким образом, применение динамического моделирования с использованием дифференциальных уравнений помогает избежать проблем, возникающих при использовании лаговой модели, а также дает наиболее точные и достоверные результаты с возможностью прогнозирования. Результаты численного моделирования показали, что предложенный алгоритм идентификации параметров модели достаточно эффективен и может использоваться для оценки динамических свойств экономических процессов.

1. Елисеева И.И., Курышева С.В., Костеева Т.В. и др. Эконометрика / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2007. – С. 298-305
2. Колпаков В.Ф. Параметрическая идентификация модели лесных пожаров // Безопасность жизнедеятельности – 2012. – № 5. – С. 39-44.
3. Синицын И.И. Фильтры Калмана и Пугачева: Учебное пособие. – М.: Университетская книга, Логос, 2006. – С. 320-327

Все статьи автора «eshvyryaeva»