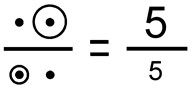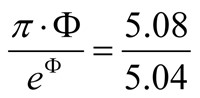This study is devoted to my mother Antonova Zoya Ivanovna, who gave me the life
1. Introduction
This paper is the first step, which presents results of my study of Stonehenge in English. Russian and Latvian people were informed on this study in 90th years by their languages [Zlobin, 1990], [Zlobins,1990]. First of all, I’d like to inform about my scientific level. I graduated from Bauman Moscow State Technical University (BMSTU, Power Engineering Faculty, mechanical engineer, Master degree, 1983) and Lomonosov Moscow State University (MSU, Faculty of Computational Mathematics and Cybernetics, mathematician, Master degree, 1991). In 1992 I obtained scientific degree in BMSTU which corresponds to Ph.D. level. Thus I obtained my education and scientific qualification in best Russian universities. During 15 years I worked in Central Institute of Aviation Motors (CIAM, Moscow). In CIAM I was awarded as winner of competition on best scientific works. My work was connected to aviation gas turbine engines. Aviation engines is well-known branch of high technologies and level of my scientific qualification seems clear. For a long time I investigated hypersonic processes connected to Tunguska meteorite. Simultaneously I had interest to history of Stonehenge and carried out my own study during last 25 years. Below I briefly described main obtained results of the study. I prefer form of description like a diary because this form indicates ways and style of my thinking. There is not necessity to repeat description of general plan of Stonehenge (Fig. 1) because we have excellent publications [Atkinson, 1991], [Hawkins, 1966], [Wood J.E., 1978] and others.
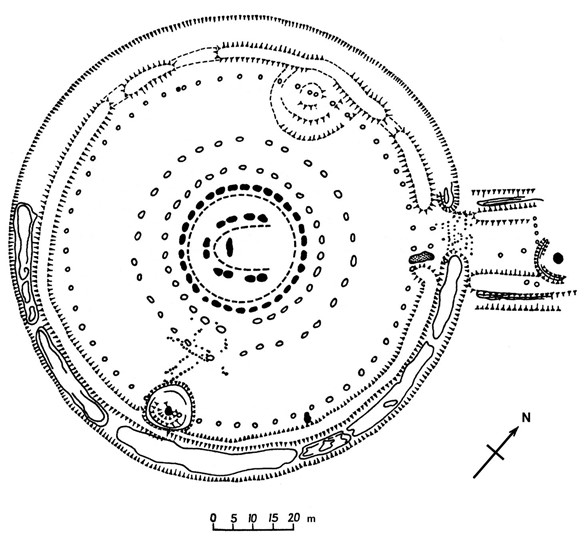
Fig. 1. Plan of Stonehenge in accordance to J.E.Wood, where ancient symbolics is good visible [Wood, 1978]
2. Initial idea
When I made analysis of general plan of Stonehenge for the first time, I compared it with mathematical grid for numerical solution of some partial differential equation. Circular Bank and Circle of Sarsen Stones with lintels were looking like bounds of the grid. Holes X, Y and Z were looking like nodes of the grid. My first guess was that holes were located in accordance to some mathematical law. My first action was absolutely casual but very successful. I resolved Laplace’s partial differential equation with Dirichlet boundary conditions. Ring domain of solution was declared between Circular Bank and Circle of Sarsen Stones with lintels. Boundary conditions were declared as U=10 for Circle of Sarsen Stones with lintels (external border of the Cirle) and U=0 for Circular Bank (internal border of the Bank). Mathematically this task may be written as:
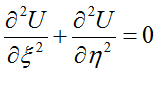 ,
, ![]()
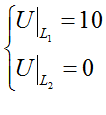
where
L1 – Circle of Sarsen Stones with lintels (external border of the Cirle)
L2 – Circular Bank (internal border of the Bank)
D – ring domain between L1 and L2
All boundary conditions (values) were stated absolutely casual. However, it was luck. The solution is shown in Fig.2. It is good visible that three isolines of solution are in good correspondence to location of Holes X, Y and Z. This solution gave me interesting numbers 8,5,1 which are known as members of Fibonacci sequence of numbers. These three numbers simultaneously gave me hint concerning golden ratio (Ф=1.6180…). For example, 8 over 5 is approximately equal to Ф. Also relation between diameter of ring of X Holes (Aubrey Holes) and diameter of ring of Y Holes approximately equal to Ф too.
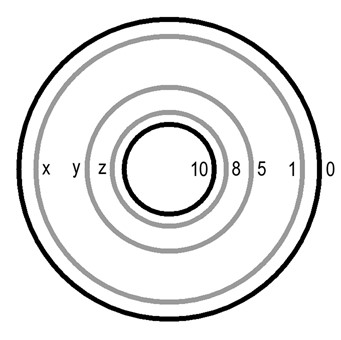
Fig.2. Solution of Laplace’s partial differential equation (rings of Stonehenge) with Dirichlet boundary conditions.
It may be symbolic record of Laplace’s equation and Laplacian
One more hint I understood when wrote the task and solution in another view. If solution of the same task depends only from radius then it may be written as:
differential equation:
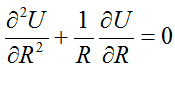
where
![]()
and
R1 – Circle of Sarsen Stones with lintels (external border of the Cirle)
R2 – Circular Bank (internal border of the Bank)
Solution may be written as:
![]()
where coefficients a and b may be found from the system of equations
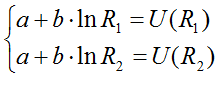
boundary conditions
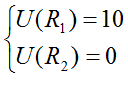
Certainly I noticed that presence of natural logarithm simultaneously gave me the hint concerning Napier number (e=2.7182…). Ring forms reminded me the value of Ludolph number π=3.1415… Let’s remember all these hints.
As a result of all these calculations I supposed that Stonehenge contain some ancient mathematical texts or messages written with ancient symbols. For example, I obtained solution which may be interpreted as record of Laplace’s partial differential equation and record of Laplace’s operator or Laplacian (Fig. 2).
3. Records of partial differential equations
If to look close, we can notice interesting analogy between some modern and ancient mathematical symbols. Let’s look at parallel lines of Avenue of Stonehenge. Parallel lines of Avenue look like sign of equality. In turn Heel Stone indicates the most powerful source for ancient people (Sun). It really looks like Poisson’s equation (Fig.3)
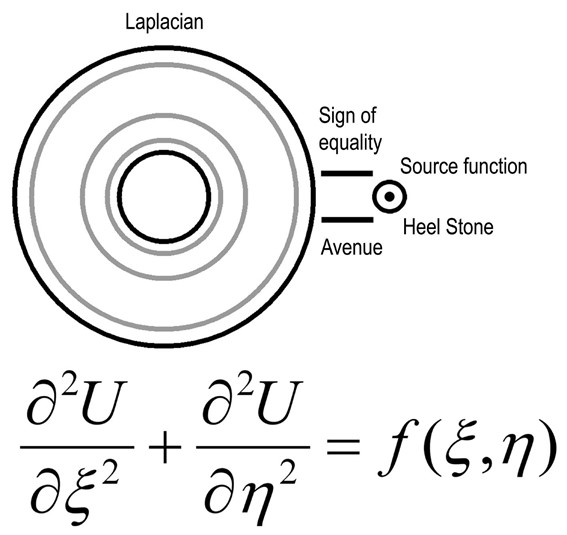
Fig.3. Symbolic record of Poisson’s partial differential equation
As far as I know, we have not clear explanation for Horseshoe of Sarsen Trilithons till now. I’d like to suggest this explanation from position of mathematical significance. Look at Fig.4. where all Sarsen Trilithons are positioned in straight line. G.S.Hawkins already noticed that every Sarsen Trilithon connects to position of Sun or Moon in concrete time [Hawkins, 1966]. Let’s note in addition that Moon Trilithons located between Sun Trilithons. Also Trilithons were manufactured with different altitude [Hawkins, 1966]. If to apply mathematical conception of finite differences, then Horseshoe of Sarsen Trilithons may be interpreted as record of approximate derivatives with respect to time. If to use only Sun Trilithons, then it will be partial derivative with respect to time. If to use Sun Trilithons and Moon Trilithons together, then it will be second partial derivative with respect to time.
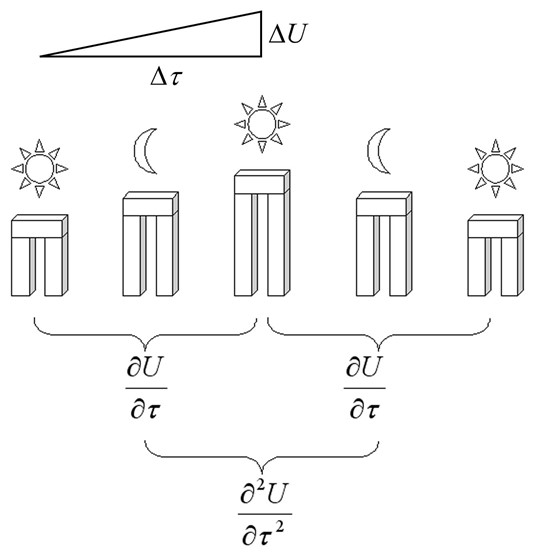
Fig. 4. Approximation of derivatives with respect to time by Horseshoe of Sarsen Trilithons here is shown
One more observation gives us logical connection between Horseshoe of Sarsen Trilithons and rings of Stonehenge. 1) Horseshoe of Sarsen Trilithons was manufactured as stony. Circle of Sarsen Stones with lintels was manufactured as stony too. 2) These two figures are duplicated at general plan of Stonehenge. 3) Both these figures are duplicated with the help of special Bluestones. 4) Both figures are duplicated from internal side of Sarsen stones. 5) In both cases the curve of Sarsen Stones is parallel to the curve of Bluestones. To my mind, builders of Stonehenge had the purpose to repeat many times with these several methods important logical phrase: “Horseshoe of Sarsen Trilithons is equal to Circle of Sarsen Stones with lintel”. It is mathematical sign of equality too. If to use Horseshoe of Sarsen Trilithons as record of partial derivatives then we can read two additional partial differential equations. There are heat equation and wave equation (Fig.5).
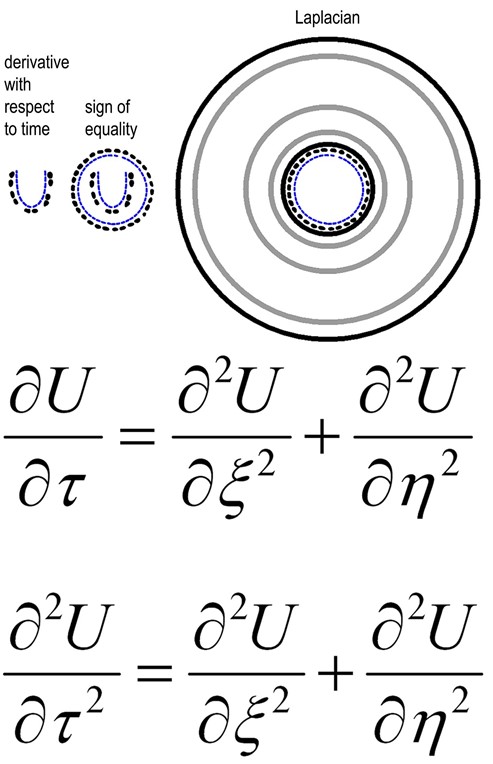
Fig. 5. Symbolic record of heat equation and wave equation (depends on case of derivative with respect to time)
4. Method by J.-F.Champollion and hieroglyphs in Stonehenge
Records of partial differential equations in Stonehenge were very surprise for me. It was absolutely clear that only civilization with high level of scientific development was able to make such records. I decided to check up Egypt as first applicant on these mathematical records. My decision concerning Egypt was confirmed with well-known facts of manufacturing of giant stony structures, such as pyramids. My further study confirmed that I was right on the idea of Egypt.
I decided to check up my first success on differential equations with another methods. First of all, boundary conditions were main subject of my interest. Numbers “10″ and “0″ as boundary conditions were selected absolutely casual in the case of solution of Laplace’s equation. I began to read books about ancient Egyptian mathematics for understanding of style of numbers writing [Struik, 1963], [ Stuchevskiy, 1976]. I was ready to exult when I discovered that Egyptian number “10″ is written with the symbol of horseshoe. It was bright and excellent confirmation of my own logic of decoding. It became clear that Horseshoe of Sarsen Trilithons symbolize Egyptian number “10″ simultaneously with symbol of derivative. Later I understood that every element of Stonehenge is able to symbolize several different ideas. Such property of writing is very convenient for increasing of information density during producing of records. It was not difficult to find one more stony element of Stonehenge connected to solution of Laplace’s equation and coded as symbol “1″. Slaughter Stone is located on the ring of Aubrey Holes (X Holes) and we can see that isoline “1″ of solution of Laplace’s equation coincides with ring of X Holes (Fig. 2). There is good correspondence between Egyptian symbol of number “1″ (single short line) and short line of Slaughter Stone. Confirmation became reliable for boundary conditions for solution of Laplace’s equation. I understood that Egyptians symbols are the key of code of Stonehenge. My further efforts were directed to the study of Stonehenge from position of Egyptian Hieroglyphs.
In accordance to my first success on Egyptian symbols, I supposed that Stonehenge is ancient Egyptian temple of solar god. Certainly I supposed that the name of the god must be written here too. When I understood method of decoding of Egyptian hieroglyphs by J.-F.Champollion [Champollion, 1822], I began to search cartouche and solar symbols on general plan of Stonehenge. I found these all soon. There are two barrows with two Station Stones and the Heel Stone. Every such structure on the plan looks like circle with the point in its center. The same Egyptian hieroglyph symbolize Sun. I recognized as cartouche Circular Bank around Stonehenge . Also I noticed that the beam of sunlight divides Stonehenge on two parts during midsummer sunrise. Simultaneously this beam of sunlight divides Horseshoe of Sarsen Trilithons on two parts. If to take into consideration symbol of Horseshoe as Egyptian “10″ number, then all mentioned symbols looks like some mathematical expression together with sign of equality (Table 1). There is good reason to take into consideration size of every circle with point too. It seems important that circle of North Barrow is larger than circle of South Barrow. We can rewrite the expression as fraction, where numerator look like “big 5″ number and denominator look like “small 5″ number. In this case, Heel Stone must have approximate value of “1″ number. It corresponds well to “1″ value of Slaughter Stone, which is located not far from axis of Stonehenge too. Together with another two Station Stones we can rewrite our expression finally (Table 1 and Fig. 6).
Table 1
|
|
The beam of sunlight divides Horseshoe of Sarsen Trilithons on two parts. The form of horseshoe is Egyptian “10″ number. It is mathematical record, which means division of “10″ number on two parts. |
|
|
There is clear hint concerning four numbers. Two numbers are symbolized by Station Stones. Another two numbers are symbolized by North and South Barrows with Station Stones. Two numbers are located in numerator and two numbers are located in denominator. The circle of North Barrow is larger than the circle of South Barrow. This means that “10″ number is divided on “large five” number (numerator) and “small five” number (denominator). |
|
|
Let us remind hints, which we obtained earlier. I’d like to mention three constants: Ф=1.6180… e=2.7182… π=3.1415… Therefore, it is not difficult to determine values of numerator and denominator. I designated the result of this division as symbol “j” (j=1.0079…). |
Finally obtained mathematical expression can be written as equality:
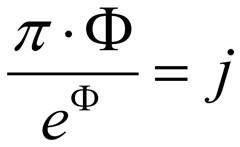
Fig. 6. Mathematical expression which is written in Stonehenge
This mathematical formula looked wonderful. However, where is the name of god here? I was shocked and admired when I understood, that the name of god was recorded numerically. You may check up it by yourself, that the value j= 1.0079… means atomic mass of hydrogen. Thus the name Atom (or Atum) was coded in Stonehenge with the method of mathematical logic and with high mathematical accuracy. Certainly I remember the name of main Egyptian solar god Atum (Atom). Also I remember that Egyptians considered Pharaoh equal to Sun (solar god). Is there anybody, who denies that Sun and man consists mainly from atoms of hydrogen?
Some criticism may be here concerning names of Atom and Atum. Is it possible to equate names of Atom and Atum? Yes, it seems possible. We know from Egyptology that Egyptian records not include vowel letters [Korostovtsev, 1976]. That is why, two names Atom and Atum really are equivalent. Style of writing of this mathematical expression confirm, that we deal with Egyptian symbols. It is well-known from Egyptology that size of hieroglyphs is important for correct understanding of messages [Korostovtsev, 1976]. That is why North Barrow in Stonehenge larger than South Barrow. Also well-known from Egyptology that texts with hieroglyphs were divided on rectangles [Korostovtsev, 1976]. Symmetry was very important too. The same pattern we can see as applied to obtained mathematical expression (Fig. 6 and Fig. 7).
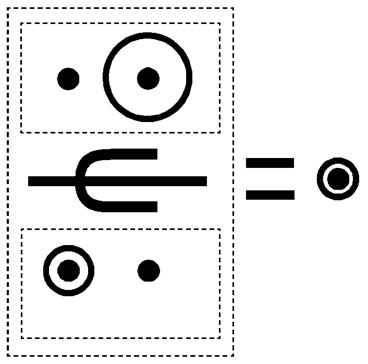
Fig. 7. Rectangular style of Egyptian writing
(secret Egyptian mathematical symbol and rebus “Atum”)
Above I described only one method of writing of the name “Atum”. This method is based on pattern of concrete symbol. However Egyptians duplicated this name in Stonehenge several times with different methods. Below I’d like to describe second method, which based on geometrical relations between rings of X,Y and Z Holes. Builders of Stonehenge inserted one more visual hint for better understanding of second method of writing. I don’t know what kind of objects forms this hint (holes or stones). I see this hint on the plan of Stonehenge in accordance to J.E.Wood (Fig. 1 and Fig. 8). Look at the dotted figure near South Barrow.

Fig. 8. Dotted figure near South Barrow
(pale-grey contour is added by A.E.Zlobin)
To my mind this dotted figure contains a lot of important ideas (Fig. 9). We can see here Egyptian symbol “shen” which mean eternity. The same symbol is well-known as Egyptian cartouche. Also we can see two signs of equality. One sign of equality is directed from ring of Y Holes to South Barrow, and another sign of equality is directed tangential to ring of Z Holes. I think that this symbolism is intended to describe the same mathematical expression with numerator and denominator, which mean the name “Atum”.
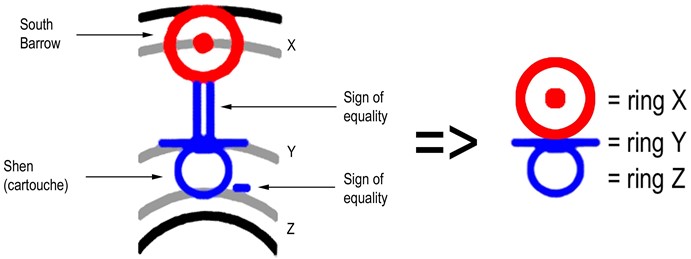
Fig. 9. Explanation of dotted figure near South Barrow
Let’s explain it with more details. The ring of X Holes symbolizes “big five” number and “big ring”:
![]()
The ring of Z Holes symbolizes “small five” number and “small ring”:
![]()
The ring of Y Holes symbolizes result of division (“big five” over “small five”):
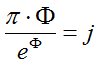
Even astronomical symbolism gives us hints for similar thinking too [Hawkins, 1963, 1966]. For example, North Barrow is connected to summer position of Sun (symbol of “large size of Barrow”). South Barrow is connected to winter position of Sun (symbol of “small size of Barrow”). There is not any doubt, that the name of Atum was duplicated several times with different methods in Stonehenge.
I’d like to describe another ideas concerning dotted figure near South Barrow. To my mind, the circle with the point in its center corresponds to “Sun above horizon” (Sun on the sky), and the circle without point in its center seems as “Sun under horizon” (underground Sun). There is good correspondence to Egyptian mythology about solar god and his underground equivalent as Osiris. Also necessary to note, that the color of unique Altar Stone in Stonehenge was described as pale-green. This color of Altar Stone is explained by a lot of mica dissemination [Hawkins, 1966]. Altar Stone is closer to ring of Z Holes and closer to “shen” symbol too. Is it casual coincidence? In addition, let’s remind about such well-known fact as green color of skin of the god Osiris. Is it casual coincidence too? I think there are a lot of attributes of Egyptian mythology and such coincidences are not casual. As confirmation of my opinion I can note that Horseshoe of Sarsen Trilithons together with Altar Stone simultaneously looks like Egyptian hieroglyph “well” and water in it. We know that Egyptian mythology connects the god Osiris with “fresh water” and “water of River Nile” too [Matie, 1996]. To my mind, here we really have Egyptian message, where gods Atum and Osiris were mentioned together.
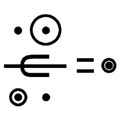
We can make one more interesting conclusion. Symbol “shen” together with long sign of equality looks like Egyptian hieroglyph “ankh” (translation of this symbol is “life”). Therefore, two hieroglyphs (“shen” and “ankh”) may be read together as “Eternally living”. On the background of the name Atum (on the background of three rings of X,Y and Z Holes) this compound hieroglyph gives us clear phrase “Eternally living Atum”. Who was the author of this ancient message? Certainly the sign of the author must be here. To this moment I have already seen a lot of Egyptian symbols and found the sign of author quickly. Look at the pattern of many holes at the Entrance of Stonehenge (Fig 10). Together with Slaughter Stone and holes of “D” and “E” stones, this pattern looks like Egyptian hieroglyph “write”. The form of this hieroglyph repeats form of the device, which scribes used for writing. The style of writing of the hieroglyph seems well corresponds to approximate date 1500 BC. Certainly it is the clearest sign of Egyptian scribe. Simultaneously, it is best confirmation of presence of Egyptian message. Finally we can read full ancient message: “Eternally living Atum. This was written by Egyptian scribe”.
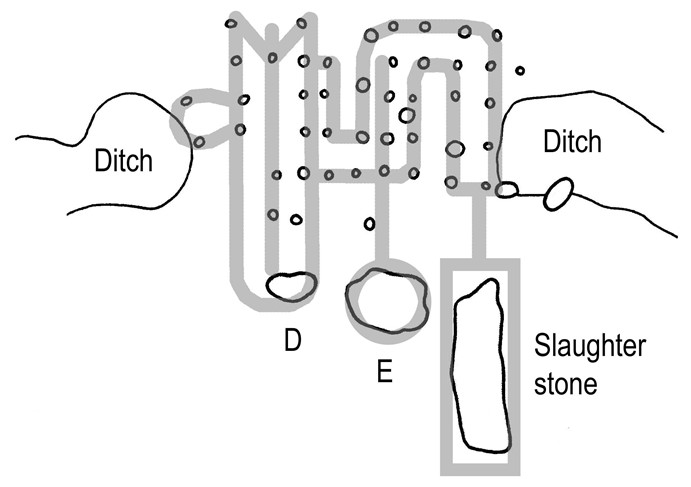
Fig. 10. Egyptian hieroglyph “write” in the form of the device for writing (pale-grey contour is added by A.E.Zlobin). The picture in accordance to [Wood, 1978]
5. Egyptian vocabulary of Stonehenge
Below I collected all symbols and hieroglyphs in common vocabulary of Stonehenge (Table 2). Also I illustrated all Egyptian symbols on the scheme of Stonehenge (Fig. 11).
Table 2
| Symbol |
Objects on the plan of Stonehenge |
Translation (explanation) |
 |
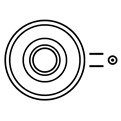
Circular Bank | Sacred symbol like cartouche. It indicates that the element of Stonehege or its internal symbols are related to the name of god or sacred secret |
 |
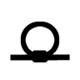
North Barrow, South Barrow with Station Stones and ditches, Heel Stone with ditch | Egyptian hieroglyph which means “Sun”. Simultaneously it means some numerical value. Size of the symbol approximately indicates value of number (large or small number) |
 |
A part of dotted figure near South Barrow | Egyptian hieroglyph “shen” which means “eternity”. Also this hieroglyph well-known as cartouche |
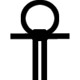 |
Compound dotted figure near South Barrow | Compound Egyptian hieroglyph “ankh” which means “life”. Together with included hieroglyph “shen” it means “eternally living” |
 |
Horseshoe of Sarsen Trilithons together with Altar Stone | Egyptian symbol which means “well with water” |
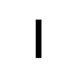 |
Slaughter Stone | Egyptian mathematical symbol which means “1″ number |
 |
Horseshoe of Sarsen Trilithons | Egyptian mathematical symbol which means “10″ number |
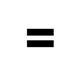 |
Avenue, parallel curves which consists of Bluestones, parallel dotted lines near South Barrow | In Stonehenge it means mathematical or logical “sign of equality” |
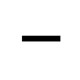 |
Beam of sunlight during midsummer sunrise, horizontal line in the “shen” symbol | Mathematical symbol of division. Symbols above this line means numerator. Symbols below this line means denominator |
 |
The pattern of many holes at the Entrance of Stonehenge together with Slaughter Stone and Holes of stones “D” and “E” | Egyptian hieroglyph “write” in the form of the device for writing. This device was used by every Egyptian scribe |
 |
North Barrow, South Barrow, Heel Stone, Station Stones, Avenue, Beam of sunlight during midsummer sunrise | Sacred symbol, rebus and mathematical formula which means atomic mass of Hydrogen and the name of the god Atum (Atom) simultaneously |
 |
Circular Bank, rings of X,Y and Z Holes, Circle of Sarsen Stones with lintels | Mathematical symbol which means Laplace’s partial differential equation and Laplacian simultaneously |
 |
Circular Bank, rings of X,Y and Z Holes, Circle of Sarsen Stones with lintels, Heel Stone, Avenue | Mathematical symbol which means Poisson’s partial differential equation |
 |
Circular Bank, rings of X,Y and Z Holes, Circle of Sarsen Stones with lintels, Horseshoe of Sarsen Trilithons, Bluestones | Mathematical symbol which means Wave partial differential equation or Heat partial differential equation (depends on case of derivative with respect to time) |
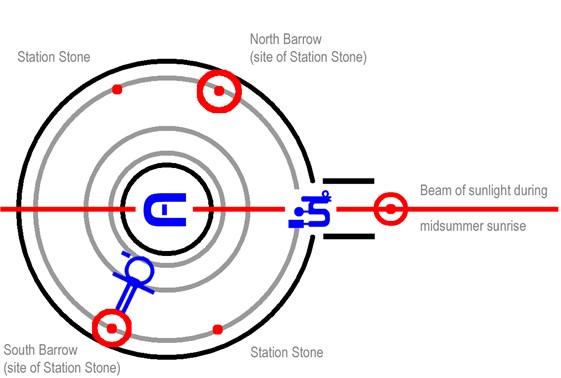
Fig. 11. Egyptian symbols and hieroglyphs on the scheme of Stonehenge
6. Method of building of Stonehenge
Builders of Stonehenge gave us very clear hints concerning method of its manufacturing. I have already mentioned that Horseshoe of Sarsen Trilithons looks like Egyptian symbol “well with water”. Stone “E” in hieroglyph “write” symbolize “vessel with water”. The vessel is included to the Egyptian device for writing. Both these symbols of water are located near axis of Stonehenge and seems symbolize direction of water flow. Also well-known that Avenue of Stonehenge leads eventually to the bank of the River Avon [Atkinson, 1991]. Let’s remind that Egyptians had giant experience of irrigation works and manufacturing of irrigation systems. They were being producing man-made channels, lakes, banks, dams and other systems for control of water. Devices for lifting of water level like shadoof and gateway were used by Egyptians too. I thought a lot. If it will be necessary for me to build Stonehenge, what method I’ll select? To my mind, water technologies of Egyptians were used during manufacturing of Stonehenge and lifting of giant stones were made with the help of hydraulics. As engineer, I prefer this method of lifting of heavy cargo instead of using of hands. G.S.Hawkins mentioned interesting experiment in his book. A model of stone was located on a raft for transporting by water. It was noted that even a child can control this process with the help of long stick [Hawkins, 1966]. I consider that stones were transported to Stonehenge by method of shipping with the help of rafts and pontons. Then several circular banks or walls were manufactured for organizing of man-made basins in the area of Stonehenge (Fig. 12). The wall of every internal basin was some higher than the wall of external basin.
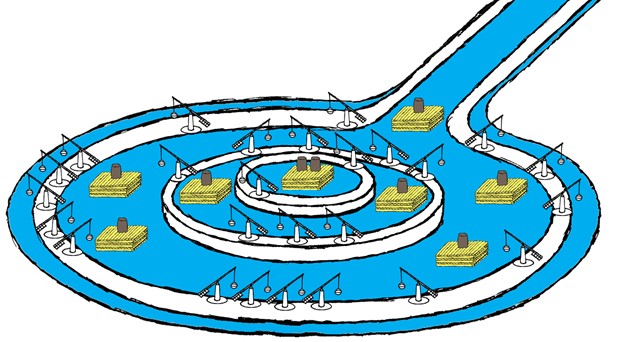
Fig. 12. Scheme of man-made basins and hydraulic method of manufacturing of Stonehenge.
For clearer picture not all devices (pontons and shadoofs) are shown here. Size of devices is increased a little too.
The opinion is known that level of water was increased in River Avon with the help of dam [Hawkins, 1966]. Water flow was turned from the River Avon with the help of Avenue channel. Water exchange between man-made basins was organized with the help of many devices like shadoof. Stones were built-in into wooden pontons not far from target places. With the help of shadoofs the level of water was increased and stones were simply transported by pontons to target places. Then the level of water was decreased and all stones were fixed on target places. This method explains manufacturing of Stonehenge including lifting by hydraulic method of lintels stones. Holes of rings X,Y and Z seems not only informational structures, but seems places for location of shadoofs too. Internal banks or walls were deleted later. A lot of holes at the entrance of Stonehenge looks like contour of water gateway device and contour of symbol “write” simultaneously. Once again, it is wonderful confirmation of high intellect of builders of Stonehenge. They were able to achieve a lot of targets simultaneously.
7. Conclusion
I am not Egyptologist, not historian and not archaeologist. I am mathematician and engineer. Applications of Stonehenge are interesting for me. The purpose of my study was to understand code of Stonehenge and to explain method of building this stony monument. It seems I have success on this activity. I confirm that astronomical directions in Stonehenge were selected not casual. The idea about astronomical directions in Stonehenge was useful [N.J. Lockyer, 1906]. G.S.Hawkins really made great discovery when he found astronomical directions connected to positions of Sun and Moon. Moreover, these directions are not only confirmation of Stonehenge as ancient observatory. It is wonderful method for recording of important knowledge on mathematics and physics. I understood and decoded ancient style of writing of differential partial equations. Also I decoded the name of ancient Egyptian god Atum (Atom) which was coded with the help of hieroglyphs and numbers. The most ancient theory of Atom of Hydrogen was coded in Stonehenge too. I must note especially that nobody of modern mathematicians and physicists know mathematical formula for atomic mass of Hydrogen in the form of Egyptian record. This formula was unknown for all scientists till now. Secret method of writing of Egyptian sacred knowledge with the help of mathematics was not known too. Thus we obtained possibility to investigate Egyptian records from position of most sacred secrets.
The most interesting fact is that Atom of Hydrogen contains logical idea in the form of wonderful mathematical expression. Is it main reason for Egyptians to recognize Atom as god and base of life? “As the result of excavations we can now divide the history of Stonehenge into several periods, covering a span of about twenty centuries between about 3100 and 1100 BC” [Atkinson, 1991]. Style of hieroglyph “write” (Fig. 10) indicates the date of manufacturing of Stonehenge. The style approximately corresponds to the date 1500 BC. It is third phase of Stonehenge (end of great monuments). There is good agreement between style of writing of the hieroglyph and result of excavations. I’d like to note that epoch of Pharaoh Akhnaton is not far from this date. Is it possible to suppose that reforms of Pharaoh Akhnaton were prepared in Stonehenge? Is it possible to consider Stonehenge as distant experimental place for scheduling of such reforms? Certainly, there are only my assumptions and only high qualified experts in Egyptology can confirm or reject these ideas.
I try to answer the question concerning all applications of Stonehenge. I think it was ancient Egyptian solar temple of the god Atum. G.S.Hawkins determined Stonehenge as ancient observatory and neolithic computer simultaneously. I agree to these conclusions by G.S.Hawkins too. Also I compare Stonehenge with giant stony computer diskette, which contains important scientific information. Positions of Sun and Moon gives us possibility to read information from this diskette. Most of all Stonehenge remind me ancient Egyptian distant center of science and higher education. It is very interesting for me to consider Stonehenge as the most ancient University. I not exclude that Stonehenge University was the first center of higher education in ancient England. I know about so-called “houses of life” in ancient Egypt which are mentioned as higher schools [Korostovtsev, 1976]. To my mind Stonehenge is the best confirmation of reality of such Universities.
We know that ancient Egyptians used mathematics in their practice [Struik, 1963], [Stuchevskiy, 1976]. Somebody may ask me about application of partial differential equations in ancient Egypt. I think it was military application first of all. Stonehenge with man-made basins even looks like fortification. I not exclude that Stonehenge was ancient Military University simultaneously. It is well-known that today partial differential equations are used for forecasting in military activity [Chuev et al., 1975 ]. To my mind military power of ancient Egypt was supported with higher education and possibility of forecasting of results of wars. It was mathematics of numerical methods which mean repeated usage of simple algorithms. That is why all similar prehistoric monuments looks like mathematical grid for numerical methods. For example, let’s remind not only Stonehenge but also Carnac Stones in Brittany. All these monuments connect to positions of Sun or Moon for the purpose of working like computer timer. Astronomical time was necessary for working of these giant stony processors. Sun or Moon worked as devices for realizing of clock rate in computers. A lot of people were located between nodes of neolithic mathematical grid and they followed commands of priests. Every command looked like very simple arithmetical action. For example, small stones or grains were distributed as fifty-fifty between neighbour men during one cycle. Certainly only Egyptian priests were able to understand the result of all cycles of calculations. I not exclude, that these calculations were presented by priests to people like dialogue with god.
Let’s look through simple example. Let’s locate four points (nodes) in some distance from each other in the form of cross. We will calculate value in fifth central point as arithmetical average between another four points. Is it difficult? No certainly. Even a child is able to carry out such calculation. However, with this algorithm we realized numerical method of solution of two-dimensional partial differential equation of Laplace. If to repeat this algorithm many times in all internal nodes of grid we will obtain solution of Laplace’s equation in full domain of calculations. I think solution of Laplace’s partial differential equation was necessary for purposes of irrigation works in Egypt. For example, Laplace’s equation describes steady distribution of water flow.
Here I not mention accuracy of my mathematical calculations in Stonehenge. I see wonderful mathematical logic in Stonehenge and I understand logical style of ancient message. The accuracy of my calculations seems not important subject in this case. Moreover, some information was duplicated in Stonehenge. This gives me reliance concerning correctness of my decoding. I can not determine origin of Egyptian higher mathematics. I can not explain knowledge of atomic mass of Hydrogen by ancient Egyptians. I can only suppose that several thousand years of Egyptian history gave ancient men time for prolonged thinking and for prolonged numerical calculations. To my mind, we have confirmation that mathematics of ancient Egyptians was based mainly on numerical methods. I see symbols of mathematical finite differences. I know that the most difficult tasks of today are resolved with numerical methods too.
I’d like to note that not only Stonehenge but also Egyptian temple was close investigated by G.S.Hawkins [Hawkins, 1973]. Today we know about very interesting results of the Stonehenge Hidden Landscapes Project [Gaffney et al., 2012]. I hope new studies will give us more information about real history of Stonehenge. Is it possible to use knowledge of ancient Egyptians in modern science? I think it is possible. I already delivered several publications about unique properties of mathematical formula of atom of Hydrogen [Zlobin, 2010], [Zlobin, 2014]. To my mind there are a lot of analogies with ideas of V.I.Vernadsky concerning origin of life. It is important, that mathematical logic is discovered as property of atom. To my mind we can use this property for better understanding of problem of artificial intelligence.
Acknowledgments
I very thankful to Dr. V.S.Komissarov who initiated my interest concerning Stonehenge. Also I very thankful to Dr. V.K.Zhuravlyov who urgently sent for me two wonderful books about Stonehenge. I thankful to all people who are interested on study of Stonehenge and who saved Stonehenge from destructive influence of time.
References
- Atkinson R.J.C. 1991, Stonehenge and Neighbouring Monuments. English Heritage. Fourth impression, London.
- Champollion, J.-F. 1822, About Egyptian hieroglyphic alphabet. Translation, edition and comments by Lifshits I.G. [in Russian]. Publishing house of Academy of Sciences of USSR, Leningrad. 1950.
- Chuev, Yu.V., Mikhaylov, Yu.B. 1975, Forecasting in military activity [in Russian]. Press House of Ministry of Defence of USSR, Moscow.
- Gaffney, C., Gaffney, V., Neubauer, W., Baldwin, E., Chapman, H., Garwood, P., Moulden, H., Sparrow, T., Bates, R., Löcker, K., Hinterleitner, A., Trinks, I., Nau, E., Zitz, T., Floery, S., Verhoeven, G., Doneus, M., 2012, The Stonehenge Hidden Landscapes Project. Archaeological Prospection. Volume 19, Issue 2, April/June 2012, Pages: 147-155.
- Hawkins, G.S., 1963, Stonehenge decoded. Nature, 200, 306-308.
- Hawkins, G.S., 1964, Stonehenge: a Neolithic computer. Nature, 202, 1258-1261.
- Hawkins, G.S., White J.B. 1966, Stonehenge Decoded. Published by Souvenir Press, London. Translation by Gurov P.S. with edition by Gurshteyn A.A. [in Russian]. “Mir” Press, Moscow, 1984.
- Hawkins, G.S., 1973, Beyond Stonehenge. Harper & Row, Publishers New York, Evanston, San Francisco, London. Translation by Gurov P. with edition by Gurshteyn A. [in Russian]. “Mir” Press, Moscow, 1977.
- Korostovtsev M.A. 1976, Language and writing of ancient Egyptians [in Russian] / Culture of ancient Egypt, Institute of Oriental Studies, Academy of Sciences of USSR, Nauka Press, Moscow, 290-304.
- Korostovtsev M.A. 1976, Religion [in Russian] / Culture of ancient Egypt Institute of Oriental Studies, Academy of Sciences of USSR, Nauka Press, Moscow, 180-222.
- Korostovtsev M.A. 1976, Scribes, schools, libraries [in Russian] / Culture of ancient Egypt, Institute of Oriental Studies, Academy of Sciences of USSR, Nauka Press, Moscow, 305-314.
- Lockyer, N.J., 1906, Stonehenge and other British Stone Monuments Astronomically Considered, Macmillan, London.
- Matie, M.E., 1996, The elected studies on mythology and ideology of ancient Egypt [in Russian]. Institute of Oriental Studies, Russian Academy of Sciences. Eastern Literature Press (RAS), Moscow.
- Struik D.J. 1963, Abriss der geschichte der mathematik. Veb Deutscher Verlag Der Wissenschaften, Berlin. Brief review of history of mathematics. Translation by Pogrebysskiy I.B. [in Russian]. Nauka Press, Moscow, 1978.
- Stuchevskiy I.A. 1976, Scientific way of thinking in ancient Egypt / Culture of ancient Egypt, Institute of Oriental Studies, Academy of Sciences of USSR, Nauka Press, Moscow, 250-278.
- Wood J.E. 1978, Sun, moon, and standing stones. Oxford University Press. Oxford, London, New York. Translation by Gurov P.S. with edition by Gurshteyn A.A. [in Russian]. “Mir” Press, Moscow, 1981.
- Zlobin A.E. 1990, Stonehenge: Partial differential equations of mathematical physics (Bauman Moscow State Technical University). [in Russian]. Science and We, No. 5, 20-21.
- Zlobins A.E. 1990, Stounhendža un diferenciāl-vienādojumi (Baumana Maskvas Valsts tehniskā universitāte). [in Latvian]. Zinātne un Mēs, Nr. 5, 20-21.
- Zlobin, A.E. 2010, Atom of hydrogen as a metric base in organic world. Abstract of 2-nd International Congress-Partnering & Exhibition on Biotechnology and Bioenergy (EurasiaBio-2010). April 13-15, WTC, Moscow, 410-411.
- Zlobin, A.E. 2010, Mathematical metrics of atom of hydrogen as biological and philosophical factor [in Russian]. Abstract of 4-th annual scientific-practical conference «Philosophical problems of biology and medicine», volume 4, «Fundamental and applied» held on October 27-28, 2010 at the Institute of Philosophy of Russian Academy of Sciences, Publ. Printberry, Moscow, 117-120.
- Zlobin, A.E. 2014, Symmetry infringement in mathematical metrics of hydrogen atom as illustration of ideas by V.I.Vernadsky concerning origin of life and biosphere. Acta Naturae, Special issue, No. 1, p.48.