По проведенному swot-анализ конкурирующих компаний компании «Coca-Cola» и «PepsiCo»[1] получены две матрицы сравнения: С- для компании Coca-Cola, а Р – для компании PepsiCo. Применим теорию игр для определения наилучшей стратегии:
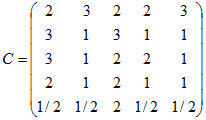
Нормализуем данные матрицы путём деления каждого элемента матрицы на сумму элементов в столбце. Найдем относительные веса полученных нормализованных матриц.
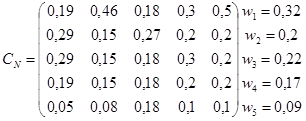
Найдём коэффициенты a и Я для матриц СN и РN соответственно, как средние значения относительных весов.
.gif){kind=small}
Добавим полученные коэффициенты a и Я в ранее полученные регрессионные уравнения аддитивной и мультипликативной моделей соответственно [2]:
.gif){kind=small}
Тогда получим платёжную матрицу игры для двух компаний:
Выполним проверку на наличие седловой точки.
Игрок 1 выберет стратегию, обеспечивающую максимальный выигрыш, тогда игрок 2 определит стратегию, мимнимизирующую выигрыш игрока I. Тогда
.gif)
Тогда гарантированный выигрыш, определяемый нижней ценой игры .gif){kind=small}
, которая указывает на максимальную чистую стратегию, и определяем верхнюю цену игры .gif){kind=small}
.
Поскольку верхняя и нижняя цены равны, следовательно, стратегии устойчивы, т.е. каждый игрок должен придерживаться своей стратегии и любое отклонение от неё ухудшит положение фирмы. При этом чистая цена игры (седловая точка или выигрыш) равна 11.3895.
Наличие седловой точки позволит утверждать, что фирмам выгодно придерживаться своих стратегий.
Для оценки стратегии каждой компании решим эту же игру в смешанных стратегиях геометрическим методом.
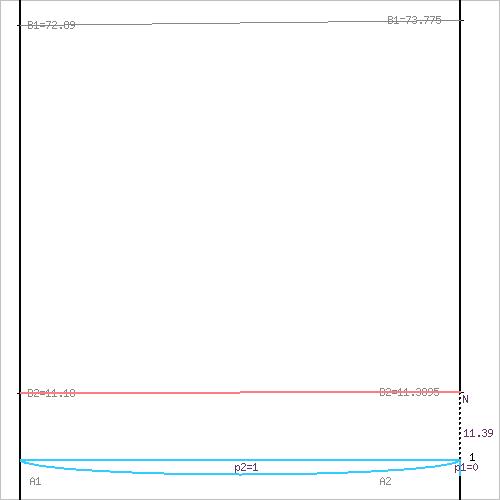
Графическое решение игры представлено на рисунке 1.
Рисунок 1 – Решение матричной игры графическим методом.
Максиминной оптимальной стратегии игрока A соответствует точка N, для которой можно записать следующую систему уравнений:
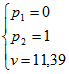
Теперь можно найти минимаксную стратегию игрока B, записав соответствующую систему уравнений, исключив стратегию B1, которая дает явно больший проигрыш игроку B, и, следовательно,
.gif)
Ответ:
Цена игры: v = 11.39, векторы стратегии игроков: Q(0, 1), P(0, 1)
Выполним проверку решения игры на основе критерия оптимальности стратегии.
.gif)
Данный критерий подтверждает правильность решения.
Проведенный анализ доказывает, что борьба между компаниями PepsiCo и Coca-Cola будет длиться до тех пор пока одна из них не сойдет добровольно с дистанции. Каждый рекламный ход одной компании незамедлительно действует на продажи другой, поэтому они обязаны отвечать на рекламные вызовы друг друга, именно поэтому их рекламные бюджет из года в год становятся все больше и они ищут новые способы привлечения и удержания своих потребителей. Полученные данные подтверждает и маркетинговые исследования борьбы двух мировых корпораций.
Библиографический список
- Зеленина Л.И., Трофимова Е.В. Исследование механизма влияния рекламной деятельности конкурирующих компаний.// Гуманитарные научные исследования. 2015. № 7 [Электронный ресурс]. URL: http://human.snauka.ru/ 2015/07/12098 (дата обращения: 07.08.2015)
- Зеленина Л.И., Трофимова Е.В. Моделирование деятельности конкурирующих компаний на основе адаптивных моделей прогнозирования// Современные научные исследования и инновации. 2015. № 7 [Электронный ресурс]. URL: http://web.snauka.ru/ issues/2015/07/56542 (дата обращения: 07.08.2015).
- Соколова А.С., Зеленина Л.И. Имитационное моделирование как конструктивный метод принятия управленческих решений // Инноватика: научный электронный журнал. – 2014, №2. – Санкт-Петербург: ООО ИННОВАТИКА, 2014. – ЭЛ № ФС 77-57224, ISSN 2312-2765, с.47-55
- Федькушова С.И., Зеленина Л.И. Оптимизация управленческих решений на основе информационных технологий // Психология, социология и педагогика. 2015. № 1 (40) стр. 4-9 [Электронный ресурс]. URL: http://psychology.snauka.ru/2015/01/3877 (дата обращения: 01.01.2015).
- Олар Я.В., Зеленина Л.И. Теория игр как эффективный метод разработки управленческих решений// Психология, социология и педагогика. 2015. № 5 [Электронный ресурс]. URL: http://psychology.snauka.ru/2015/05/4890 (дата обращения: 16.06.2015).
- Пантелеева Е.В., Зеленина Л.И. Регрессионный анализ как продуктивный метод исследования статистических данных // Современная педагогика. 2015. № 5 [Электронный ресурс]. URL: http://pedagogika.snauka.ru/2015/05/4280 (дата обращения: 01.07.2015).