Введение
Согласно теории относительности, часы, синхронные в собственной инерциальной системе отсчета, где они неподвижны, – с точки зрения движущегося относительно них со скоростью V наблюдателя в общем случае идут не синхронно. Это означает, что часы в точках A и B показывают разное время, отличающееся на величину ∆t0, которая дается выражением [1 с.17; 2 с.68-69; 3 с.62]:
∆t0 = γ∙V∙Δx/c2
где: γ = (1 – V 2/c2) –1/2 – Лоренц-фактор; Δx – проекция расстояния между часами в системе отсчета наблюдателя на прямую, параллельную скорости V; с – скорость света.
В системе отсчета этого наблюдателя, вследствие Лоренцева сокращения, величина Δx в γ раз меньше величины Δx0, представляющей собой проекцию расстояния между часами на прямую, параллельную скорости V, но в системе отсчета, где эти часы неподвижны. Поэтому предыдущее уравнение эквивалентно следующему:
∆t0 = V∙Δx0/c2 (1)
Причем, для наблюдателя отстают (показывают меньшее на ∆t0 время) часы, движущиеся с его точки зрения впереди.
Следствия релятивистской одновременности
Исследуем ход неподвижных часов с точки зрения движущегося наблюдателя, при изменении им своей скорости (т.е. при его переходе в другую инерциальную систему отсчета), но в рамках специальной теории относительности. Пусть в неподвижной системе отсчета в точках A и B, расстояние между которыми равно Δx0, расположены идентичные и синхронные часы. Наблюдатель движется вдоль прямой AB с постоянной скоростью V. Причем вначале он находится за границами отрезка AB и в процессе своего движения первыми встречает часы в точке B (рис. 1).
 Рис. 1. Наблюдатель начинает и заканчивает разворот в непосредственной близости от точки B внутри отрезка AB, поэтому при совмещении с часами B он движется инерциально.
Рис. 1. Наблюдатель начинает и заканчивает разворот в непосредственной близости от точки B внутри отрезка AB, поэтому при совмещении с часами B он движется инерциально.
В момент совмещения с точкой B наблюдатель фиксирует на часах B время t1. С точки зрения наблюдателя, в момент его совмещения с точкой B, часы в точке A опережают часы в точке B, и в соответствии с (1), имеют следующие показания:
τ1 = t1 + V∙Δx0/c2
Сразу после встречи с часами B наблюдатель включает двигатели и разворачивается путем торможения и последующего разгона в обратную сторону с постоянным ускорением a. Когда на обратном пути непосредственно перед встречей с точкой B он достигает скорости –V, то выключает двигатели (его движение становится инерциальным). После этого, в момент совмещения с точкой B, наблюдатель фиксирует на часах B время t2. Теперь для него часы в точке A отстают от часов в точке B, и согласно (1), имеют следующие показания:
τ2 = t2 – V∙Δx0/c2
Сколько времени с точки зрения наблюдателя отсчитали часы A пока он разворачивался? Чтобы найти это время вычтем показания часов A перед разворотом из их показаний после разворота, в результате получим:
τ2 – τ1 = t2 – t1 – 2∙V∙Δx0/c2
Заметим, что t2 – t1 это время разворота наблюдателя по часам B, т.е. время, которое затратил наблюдатель на разворот с точки зрения неподвижной системы отсчета. Учитывая, что ускорение наблюдателя в неподвижной системе отсчета постоянно, это время равно:
t2 – t1 = 2∙V/a
Подставляя полученное значение в предыдущее уравнение, получим:
τ2 – τ1 = 2∙V/a – 2∙V∙Δx0/c2
Если при этом выполняется неравенство:
2∙V/a < 2∙V∙Δx0/c2,
то τ2 < τ1. В этом случае с точки зрения наблюдателя (опирающегося на специальную теорию относительности) пока он разворачивался, часы A ушли назад. Проверим, может ли полученное нами неравенство быть истинным. Преобразовав его получим:
a∙Δx0/c2 > 1
Очевидно, что при достаточно большой величине a и/или Δx0, это неравенство будет истинно. Оценим при каких значениях a и Δx0 выражение a∙Δx0/c2 будет равно единице. Пусть ускорение a равно 106 м/с2, что примерно соответствует ускорению пули в стволе огнестрельного оружия, тогда:
Δx0 ≈ 9∙1010 м. = 90 млн. км.
Это меньше чем расстояние от Солнца до Земли. То есть с точки зрения пули, выпущенной на Земле, пока она летела в стволе – время на Солнце шло вспять.
Если в точке A происходит непрерывная причинно-связанная последовательность событий, то, очевидно, что событие X1, произошедшее в момент времени τ1 является причиной события X2, произошедшего в момент времени τ2, но с точки зрения наблюдателя событие X2 может наступить раньше X1 (если a∙Δx0/c2 > 1). Причем для наблюдателя эти события происходят с одним и тем же телом в точке A, что не может соответствовать действительности [4 с.156-163].
Возможность экспериментального подтверждения
Мы получили, что согласно теории относительности, при развороте наблюдателя время в окрестности точки A может испытывать инверсию, т.е. идти вспять. Т.к. это противоречит принципу причинности, то встает вопрос – можно ли получить экспериментальное подтверждение данному эффекту? Оказывается, можно.
Рассмотрим следующий мысленный эксперимент. Пусть в некоторой инерциальной системе отсчета (ИСО) покоится длинный жесткий стержень. На одном конце этого стержня расположен излучатель фотонов, а на другом – зеркало. Вдоль прямой, на которой лежит этот стержень, летит наблюдатель со скоростью, равной половине скорости света (0,5c). Наблюдатель подлетает к стержню со стороны излучателя. Когда наблюдатель и излучатель совмещаются, то излучатель испускает в сторону зеркала фотон. Фотон летит до зеркала, отражается от него и возвращается к излучателю. Наблюдатель летит ровно до середины стержня, быстро меняет свою скорость на противоположную и тоже летит обратно к излучателю (Рис. 2). Для простоты условимся, что ускорение наблюдателя при развороте сколь угодно большое. Это позволит нам не учитывать собственное время наблюдателя, затраченное им на разворот.
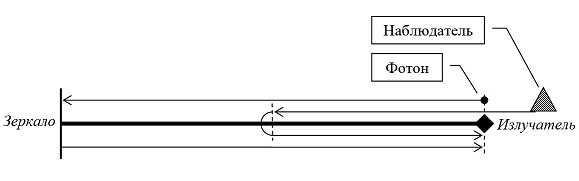 Рис. 2. ИСО, в которой стержень неподвижен.
Рис. 2. ИСО, в которой стержень неподвижен.
Таким образом, в нашей неподвижной ИСО имеем следующую ситуацию. Скорость наблюдателя в 2 раза меньше световой, но и расстояние, которое преодолевает наблюдатель в 2 раза меньше. Следовательно, наблюдатель и фотон на обратном пути встретятся у излучателя.
Посмотрим теперь на весь процесс глазами нашего наблюдателя. Наблюдатель не может непосредственно наблюдать фотон, но он учился в школе и может рассчитать положение фотона относительно стержня. Давайте проделаем этот несложный расчет и найдем положение фотона с точки зрения наблюдателя, непосредственно перед его разворотом и после.
Во время своего движения до разворота наблюдатель находится в ИСО, в которой стержень движется в его сторону со скоростью 0,5c. Когда излучатель совместился с наблюдателем – в сторону зеркала был испущен фотон (Рис. 3). В этот момент:
1. Расстояние между фотоном и зеркалом равно длине стержня, а скорость их сближения равна 1,5c.
2. Расстояние между наблюдателем и серединой стержня равно половине длины стержня, а скорость их сближения равна 0,5c.
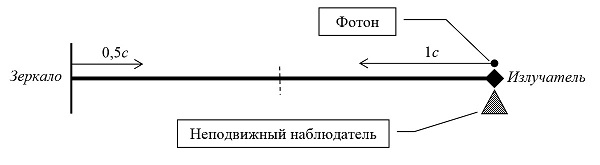 Рис. 3. ИСО, в которой наблюдатель до начала разворота неподвижен.
Рис. 3. ИСО, в которой наблюдатель до начала разворота неподвижен.
Мы видим, что расстояние между фотоном и зеркалом в 2 раза больше расстояния между наблюдателем и серединой стержня, но фотон сближается с зеркалом в 3 раза быстрее, чем наблюдатель с серединой стержня. Следовательно, фотон и зеркало встретятся раньше, чем наблюдатель и середина стержня, т.е. к тому моменту времени (по часам наблюдателя) когда середина стержня достигла наблюдателя, фотон уже отразился от зеркала. Пусть, для наглядности, зеркало сразу же после отражения фотона самоликвидируется (взрывается).
Теперь посмотрим, где должен находиться фотон с точки зрения наблюдателя сразу после его разворота. Сразу после разворота наблюдатель находится в ИСО, в которой стержень движется с той же скоростью, но уже в другую сторону (Рис. 4). В этот момент:
1. Расстояние между наблюдателем и излучателем равно половине длины стержня и уменьшается со скоростью 0,5c.
2. Предположим, что фотон уже отразился и зеркало разбито, тогда расстояние между фотоном и излучателем равно (или меньше) длины стержня и уменьшается со скоростью 1,5c.
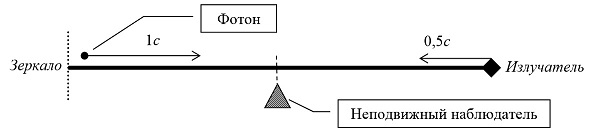 Рис. 4. Инерциальная система отсчета, в которой наблюдатель неподвижен после разворота.
Рис. 4. Инерциальная система отсчета, в которой наблюдатель неподвижен после разворота.
Мы видим, что в этом случае фотон находится от излучателя на расстоянии в 2 раза большем (или еще ближе), чем наблюдатель, а сближается фотон с излучателем в 3 раза быстрее, чем наблюдатель. Следовательно, фотон и наблюдатель не встретятся у излучателя, раньше к излучателю прибудет фотон, причем с большим опережением. Но этого быть не может, фотон и наблюдатель должны встретиться у излучателя. Значит наше предположение о том, что фотон уже отразился от зеркала ошибочно, т.е. к тому моменту времени (по часам наблюдателя) когда наблюдатель только что завершил разворот (перестал испытывать что-то похожее на гравитационное поле), фотон не мог еще отразиться, и зеркало еще цело.
Получаем, что непосредственно перед разворотом наблюдатель совершенно убежден, что зеркало уже разбито. Однако сразу после разворота он вынужден заключить, что зеркало цело. Это может быть только в том случае, если зеркало за время разворота наблюдателя в нарушение принципа причинности само собралось из осколков.
Результат этого эксперимента позволяет наблюдателю сделать только два вывода:
- Релятивистский постулат о постоянстве скорости света ошибочен.
- На участке разворота время в окрестности зеркала реально шло вспять.
Выбор не богатый, но какой из этих двух вариантов больше соответствует действительности, на наш взгляд, очевидно.
Заключение
Приведенный выше анализ доказывает противоречивость релятивистских принципов постоянства скорости света и относительности одновременности, которые являются фундаментом теории относительности. Ключевую роль и неразрывную взаимосвязь этих принципов для своей теории подчеркивал сам Эйнштейн, цитата [5 c.418]: «Оказывается, что принцип постоянства скорости света и принцип относительности противоречат один другому только до тех пор, пока сохраняется постулат абсолютного времени, т.е. абсолютный смысл одновременности. Если же допускается относительность времени, то оба принципа оказываются совместимыми; в этом случае, исходя из этих двух принципов, получается теория, называемая «теорией относительности».
Библиографический список
- Фейнман Р., Лейтон Р., Сэндс М. Фейнмановские лекции по физике. В 9 т. Т.II. Пространство, время, движение. – М.: МИР, 1965
- Угаров В.А. Специальная теория относительности. – 2-е изд., испр. – М.: НАУКА, 1977
- Фок В.А. Теория пространства, времени и тяготения. – 2-е изд., дополненное. – М.: Государственное издательство физико-математической литературы, 1961
- Рейхенбах Г. Философия пространства и времени, перевод с английского Ю.Б. Молчанова, общая редакция А.А. Логунова. – М.: Прогресс, 1985 (Philosophy of Space and Time by Hans Reichenbach. Translated by Maria Reichenbach and John Freund: witch introductory remarks by Rudolf Carnap. New York 1958)
- Эйнштейн А. Собрание научных трудов. В 4 т. Т.I. Работы по теории относительности 1905-1920; под редакцией И.Е. Тамма, Я.А. Смородинского, Б.Г. Кузнецова. – М.: НАУКА, 1965
