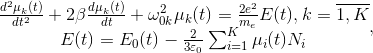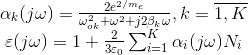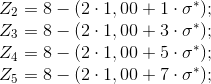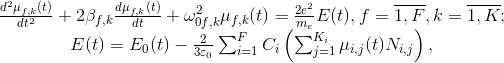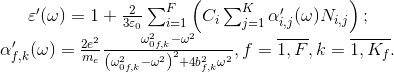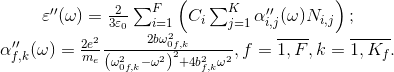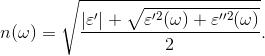Всякая керамика представляет собой в той или иной степени перспективный конструкционный материал. Таким образом, всестороннее исследование физических свойств любых представителей этого класса конденсированных сред, несмотря на тысячелетнюю историю использования керамики как таковой, остается актуальной проблемой, особенно с точки зрения технических наук.

Как известно, любой керамический диэлектрик является многокомпонентной системой, состоящей из кристаллической, стекловидной и газовой фаз вещества. При этом систематизировать общие характеристики электротехнических материалов данного класса по признаку «свойство» оказывается достаточно сложно, так как разнообразие их функциональных качеств не позволяет выявить минимальное количество общих признаков. Таким образом, наиболее распространенная классификация электротехнических керамик обычно проводится по признаку «состав», – например, корундовая, кварцевая, стеатитовая, кордиеритовая керамики и т.д. [1].

Корундовая керамика представляет собой высокоглиноземистые материалы, имеющие массовую долю оксида алюминия Al₂O₃ (корунда) – от 70 до 100 процентов. Например, к ней относятся промышленные образцы электрокерамик микролит, поликор, ГБ-7.

Химический состав промышленного образца композиционной электротехнической керамики, выбранный в качестве объекта проводимого исследования (таб. 1).

Таблица 1 – Химический состав исследуемого образца

Математическая модель упругой электронной поляризации любого отдельно взятого компонента корундовой керамики, представляющей собой композицию кристаллических оксидов, адекватно выражается системой уравнений вынужденных гармонических колебаний с трением [2]:

 (1)

где μ_k(t) – функции, описывающие изменения дипольных моментов электронных пар ионов (индекс k от 1 до 5 соответствует аниону кислорода, а другие – соединенному с ним катиону); K – общее число разновидностей электронных пар; β_k, ω_0k – коэффициенты затухания и частоты их собственных колебаний; e и m_e – заряд и масса электрона; E₀(t), E(t) – функции напряженности внешнего и эффективного полей; N_i – концентрации ионов; ε₀ – диэлектрическая проницаемость вакуума.

На основании выражений (1) вытекают непосредственно уравнения комплексной поляризуемости α_k(jω) электронных пар, а также кибернетическая модель комплексной диэлектрической проницаемости ε(jω) [3]:

. (2)

Динамические параметры рассматриваемых физических процессов в свою очередь могут быть определены аналитически с помощью следующих формул:

 (3)

где Q_k – эффективный заряд атомного остатка, влияющий на конкретную электронную пару; r_k – радиус ее орбитали; µ₀ – магнитная проницаемость вакуума; c – скорость света в вакууме; n_k – главное квантовое число орбитали; ћ – постоянная Планка.

Расчет эффективных зарядов может быть выполнен в рамках метода описания линейной комбинации атомных орбиталей Слэтера [4]. Сущность этого метода заключается в установлении постоянной экранирования σ*, позволяющей вычислить заряд атомного остатка, эффективно действующего на электроны произвольной оболочки частицы, с учетом эффекта экранизации ее атомного ядра внутренними электронами. Однако, методика описания слэтеровских атомных орбиталей изначально была сформирована исключительно для рассмотрения стационарных состояний атомов. Следовательно, обстоятельство появления полностью свободных предоптических оболочек в электронной конфигурации анионов обусловливает вероятность изменения типовых величин экранирующих вкладов их внешних электронов.

Для описания эффективных зарядов, влияющих на каждую из пар оптических электронов частицы кислорода со стороны его атомного остатка, предлагается использовать соотношения:

 (4)

где σ* – оптимизированное значение экранирующего вклада внешних электронов аниона, определяемое методом сканирования. В свою очередь алгоритм метода сканирования, используемого в данном случае для определения величин σ*, дающих возможность моделировать диэлектрические спектры кристаллов, практически адекватные их наблюдаемым поляризационным свойствам, состоит в реализации типового итерационного цикла.

После подбора подходящих значений экранирующего вклада оптических электронов анионов, выполненной на базе контрольных данных, соответствующих реальным диэлектрическим спектрам исследуемого материала в области видимых частот, должно быть достигнуто достаточно точное соответствие расчетных характеристик их экспериментальным аналогам.

Поскольку упругая электронная поляризация является аддитивным свойством вещества, не зависящим от его структуры и агрегатного состоя­ния, и складывается из поляризуемостей электронных оболочек отдельных ионов, исходная модель (1), трансформированная для кон­кретного керамического материала, может быть представлена в следующем общем вид:

 (5)

где F - общее число разновидностей композитов, составляющих керамиче­ский образец; С_i – их процентное содержание в материале.

На основании как системы уравнений (5) может быть получена вещественная частотная характеристика ком­плексной диэлектрической проницаемости композиционного материала, ко­торая будет описываться следующим набором выражений:

 (6)

В свою очередь мнимая частотная характеристика комплексной ди­электрической проницаемости композиционного материала может быть по­лучена с помощью выражений:

 (7)

Расчет оптического показателя преломления производится по формуле:

 (8)

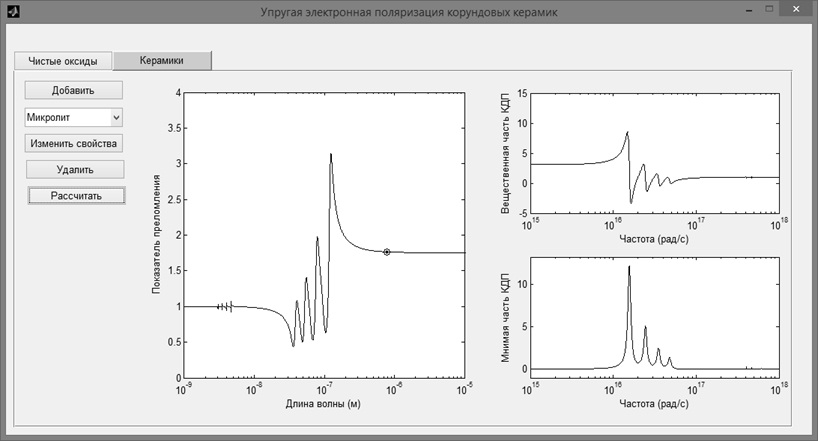
С целью проверки эффективности моделирования оптического показателя преломления n(ω) и частотных спектров вещественной и мнимой частей комплексной диэлектрической проницаемости εʹ(ω) и εʹʹ(ω) рассматриваемого промышленного образца корундовой керамики был проведен вычислительный эксперимент (рис. 1). 

Рисунок 1 – Расчетные спектры микролита

Оценим погрешность результатов расчета n(ω), полученных в рамках предлагаемой методики, сравнивая их численные значения с контрольными величинами для одного образца керамики. Полученные в итоге значения представлены в таблице 2.

Таблица 2 – Оценка погрешностей результата расчета

Таким образом, данная методика позволяет достаточно точно имитировать характеристики оптического показателя преломления и комплексной диэлектрической проницаемости корундовых керамик, имеющие место в области установления процессов их упругой электронной поляризации.

1. Диэлектрики и радиация. – В 8 кн. / под. общ. ред. Н.С. Костюкова. – М.: Наука, 2001-2008.
2. Еремин И.Е., Жилиндина О.В. Моделирование упругой электронной поляризации композиционных электрокерамик. I // Информатика и системы управления. – 2008. – № 1(15). – С. 28-38.
3. Еремин И.Е., Костюков Н.С. Построение модели процесса поляризации диэлектриков с помощью обратных связей // Информатика и системы управления. – 2001. – № 1. – С. 45-53.
4. Эткинс П. Кванты. Справочник концепций / пер. с англ. – М.: Мир, – 1977. – 496 с.

Все статьи автора «Мироненко Александр Михайлович»