Исходными данными для разработки алгоритмического и программного обеспечения являются:

• описание цифровых сигналов датчиков;
  
• описание алгоритмов формирования управляющих сигналов;
  
• математическая модель, реализованная в виде модели модуля SIMULINK программного комплекса MATLAB.

Исходными данными разработанных алгоритмов являются:

• описание сигналов датчиков, полученных посредством преобразования аналоговых сигналов с гексапода в цифровой вид с помощью аналогово-цифрового преобразователя.

Выходными данными разработанных алгоритмов являются:

• управляющие сигналы, преобразуемые в аналоговое представление посредством использования цифро-аналогового преобразователя;
• информационные сигналы вспомогательного и служебного характера.

Для реализации алгоритмов была выбрана аппаратная база: нейропроцессорные устройства на базе процессоров особого класса, 6-го поколения, широко используемые в настоящее время в военной и космической промышленности. Было выбрано семейство процессоров NeuroMatrix 640x, нейропроцессоры которого выпускаются научно-техническим центром “Модуль” (г.Москва) [3].

Выбор конкретных нейропроцессорных устройств предопределен заказчиком и преимуществами использования нейропроцессорных технологий [2]:

• высокий уровень распараллеливания (близкий к 100%);
• высокая энергоэффективность (меньше в тысячи раз относительно процессоров архитектуры фон-Неймана).

Практические исследования производились с использованием нейропроцессора NM6406 на базе инструментального модуля MC 51.03 и микрокомпьютера MB 77.07.     Эффективное распараллеливание вычислений достигается за счет аппаратной поддержки операции векторно-матричного умножения на нейропроцессоре NeuroMatrix NM6406. Все арифметические вычисления, относящиеся непосредственно к вычислению управляющих воздействий, производятся на векторном сопроцессоре. Так как векторный узел позволяет оперировать данными переменной разрядности, то для хранения входных данных и результатов вычислений удобно отводить по 32 разряда на целую и вещественную часть.

Для разработки алгоритмов и программного кода были реализованы подпрограммы следующих функциональных элементов математической модели специализированного вычислительного устройства (СВУ) управления гексаподом [7].

1. Матричный умножитель и матричный умножитель с накоплением.

Дифференциальные уравнения, описывающие динамику гексапода, могут быть представлены в виде разностных в векторно-матричной форме, которые удобны для реализации средствами вычислительной техники. Поэтому основная операция, которую должен выполнять СВУ – перемножение матриц, которые могут быть разбиты на пару элементарных операций «умножение – сложение» (умножение с накоплением). Для этой операции используется векторный сопроцессор, который представляет собой общий матричный узел для выполнения операций умножения с накоплением арифметических и логических операций, маскирования, функций активации над векторами и матрицами.

Это основной функциональный элемент с набором регистров общего назначения. Представляет собой матричную структуру 64х64, произвольно разделенную на столбцы и строки.

Структурная схема векторного сопроцессора приведена на рисунке 1.

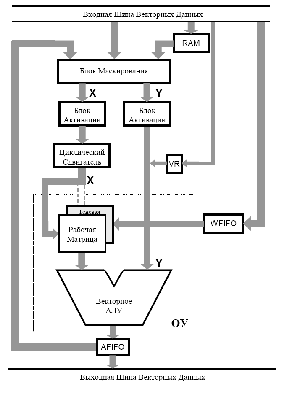
Рисунок 1. Структура векторного сопроцессора

Операция умножения с накоплением выполняется в рабочей матрице нейропроцессора:

,

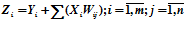где

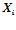 – элемент данных, поступающих на вход векторного сопроцессора;

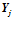– частичная сумма, накопленная на предыдущем этапе взвешенного суммирования или остаток после предыдущей операции;

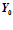 – элемент входного вектора данных;

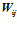 – весовой коэффициент, расположенный в соответствующей ячейке рабочей матрицы процессора;

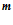 – количество столбцов рабочей матрицы процессора;

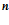 – количество строк рабочей матрицы процессора.

Рабочая матрица имеет 2 входа:

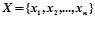- 64 разряда;

.

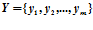Данные, полученные на входе 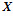 умножаются на ячейки матрицы, после чего они суммируются в пределах столбца, то есть в случае переполнения происходит потеря знаковых разрядом. Данные со входа  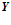поэлементно складываются с результатами умножения, выполненным над данными входа .

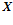Для выполнения операции взвешенного суммирования в рабочую матрицу предварительно загружаются весовые коэффициенты 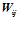. Это возможно двумя способами – либо непосредственно в рабочую матрицу, либо через теневую матрицу. Загрузка весовых коэффициентов через теневую матрицу наиболее эффективен, так как загрузка реализуется за один такт нейропроцессора. Теневая матрица существует в векторном узле нейропроцессора для ускорения работы, так как весовые коэффициенты загружаются в фоновом режиме за 32 такта. Перегрузка весовых коэффициентов из теневой в рабочую матрицу происходит за один такт.

Разбиение матрицы на строки определяется рабочим регистром 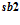. Он определяет предварительное разбиение 64-разрядных слов входных данных, поступающих на вход 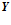. Разбиение рабочей матрицы на столбцы задаётся рабочим регистром 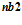. Этот же регистр определяет разбиение 64-разрядных данных на входе  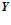и также предварительно заносится в виде слова данных в регистр. Этот же регистр определяет разрядность результатов вычисления, которые в итоге будут расположены в буферном регистре AFIFO. Таким образом, входные данные (операнды) и выходные значения упаковываются путем разбиения в 64-разрядные слова. Все операции в матрице производятся параллельно за 1 такт.

2.     Сумматор двух и более операндов.

Сумматор двух и более операндов реализован с использованием векторного блока процессора и операции взвешенного суммирования (рисунок 1) с пустым оператором умножения, то есть с “единичной” теневой и рабочей матрицей (все биты 64×32 заполнены единичными битами). Эффективность использования этой операции зависит от разрядности входных данных, так как за счет использования разбиения матрицы на строки и столбцы увеличивается скорость вычислений в связи с одновременной работой с несколькими операндами. Важной особенностью векторного процессора является реализация работы с операндами различной длины.

3.     Интегратор значений.

Для реализации операции интегрирования используются вычислительные методы, цель которых заменить операцию интегрирования на комплекс операций вида “сложение – умножение”. Алгоритма работы СВУ представлен на рисунке 2.

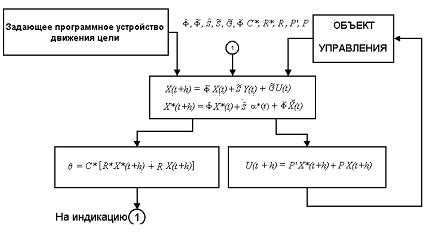
Рисунок 2. Алгоритм функционирования СВУ

На схеме приняты следующие обозначения: 

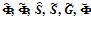— рабочие матрицы, полученные из матриц параметров гексапода и матриц параметров корректирующих фильтров;

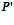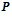, — матрицы параметров корректирующих связей (6×100);

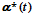— вектор-функция программы (18×1);

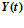 - вектор-функция наблюдения (сигналы, поступающие от измерительной системы) (30×1);

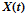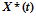, - вектор-функция текущего и программного состояния системы на i-м шаге управления (100×1);

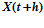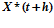,  - то же на (+1)-м шаге (100×1);

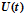 и 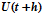 - вектор управляющих воздействий на -м и  ( + 1)-м шагах управления (30×1);

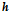 - шаг интегрирования (~0.001) ;

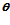 - значение отклонения фокальной оси гексапода от линии визирования объекта(3×1);

С*, R*, R — постоянные матрицы размерностью (3×3, 3×100, 3×100).

Из алгоритма управления гексаподом следует, что основной процедурой в СВУ является процедура умножения матрицы на вектор:

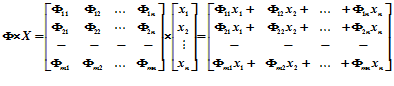
Одна компонента вектора результата получается суммированием произведения элементов строки матрицы на соответствующие элементы вектора - столбца. Эта последовательность операции повторяется столько раз, сколько строк в матрице. Для вычисления произведения матрицы на вектор необходимо выполнять 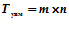 операций умножения, где  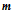 - число строк матрицы; 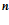- число столбцов и 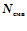_в операций сложения, определяемых по формуле: 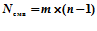операций сложения, или около 3000 пар операций “умножение - сложение”.

4.     Функции активации (насыщения).

Функции активации реализованы с использованием векторного блока процессора и операции взвешенного суммирования (рисунок 1). Реализованы подпрограммы двух типов функций активации: пороговая функция и функция насыщения. В блоках активации осуществляются вычисления над упакованными словами данных. Блоки активации позволяют применять функции активации ко всем элементам упакованного слова одновременно. Основную роль в управлении функциями активации играют регистры 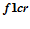 и 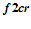. Блоки активации размещаются между устройством маскирования и рабочей матрицей или векторным вычислителем. Функции активации могут быть подвергнуты либо данные, поступающие на вход 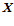, либо на 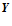, либо на оба входа сразу.

Пороговая активация реализована следующим образом.

Если значения битов данных, соответствующих битам “1″ регистра :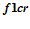

- равны, то поле данных не изменяется при обработке арифметической функцией активации (функцией насыщения);

- не равны и старший бит равен “0″, то значение заменяется на положительное пороговое;

- не равны и старший бит равен “1″, то значение заменяется на отрицательное пороговое.

Функция насыщения переводит неотрицательные значения элементов полей данных в “0″, отрицательные в “-1″.

Элементарные базовые операторы реализованы в виде макросов на языке нейроассемблера.

Результаты моделирования и анализа реализации программного кода СВУ на нейропроцессорной системе представлены на рисунке 3 [5,6].

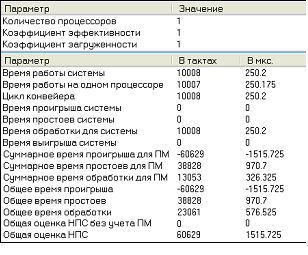
Рисунок 3. Результаты моделирования программного кода СВУ

Заключение.

В статье предложены специализированные алгоритмы матричных вычислений управляющих воздействий, коэффициентов регуляторов двигателей ног на примере гексапода и вычисления задаваемых и измеряемых перемещений с использованием концептуально новой вычислительной техники – нейропроцессора NM6406 на базе инструментального модуля MC 51.03 и микрокомпьютера MB 77.07, разрабатываемых НТЦ “Модуль”.

1. Vladimir Ruchkin, Vitaliy Romanchuk, Roman Sulitsa. Clustering, Restorability and Designing Of Embedded Computer System Based On Neuroprocessors // Proceedings of the 2nd Mediterranean Conference on Embedded Computing (MECO). – Budva, Montenegro, 2013. – С.58-62.
2. Галушкин А.И. Нейрокомпьютеры. Кн.3. М: ИПРЖР, 2000. 528 с.
3. НТЦ «Модуль»: сайт НТЦ «Модуль», 2011: URL: http:// http://www.module.ru.
4. Романчук В.А., Ручкин В.Н. Алгоритмы анализа вычислительных структур на базе нейропроцессоров // Вестник РГРТУ. – Рязань : РГРТУ, 2012. – №2. – Вып.40. – С.60–66.
5. Романчук В.А., Ручкин В.Н. Оценка результатов моделирования вычислительных систем на базе нейропроцессоров // Известия тульского государственного университета. Технические науки. – Тула : Издательство ТулГУ, 2013. – Вып.9. – Ч.2. – С.194-203.
6. Романчук В.А., Ручкин В.Н., Фулин В.А. Разработка модели сложной нейропроцессорной системы // Цифровая обработка сигналов. – Рязань : Информационные технологии, 2012. – №4. – С.70–74.
7. Ручкин В.Н., Романчук В.А., Фулин В.А. Когнитология и искусственный интеллект. – Рязань : Узорочье, 2012. – 260 с.
8. Романчук В.А., Лукашенко В.В. Разработка математической модели реструктуризуемого под классы задач, виртуализируемого кластера GRID-системы на базе нейропроцессоров // Вестник РГУ имени С.А.Есенина. – Рязань : РГУ имени С.А.Есенина, 2014. – №1(42). – C. 177- 182.
9. Романчук В.А., Ручкин В.Н. Разработка программного комплекса для моделирования и анализа нейропроцессорных систем обработки изображений // Цифровая обработка сигналов. – Рязань : Информационные технологии, 2010. – №1. – С.53–58.
10. Романчук В.А. Моделирование нейропроцессорных систем // Отраслевые аспекты технических наук : научно-практический журнал. – Москва : ИНГН, 2013. – №10(34). – С.19-24.

Все статьи автора «Романчук Виталий Александрович»