Уравнения в частных производных, описывающие процессы теплопроводности, диффузии и другие, неоднократно решаются на различных стадиях проектирования и эксплуатации современных сложных технических объектов. Например, при выполнении нейтронно-физического расчета (НФР) ядерного реактора с использованием разностных схем итерационно решается уравнение диффузии нейтронов [1, 2]

, (1)

где  – плотность потока нейтронов группы k в точке с координатой ;  – коэффициент диффузии нейтронов k-й группы;  – суммарное макросечение поглощения и рассеяния нейтронов группы k; К_эф– эффективный коэффициент размножения нейтронов;  – доля нейтронов группы k в нейтронах деления;  – макроскопическое сечение деления на нейтронах k-й группы;  – среднее число нейтронов деления на один поглощенный нейтрон;  – макроскопическое сечение рассеяния нейтронов группы l в группу k; М– количество энергетических групп нейтронов.

Многими исследователями при этом отмечались определенные фильтрующие свойства таких уравнений, состоящие, например, в том, что случайные, в основном высокочастотные, изменения свойств среды, описываемой данными уравнениями, приводят к появлению ярко выраженных низкочастотных гармонических составляющих в результатах расчета [3,4].

Исследования, проведенные автором настоящей статьи, показали, что в еще большей степени, чем само диффузионное уравнение процесса переноса нейтронов, похожими фильтрующими свойствами обладают групповые макроконстанты уравнения (1). В частности, серия расчетов, выполненных на одномерной модели реактора, позволила установить, что при использовании для НФР макроконстант, отфильтрованных цифровым фильтром нижних частот (рис.1) с заданной частотой среза , получается поле нейтронов, в котором практически отсутствуют гармонические составляющие выше . Рассмотренный в работе одномерный случай не снижает общности изложения, а лишь повышает наглядность проведенных расчетов.

Рис 1. Амплитудно-частотная характеристика  цифрового фильтра нижних частот, использованного для фильтрации макроконстант диффузионного уравнения:
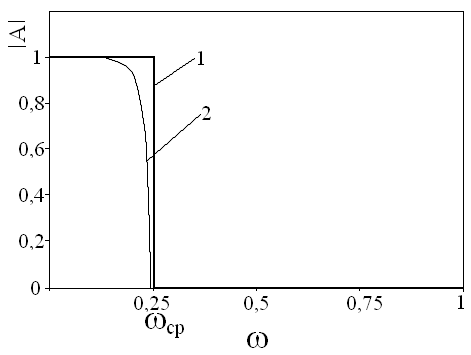
1- идеальный ФНЧ; 2- реальный ФНЧ.

При выполнении цифровой фильтрации макроконстант учитывалось, что они представляют собой обычные числовые последовательности конечной длины. Например, в каждом i-м узле расчетной сетки известно макроскопическое сечение деления . В совокупности для всех узлов сетки значения  образуют одномерный массив – он обрабатывался фильтром нижних частот с заданной частотой среза . При этом цифровой фильтр должен вносить как можно меньшую погрешность в обрабатываемые данные, для чего его расчет должен быть выполнен с высокой точностью с тем, чтобы погрешность цифровой фильтрации не превышала 0,1%. Аналогично формировались и обрабатывались массивы для всех остальных макроконстант уравнения (1).

Таким образом, при фильтрации, то есть сглаживании, макроконстант среды устраняются высокочастотные составляющие поля нейтронов, то есть фактически получается только его макроход. Этот результат является принципиально важным, так как позволяет корректно и быстро рассчитать макрополе нейтронов на грубой сетке и по-новому организовать нейтронно-физический расчет, значительно сократив общее число итераций и время счета.

1. Филипчук Е.В., Потапенко П.Т., Постников В.В. Управление нейтронным полем ядерного реактора. М.: Энергоиздат, 1981.
2. Доллежаль Н.А., Емельянов И.Я. Канальный ядерный энергетический реактор. М.: Атомиздат, 1980.
3. Карпов В.А., Назарян В.Г., Постников В.В. Исследование случайной составляющей распределения тепловыделения в ядерном реакторе. – Атомная энергия, 1976, т. 40, вып. 6, с. 456-460.
4. Горюнов В.К. Перекосы поля нейтронов в реакторах при случайно распределенных возмущениях макросечений. – Атомная энергия, 1980, т. 49,   вып. 5, с. 321–323.

Все статьи автора «Саманчук Владимир Никифорович»