Долговечность, надежность и экономичность работы двигателя внутреннего сгорания (ДВС) во многом зависят от качества моторного масла. Основным назначением моторного масла является: снижение коэффициента трения и износа трущихся сопряжений, отвод тепла, вынос продуктов износа из зоны трения, повышение герметичности рабочих полостей двигателя, защита от коррозии и т.д. 
Для обеспечения всех перечисленных функций моторное масло должно обладать определенными свойствами. Поэтому к моторному маслу предъявляется ряд эксплуатационных требований, степень удовлетворения которым зависит от физико-химических параметров (ФХП) моторного масла.
Моторное масло в ДВС работает в крайне жестких условиях, которые оказывают на него деструктивное воздействие. В результате этих воздействий физико-химические параметры моторного масла изменяются, в результате чего эксплуатационные свойства снижаются и при достижении определенных значений ФХП масло полежит замене. 
Заводы-изготовители назначают периодичность замены моторных масел без учета их реального состояния. Так, для магистральных автомобилей КАМАЗ установлена следующая периодичность замены моторного масла: группы CF- 4 и выше через каждые 30000 км; в двигателе автомобиля Волжского автомобильного завода Лада – Калина следует заменять через 15 тыс. км пробега. 
При этом часто заменяются масла, не потерявшие своего качества. В других случаях наоборот, техника работает на маслах, утративших свои физико-химические и эксплуатационные свойства. Недостатком такой системы является повышенный расход масла, достигающий 50% и выше расходов на эксплуатацию автотранспортных средств, а также снижение их технической надежности.
Многие отечественные и зарубежные специалисты считают необходимым пересмотреть сроки службы моторных масел. Но научно-обоснованных критериев, позволяющих нормировать эту продолжительность, пока нет. Поэтому в эксплуатации придерживаются норм, рекомендованных разработчиками машин и оборудования. То есть норм, которые не учитывают реальную работоспособность и фактическое состояние смазочных материалов.
В практике эксплуатации автомобильного парка на некоторых автотранспортных предприятиях для анализа качества работающего моторного масла применяются различные методы экспресс-анализа, у которых один общий недостаток: контроль качества осуществляется по отдельным, немногочисленным параметрам моторного масла. При этом отсутствует полная картина состояния и остаточного ресурса масла. 
Поэтому разработка методики определения остаточного ресурса работающего моторного масла является актуальной задачей. В силу этого разработка математической модели процесса старения моторного масла представляет определенную научную и практическую значимость.
В рассматриваемой проблеме моделью является работающее моторное масло и его физико-химические параметры, а математической моделью – система математических соотношений, описывающих процесс старения моторного масла 
Для разработки математической модели старения работающего моторного масла были использованы результаты исследования изменения физико-химических показателей моторного масла от величины пробега автомобиля. Исследования проводились в автохозяйстве предприятия «ХиммашТранспорт» г. Пензы. Парк автомобилей составляли седельные тягачи марки IVECO, исследованию подвергалось масло LiquMoli.
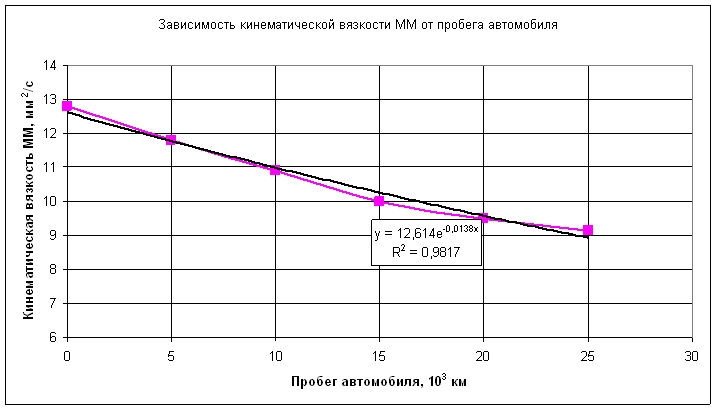
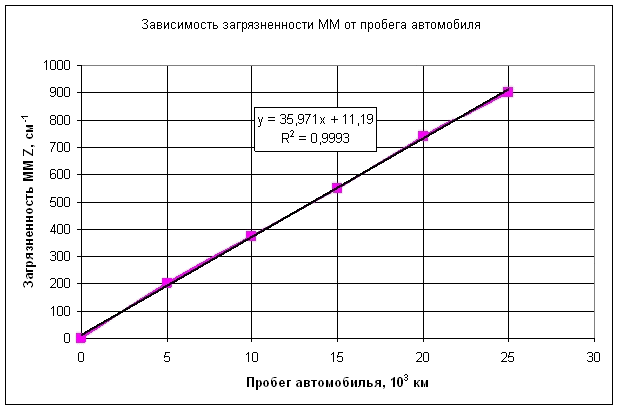
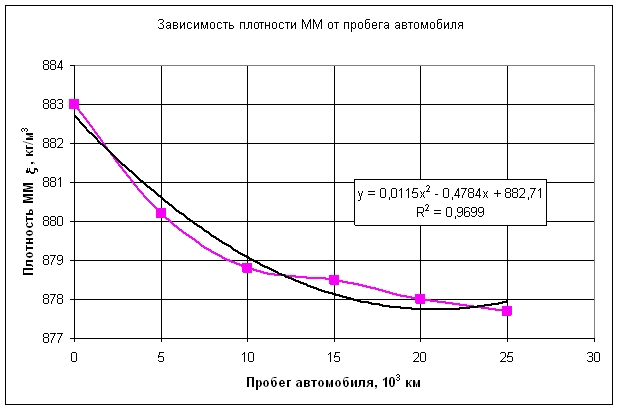
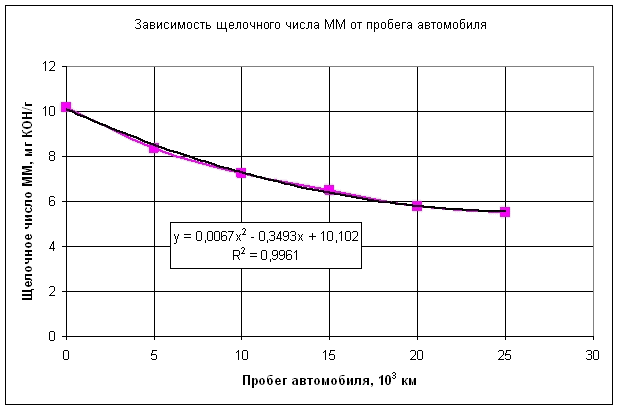
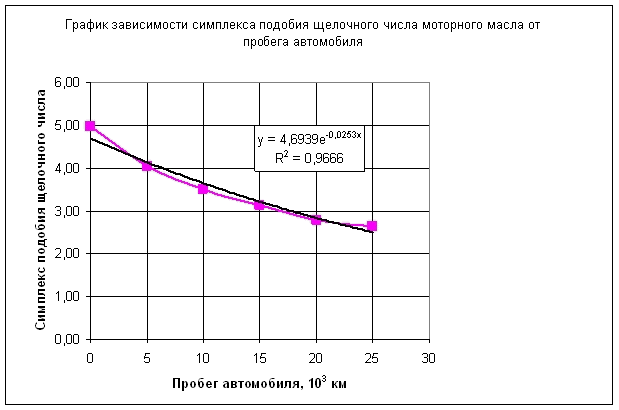
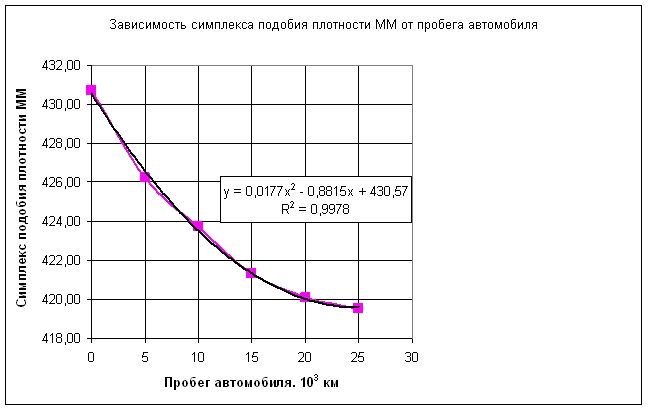
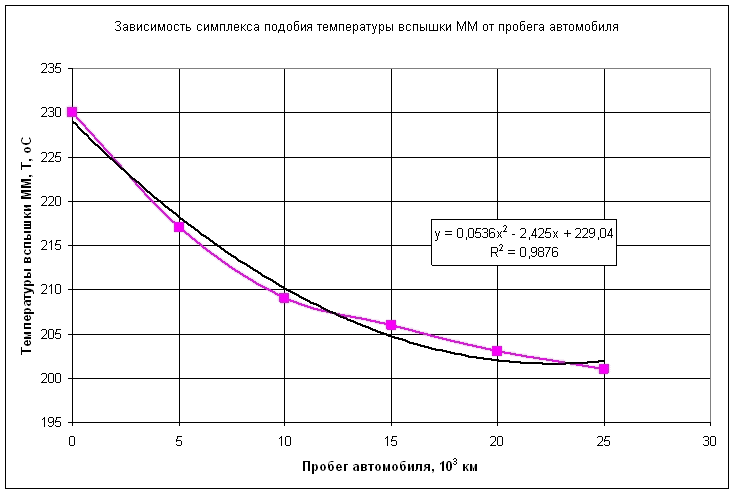
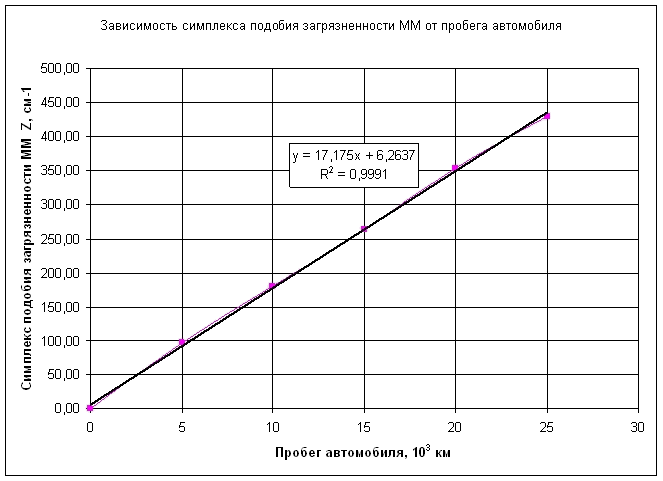
Физико-химические показатели моторного масла определялись по стандартным методикам. Графики зависимостей показателей качества моторного масла от пробега автомобиля представлены на рис. 1-6

Рис. 1 Зависимость кинематической вязкости моторного масла при температуре 100 оС от пробега автомобиля	Рис. 2 Зависимость диэлектрической проницаемости моторного масла от пробега автомобиля
Рис. 3 Зависимость загрязненности моторного масла от пробега автомобиля	Рис. 4 Зависимость плотности моторного масла от пробега автомобиля
Рис. 5 Зависимость температуры вспышки моторного масла от пробега автомобиля	Рис. 6 Зависимость щелочного числа моторного масла от пробега автомобиля

Из анализа графиков рис. 1-6 следует, что между физико-химическими показателями моторного масла существует корреляционная связь. Наличие корреляционной связи между характеристиками моторного масла подтверждается и в ряде других работ [1]. 
Наличие корреляционной связи между ФХП моторного масла дает возможность, используя теорию подобия [2], по измеренным значениям одного параметра определять состояние моторного масла в зависимости от пробега автомобиля.
Согласно теории подобия, связь между определяемой переменной Yi и определяющей переменной Y определяется выражением:

 (1)

где: К_Yi – коэффициент подобия.
Если известны переменные Yi и Y , то коэффициент подобия К_Yi определяется выражением:

 (2)

Из анализа графиков 1-6 видно, что законы изменения физико-химических параметров моторного масла от величины пробега автомобиля не являются линейными. Поэтому коэффициент подобия К_Yi удобно представлять в виде графика К_Yi= f(Д) как функцию от дальности пробега автомобиля. 
Т.к. физико-химические параметры моторного масла имеют разную размерность, то и коэффициент подобия К_Yi не будет безразмерным. Размерный коэффициент К_Yi в теории подобия называется симплексом подобия.
В качестве определяющей величины для разработки математической модели примем диэлектрическую проницаемость моторного масла ?. Следует отметить, что диэлектрическая проницаемость есть величина безразмерная, поэтому симплексы подобия для определяемых физико-химических параметров моторного масла будут иметь соответствующую им размерность.
Расчетные значения симплексов подобия для физико-химических параметров моторного масла представлены в табл. 1 .
Таблица 1 Расчетные значения симплексов подобия ФХП моторного масла

Пробег автомобиля Д, 103 км	0	5	10	15	20	25
Диэлектрическая проницаемость, ?	2,05	2,065	2,074	2,085	2,09	2,092
- симплекс подобия щелочного числа, мг КОН/г	4,98	4	3,5	3,12	2,78	2,63
- cимплекс подобия плотности моторного масла, кг/м3	430,73	426,25	423,72	421,34	420,1	419,55
- cимплекс подобия оптической плотности моторного масла	0,454	0,266	0,145	0,062	0,024	0,005
- cимплекс подобия температуры вспышки моторного масла, оС	112,2	105,08	100,77	98,8	97,13	96,08
- симплекс подобия загрязненности моторного масла	0	96,85	180,81	263,79	354,07	430,21
- симплекс подобия кинематической вязкости моторного масла при температуре 100 оС	6,24	5,71	5,26	4,8	4,55	4,37

По расчетным значениям симплексов подобия были построены соответствующие графики. Обработка расчетных значений производилась с применением пакета прикладных программ для решения задач и технических вычислений Exel.
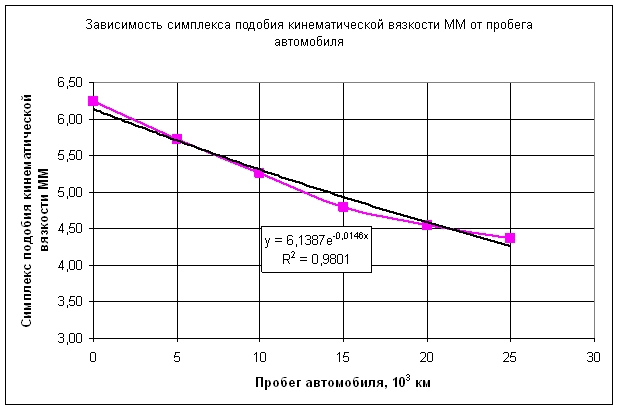
Графики симплексов подобия в функции дальности пробега автомобиля приведены на рис. 7-12.

Рис. 7 Зависимость симплекса подобия щелочного числа от пробега автомобиля	Рис. 8 Зависимость симплекса подобия плотности моторного масла от пробега автомобиля
Рис. 9 Зависимость симплекса подобия оптической плотности моторного масла от пробега автомобиля	Рис. 10 Зависимость симплекса подобия температуры вспышки моторного масла от пробега автомобиля
Рис. 11 Зависимость симплекса подобия загрязненности моторного масла от пробега автомобиля	Рис. 12 Зависимость симплекса подобия кинематической вязкости моторного масла от пробега автомобиля

Уравнения кривых симплексов подобия имеют вид:

- для кинематической вязкости ММ:
- для температуры вспышки ММ:
- для загрязненности ММ:
- для щелочного числа ММ:
- для плотности ММ:
- для оптической плотности ММ:

Приведенные выше уравнения являются математической моделью процесса старения моторного масла в зависимости от пробега автомобиля, т.к. дают возможность определить текущее состояние моторного масла по определенным показателям его работоспособности в зависимости от пробега автомобиля. Физико-химические параметры моторного масла определяются как произведение соответствующего симплекса подобия К_yi на величину измеренного значения диэлектрической проницаемости ? для фиксированного значения пробега автомобиля на момент тестирования моторного масла.
Пример расчета кинематической вязкости моторного масла.
Определить кинематическую вязкость моторного масла, если:
- пробег автомобиля составляет 7500 км;
- измеренное значение диэлектрической проницаемости моторного масла ? = 2,07.

Рис. 13 Алгоритм расчета физико-химических параметров моторного масла

Решение.
1. По графику симплекса подобия кинематической вязкости моторного масла К_? = f(L) определить значение К_? для пробега 7500 км: К_? =5,5;
2. Измеренное значение диэлектрической проницаемости моторного масла ? = 2,07 при пробеге автомобиля 7500 км;
3. Определить значение кинематической вязкости моторного масла при 100 ^оС по формуле:
ν = К_ν · ? = 5,5 ·2,07 = 11,385 мм²/с;
4. Сделать соответствующий вывод о запасе ресурса моторного масла по вязкости и необходимости его замены.
Алгоритм расчета физико-химических параметров моторного масла по предлагаемой методике с применением пакета прикладных программ для решения задач и технических вычислений Matlab и Exel приведен на рис. 13.
В сравнении с методами ГОСТ применение разработанной математической модели позволит значительно снизить трудоемкость, сократить время и упростить определение показателей качества моторного масла. А значит можно организовать мониторинг качества моторного масла в процессе эксплуатации транспортных средств и производить замену моторного масла по фактическому состоянию.

1. Долгова, Л.А.,  Обеспечение рационального ресурса моторного масла в двигателях [Текст] / Л.А. Долгова, В.В. Салмин // Вестник Чувашского государственного педагогического университета им. И.Я. Яковлева. – 2012. – № 2-1. –С. 46-56.
2. Веников, В.А. Теория подобия и моделирования.  Учебное пособие для вузов [Текст] / В.А. Веников. – 2-е изд., доп. и перераб., 1976. – 479 с.
3. Исследование изнашивания прецизионных деталей дизельной топливной аппаратуры [Текст] / А.В. Новичков, Е.В.Новиков, Е.Г. Рылякин, А.В. Лахно, П.И. Аношкин // Международный научный журнал. – 2014. – № 3. – С. 108-111.

Все статьи автора «Долгова Лариса Александровна»