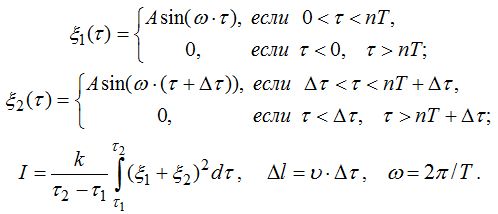Введение
Изучение основ физической науки, повышение качества физического образования требует модернизации преподавания физики, освоения методологии научного познания, совершенствования методики изучения отдельных вопросов [4, с. 8–57]. Определенный интерес при изучении интерференции световых волн представляет собой вопрос о временной когерентности [5, с. 199–276]. Как известно, свет излучается при переходе атомов из возбужденного состояния в основное. При этом образуются цуги световых волн, которые можно упрощенно представить в виде “обрывков” гармонических волн, имеющих определенную пространственную и временную протяженность. Результат интерференции во многом зависит от того, будет ли разность хода превышать длину цуга, пройдут ли цуги точку наблюдения в перекрывающиеся промежутки времени или нет. В настоящей статье обсуждается один из вариантов методики экспериментального и теоретического изучения интерференции цугов. Она может включать в себя использование компьютерной программы, моделирующей это явление и позволяющей рассчитать интенсивность в точке наблюдения при различных разностях хода для цугов различной длины.
Обсуждая интерференцию волновых цугов, обычно говорят о когерентных волнах, длине и времени когерентности. Когерентными называются волны, которые способны интерферировать. Вообще, когерентность –– это “коррелированное протекание во времени и пространстве нескольких случайных колебательных или волновых процессов, позволяющее получить при их сложении четкую интерференционную картину” [6, с. 394–396]. Минимальная задержка между волнами, приходящими в некоторую точку наблюдения, при которой они уже не интерферируют, называется временем когерентности. Если волны представляют собой “обрывки” синусоид, то время когерентности примерно равно длительности цуга t_к, а длина когерентности –– длине цуга L_к=v* t_к.
1. Качественное объяснение интерференции цугов
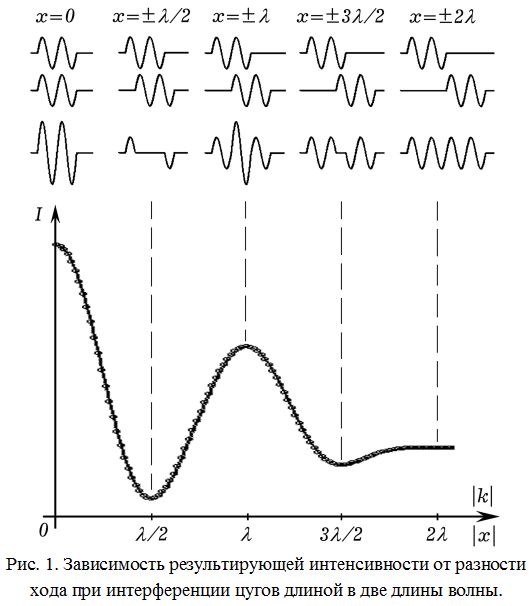
Допустим, два источника периодически излучают цуги одинаковой частоты, длина L_к которых равна двум длинам волн. Считая, что в точку наблюдения волны приходят с одинаковыми амплитудами, рассчитаем зависимость результирующей интенсивности I от разности хода x. Цуги, приходящие в точку наблюдения, результат их суперпозиции при различных разностях хода x, а также график зависимости I(x), полученный методом компьютерного моделирования, представлены на рис. 1.
При разности хода x=0 цуги достигают точки наблюдения одновременно и в фазе, поэтому усиливают друг друга и создают максимум нулевого порядка (k=0). Когда разность хода x равна половине длины волны (k равно 1 или –1), цуги практически полностью гасят друг друга, в результате наблюдается минимум. Нескомпенсированными остаются только две крайние полуволны, поэтому результирующая интенсивность близка, но не равна нулю. Если разность хода x равна длине волны, то перекрывающиеся части цугов усиливают друг друга (k=2) и наблюдается максимум. Однако, так как цуги приходят в точку наблюдения не одновременно, то они перекрываются не полностью, поэтому результирующая интенсивность меньше, чем в центральном максимуме. Если разность хода x равна 1,5 длин волн (k=3), то наблюдается минимум, в котором результирующая интенсивность больше, чем в первом минимуме.
При разности хода x, равной или превышающей длину когерентности L_к, цуги проходят точку наблюдения в неперекрывающиеся интервалы времени, поэтому результирующая интенсивность равна сумме интенсивностей каждой волны по отдельности и интерференция не наблюдается. Таким образом, интерференция наблюдается тогда, когда разность хода x меньше длины когерентности L_к, при этом число минимумов интенсивности равно удвоенному числу длин волн в цуге.
2. Компьютерная модель интерференции цугов
Пусть два источника периодически и одновременно излучают цуги волн длительностью t_к, которые имеют равные частоты f = 1/T. Рассчитаем интенсивность в точке наблюдения при различных разностях хода x и изучим зависимость результата интерференции от длины когерентности L_к [3, с. 71]. Результирующее колебание в соответствии с принципом суперпозиции равно сумме складываемых колебаний. Средняя интенсивность пропорциональна интегралу от квадрата смещения частиц среды в точке наблюдения за время, много большее периода испускания цугов, отнесенное к этому времени. Длину когерентности L_к можно найти, как произведение длительности цуга (то есть времени когерентности) на скорость волны. Если число длин волн в цуге обозначить через n, то получим следующие формулы:
Алгоритм построения графика зависимости интенсивности при интерференции цугов волн от разности хода состоит в следующем: 1) задается разность хода x; 2) вычисляется средняя интенсивность I, для этого складываются колебания, создаваемые источниками в точке наблюдения при заданной разности хода x, результат возводится в квадрат и интегрируется по времени; 3) на координатной плоскости “интенсивность–разность хода” ставится точка; 4) разность хода x увеличивается на небольшую величину, после чего компьютер переходит к операции 2. Численное интегрирование осуществляется методом прямоугольников или трапеций, которые подробно рассмотрены в [1].
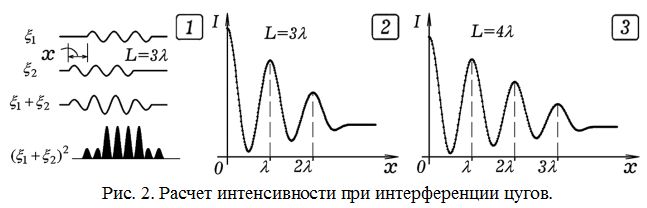
Используется программа 1. Получающиеся графики зависимости интенсивности I от разности хода x для цугов, длина L_к которых равна трем и четырем длинам волн, изображены на рис. 2. Анализируя рис. 1 и 2, можно обнаружить, что число минимумов интенсивности, наблюдаемых при интерференции цугов, равно удвоенному числу длин волн в цуге.
3. Экспериментальное изучение интерференции звуковых цугов.
Рассмотрим методику экспериментального изучения интерференции звуковых цугов и введения понятия временной когерентности, разработанную в учебно–исследовательской лаборатории “Учебный физический эксперимент” Глазовского государственного педагогического института под руководством профессора В.В.Майера. Она подробно описана в диссертации “Методика учебного фундаментального эксперимента по волновой физике” [2, c. 125–133], которую можно скачать с сайта http://maier-rv.glazov.net .
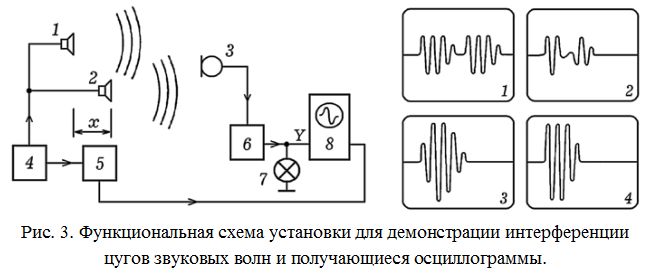
Для демонстрации зависимости результата интерференции от степени временной когерентности волн используется экспериментальная установка, изображенная на рис. 3. Одинаковые динамики 1 и 2 соединены с одним из выходов генератора звуковых цугов 4, к другому выходу которого подключено устройство задержки 5, соединенное с входом запуска ждущей развертки осциллографа 8. Приемником звука служит микрофон 3, соединенный с входом усилителя 6, выход которого подключен к лампочке накаливания 7 и входу Y осциллографа. Один из динамиков закреплен в штативе, а другой держат в руке. Для измерения разности хода волн применяется линейка. Принципиальные схемы генератора звуковых цугов и устройства задержки представлены в приложении к диссертации [2, c. 230–233].
Установка функционирует следующим образом. Генератор звуковых цугов периодически вырабатывает последовательности из нескольких электрических колебаний, преобразуемых динамиками в звуковые цуги, и одновременно формирует импульс, поступающий на устройство задержки. Через регулируемый промежуток времени устройство задержки выдает электрический импульс, запускающий ждущую развертку осциллографа. В результате на экране высвечивается осциллограмма усиленного сигнала с выхода микрофона. Так как частота следования генерируемых цугов, равная частоте запуска развертки, достаточно велика, то глаз, в силу своей инерционности, воспринимает осциллограмму как неподвижную. Для индикации среднего значения интенсивности волны в точке, где находится микрофон, используется подключенная к выходу усилителя лампочка накаливания или вольтметр.
С помощью переключателя переводят генератор звуковых цугов в режим непрерывных колебаний. Динамики включают в фазе и устанавливают их рядом друг с другом на одинаковых расстояниях от микрофона. При этом наблюдается яркое свечение индикаторной лампочки, амплитуда синусоидальной осциллограммы достигает максимума. Приближая или удаляя от микрофона динамик 2, последовательно проходят чередующиеся минимумы и максимумы, демонстрируя периодическое изменение яркости свечения лампочки и амплитуды синусоиды на экране. При этом во всех максимумах лампочка горит в полный накал, а во всех минимумах –– практически не горит. Таким образом, при наложении двух гармонических волн, имеющих равные частоты, независимо от разности хода между ними происходит интерференция; такие волны являются когерентными.
Переключают генератор звуковых цугов в режим, в котором он выдает цуги длиной, например, в три или пять длин волн. Отодвигают подвижный динамик от неподвижного настолько, чтобы на экране были отдельно видны осциллограммы цугов, излучаемых каждым источником звука. Уменьшают расстояние между динамиками и демонстрируют, что пока разность хода x превышает длину цуга L_к (то есть время запаздывания одного цуга относительно другого превосходит их длительность t_к), цуги через точку наблюдения следуют один за другим, и яркость лампочки не меняется. В этом случае результирующая интенсивность в точке, где находится микрофон, равна сумме интенсивностей накладывающихся волн, то есть интерференция отсутствует.
Приближая подвижный динамик к неподвижному, показывают, что когда разность хода между волнами становится меньше длины цугов, результирующая интенсивность начинает изменяться от максимального до минимального значений, причем максимумы становятся все более высокими, а минимумы –– более глубокими. На экране осциллографа наблюдается, как один цуг частично накладывается на второй, давая при этом минимум, максимум или промежуточное значение амплитуды. Получающиеся осциллограммы изображены на рис. 3 справа. Когда разность хода становится близкой к нулю, в минимумах лампочка полностью гаснет. Если оба цуга приходят к микрофону одновременно и в фазе, они полностью накладываются и взаимно усиливают друг друга, лампочка горит с максимальной яркостью. Это происходит в случае, когда динамики равноудалены от микрофона, а их диффузоры колеблются синфазно. Рассмотренный эксперимент убедительно доказывает, что результат интерференции реальных волн зависит не только от разности хода, но и от длины составляющих их цугов, и позволяет ввести понятие временной когерентности волн.
Заключение
В статье рассмотрен один из возможных вариантов методики изучения интерференции цугов и введения понятия временной когерентности. Он предполагает проведение учебного эксперимента со звуковыми цугами и использование компьютерной модели, позволяющей рассчитать и построить график зависимости результирующей интенсивности в точке наблюдения от разности хода для цугов различной длины. Использование натурного и вычислительного экспериментов позволяет убедительно доказать, что: 1) при наложении цугов волн интерференция происходит тогда, когда цуги проходят точку наблюдения в перекрывающиеся промежутки времени; 2) чем больше длительность и пространственная протяженность цуга (время и длина когерентности), тем больше разность хода волн, при которых они еще интерферируют; 3) число минимумов интенсивности, наблюдаемых при интерференции цугов, равно удвоенному числу длин волн в цуге.
Библиографический список
- Кунин С. Вычислительная физика. –– М.: Мир, 1992. –– 518 с.
- Майер Р.В. Методика учебного фундаментального эксперимента по волновой физике: Дисс. … канд. пед. наук. М., 1995. –– 258 с.
- Майер Р.В. Компьютерное моделирование физических явлений. –– Глазов, ГГПИ: 2009. –– 112 с.
- Разумовский В.Г., Майер В.В. Физика в школе. Научный метод познания и обучение. –– М.: Гуманитар. изд. центр ВЛАДОС, 2004. –– 463 с.
- Сивухин Д.В. Общий курс физики. Учеб. пособие: Для вузов. В 5 т. Т. IV. Оптика. –– М.: Физматлит, 2005. –– 792 с.
- Физическая энциклопедия. Т 2. // Под ред. А.М.Прохорова. –– Москва, Советская энциклопедия, 1990. –– 703 с.